标签:code math nal max 聚类 image https 结构 matrix

在机器学习领域,语言识别和图像识别都比较容易做到。语音识别的输入数据可以是音频频谱序列向量所构成的matrix,图像识别的输入数据是像素点向量构成的矩阵。但是文本是一种抽象的东西,显然不能直接把文本数据喂给机器当做输入,因此这里就需要对文本数据进行处理。
现在,有这么一个有趣的例子,我接下来要讲的模型就可以做到。
从我们人的角度来看,Paris是法国的首都,那么首都减去国家再加上一个国家,很可能表示的就是另一个国家的首都。因此这里的结果就是华盛顿Washington.机器想做到这一点,并不容易。
众所周知,只有标量或者向量可以应用加减法,抽象的自然语言该如何做到呢?
一个很自然的想法就是,自然语言能否表示成数学的形式,这样就可以更加方便地研究其规律了。
答案是肯定的。
现在我们可以进行思考,如何将文本中的词语用数学的形式表达出来,也就是说,文本中藏着哪些数学形式需要我们去挖掘。
文本中各个词语出现的频数是有限的,这是一个可以提取的数学形式
从逻辑的角度出发,词语之间不可能是独立的,一个词语的出现肯定与另一个或者若干个词语有关系。这就涉及到词语共现的层面了。
统计语言模型和大多数的词向量表示都是基于以上两点考虑的。
词向量的表现形式主要分为两种,一种是one-hot(one-hot representation)表示方式,将词表示成一个很长的向量,向量的长度就是词典的长度;另一种表示方法是分布式表示(distributed representation).同时,分布式表示方法又可以分为基于矩阵的表示方法、基于聚类的表示方法和基于神经网络的表示方法。
首先,最简单的就是one-hot表示方法,将词表示成一个很长的向量,向量的分量只有一个1,其他全为0,1所对应的位置就是该词在词汇表中的索引。
这样表示有两个缺点:
容易受维度灾难(the curse of dimentionality)的困扰;
没有考虑到词之间的关系(similarity)。
现在主要应用的都是分布式表示形式了。下面介绍一种简单的分布式表示形式——基于矩阵的表示形式。
如下表所示:
| Probability and Ratio | k = solid | k = gas | k = water | k = fashion |
|---|---|---|---|---|
| \(p(k\vert ice)\) | \(1.9\times 10^{-4}\) | \(6.6\times 10^{-5}\) | \(3.0\times 10^{-3}\) | \(1.7\times 10^{-5}\) |
| \(p(k\vert steam\)) | \(2.2\times 10^{-5}\) | \(7.8\times 10^{-4}\) | \(2.2\times 10^{-3}\) | \(1.8\times 10^{-5}\) |
| \(p(k\vert ice)/(p(k\vert steam)\) | \(8.9\) | \(8.5\times 10^{-2}\) | \(1.36\) | \(0.96\) |
简单说一下上面的矩阵。
假设我们对一些热力学短语或者词语的概念感兴趣,我们选择i=ice,k=steam,我们想看看ice和steam的关系,可以通过他们与其他词语的共现频率来研究。这些其他词语我们称之为探测词。这里我们选择探测词k为solid,gas,water和fashion。显然,ice与solid的相关性较高,但是与steam相关性较低,因此我们期望看到的是\(p_{ik}/p_{jk}\)比值比较大。对于探测词gas,我们期望看到的是\(p_{ik}/p_{jk}\)比值比较小。而water和fashion与ice和steam的关系要么都十分密切,要么都不怎么密切,因此对于这两个探测词,\(p_{ik}/p_{jk}\)应该接近于1.
上表是基于一个很大的语料库统计得出的,符合我们的预期。相比于单独使用原始概率,概率比值可以更好的区分相关词语和不相关词语,比如solid和gas与water和fashion;也可以很容易区分两个相关词。
那么,在正式介绍自然语言处理,或者说wrod2vec之前,有必要介绍以下统计语言模型。它是现在所有语言模型的基础。
第二个需要讲的分布式表示方式是基于神经网络的表示方法。在此之前,有必要讲一下传统的统计语言模型,毕竟它对语言模型影响深远。
给出以下三个句子:
美联储主席本·伯南克昨天告诉媒体7000亿美元的救助资金将借给上百家银行、保险公司和汽车公司
美主席联储本·伯南克告诉昨天媒体7000亿美元的资金救助将借给百上家银行、保险公司和汽公车司
美主车席联储本·克告诉昨天公司媒体7000伯南亿美行元的金将借给百救助上家资银、保险公司和汽对于第一个句子,语句通畅,意思也很不明白;对于第二个句子,虽然个别词语调换了位置,但也不影响阅读,我们仍然能够知道表达的是什么意思;对于第三个句子,我们就很难知道具体表示什么意思了。
如果问你为什么第三个句子不知道表达什么,你可能会说句子混乱,语义不清晰。在上个世纪70年代的时候,科学家们也是这样想的,并且试图让计算机去判断一个句子的语义是否清晰,然而,这样的方法是走不通的。
贾里尼克想到了一种很好的统计模型来解决上述问题。判断一个句子是否合理,只需要看它在所有句子中出现的概率就行了。第一个句子出现的概率大概是\(10^{-20}\),第二个句子出现的概率大概是\(10^{-25}\),第三个句子出现的概率大概是\(10^{-70}\),第一个句子出现的可能性最大,因此这个句子最为合理。
那么,如何计算一个句子出现的概率呢,我们可以把有史以来人类说过的话都统计一遍,这样就能很方便的计算概率了。然而,你我都知道这条路走不通。
假设想知道S在文本中出现的可能性,也就是数学上所说的S的概率,既然\(S=w_1,w_2,...,w_n\),那么不妨把S展开表示,
\[P(S)=P(w_1,w_2,...,w_n)\]
利用条件概率的公式,S这个序列出现的概率等于每一个词出现的条件概率的乘乘积,展开为:
\[P(w_1,w_2,...,w_n)=P(w_1)P(w_2\vert w_1)P(w_3\vert w_1,w_2)\cdots P(w_n\vert w_1,w_2,\cdots w_{n-1})\],
计算\(P(w_1)\)很容易,\(P(w_2\vert w_1)\)也还能算出来,\(P(w_3\vert w_1,w_2)\)已经非常难以计算了。
假设上面的n不取很长,而只取2个,那么就可以大大减少计算量。即在此时,假设一个词\(w_i\)出现的概率只与它前面的\(w_{i-1}\)有关,这种假设称为1阶马尔科夫假设。
现在,S的概率就变得简单了:
\[P(w_1,w_2,...,w_n) \approx P(w_1)P(w_2\vert w_1)\]
那么,接下来的问题就变成了估计条件概率\(P(w_i\vert w_{i-1})\),根据它的定义,
\[P(w_i\vert w_{i-1}) = \frac{P(w_i,w_{i-1})}{P(w_{i-1})}\],
当样本量很大的时候,基于大数定律,一个短语或者词语出现的概率可以用其频率来表示,即
\[P(w_i,w_{i-1}) \approx \frac{count(w_i,w_{i-1})}{count(*)}\]
\[P(w_{i-1}) \approx \frac{count(w_{i-1})}{count(*)}\]
其中,\(count(i)\)表示词\(i\)出现的次数,\(count\)表示语料库的大小。
那么
\[P(w_i\vert w_{i-1}) = \frac{P(w_i,w_{i-1})}{P(w_{i-1})} \approx \frac{count(w_i,w_{i-1})}{count(w_{i-1})}\]
在前面的模型中,每个词只与前面1个词有关,和更前面的词就没有关系了,这似乎简单的有点过头了。那么,假定每个词\(w_i\)都与前面的N-1个词有关,而与更前面的词无关,这样,当前词的概率只取决于前面N-1个词的联合概率,即
\[P(w_1\vert w_1,w_2,\cdots w_{i-1}) \approx P(w_1\vert w_{i-N+1},w_{i-N+2},\cdots w_{i-1})\],
上面这种假设被称为n-1阶马尔科夫假设,对应的模型称为N元模型。N=2就是二元模型,N=1其实就是上下文无关的模型,基本不怎么使用。
上面的模型看起来已经很完美了,但是考虑以下两个问题,对于二元模型:
如果此时\(count(w_i,w_{i-1})=0\),是否可以说\(P(w_i\vert w_{i-1})=0\) ?
如果此时\(count(w_i,w_{i-1})=count(w_{i-1})\),是否可以说\(P(w_i\vert w_{i-1})=1\) ?
显然,不能这么武断。
但是,实际上上述两种情况肯定是会出现的,尤其是语料足够大的时候,那么,我们怎么解决上述问题呢?
古德和图灵给出了一个很漂亮的重新估计概率的公式,这个公式后来被称为古德-图灵估计。
古德图灵的原理是:
对于没有看见的事件,我们不能认为他发生的概率就是0,因此从概率的总量中,分配一个很小的比例给这些没有看见的事件。这样一来,看见的那些事件的概率就要小于1了,因此,需要将所有看见的事件的概率调小一点。至于小多少,要根据“越是不可信的统计折扣越多”的方法进行。假定在语料库中出现\(r\)次的词有\(N_r\)个,特别的,未出现的词数量为\(N_0\),语料库大小为\(N\),那么,很显然,
\[N = \sum _{r=1}^ \infty rN_r\],
出现\(r\)次的词在整个语料库中的相对频度则是\({rN_r}/{N}\),如果不做任何处理,这个相对频度作为这些词的概率。但是当\(r\)比较小的时候,统计上可能不可靠,因此需要使用一个更小的次数\(d_r\)来表示,古德-图灵按照如下公式计算\(d_r\):
\[d_r=(r+1)\cdot N_{r+1}/N_r\],
显然
\[\sum_r d_r\cdot N_r = \sum_r (r+1)\cdot N_{r+1} = N\],
此时,
\[d_0 = (0+1)\cdot N_1/N_0 = \frac{N_1}{N_0} > 0\]
在实际处理的时候,一般对出现次数超过某个阈值的词,频率不下调。
基于这种思想,估计二元模型概率的公式如下:
\[P(w_i\vert w_{i-1})= \begin{cases} f(wi\vert w_{i-1}) & {if\quad count(w_{i-1},w_i)} \ge T \f_{gt}(w_i\vert w_{i-1})& if\quad 0 \le count(w_{i-1},w_i) < T \Q(w_{i-1})\cdot f(w_i) & otherwise \end{cases}\],
其中,\(f(\cdot)\)表示相对频度,即频率。
\[Q(w_{i-1})=\frac{1-\sum_{w_i\quad seen}P(w_i \vert w_{i-1})}{\sum _{wi\quad unseen}f(w_i)}\]
上面这种方法称为卡茨退避法。
n-gram模型的作用就是,基于语料库计算出各种词串出现的概率,遇到一个句子的时候,可以直接使用上面所计算的概率,把所有的概率连乘,就得到了整个句子的概率。
机器学习的套路是,对所研究的问题建模,构造一个目标函数,然后优化参数,最后用这个目标函数进行预测。
对于统计语言模型,常使用最大对数似然作为目标函数,即
\[L = \sum_{w\in C}logP(w\vert context(w))\],
在n-gram模型中,\(context(w_i) = (w_{i-n+1},w_{i-n+2},\cdots,w_{i-1})\),
由此可见,概率\(P(w_i\vert context(w_i))\)是关于\(w\)和\(context(w)\)的函数,即
\[P(w\vert context(w)) = F(w,context(w),\theta)\],
一旦\(F\)确定下来了,任何概率都可以使用这个函数进行计算了。
似乎到这里,我们仍然不知道词向量是什么,因为n-gram模型中根本没有用到词向量。那么,接下来将要介绍的神经网络语言模型则是实实在在用到了词向量。之所以提到统计语言模型,是因为它是其他语言模型的基础,我们得知道语言模型是干嘛的,然后再对语言模型进行展开。
上面介绍的n-gram模型相信我们已经十分清楚了,但是n-gram模型的一个突出的确定就是,n的设置不宜过大,n从2到3提升效果显著,但是从3-4提升的效果就没那么好了。而且随着n的增大,参数的数量是以几何形势增长的。
因此,n-gram模型只能提取某个词前面两到三个词的信息,而不能提取更多的信息了。然而很明显的是,整文本序列中,包含更前面的词能够提供比仅仅2到3个词更多的信息,这也是神经网络语言模型着重要解决的问题之一。
神经网络模型主要在以下两点上寻求更大的进步:
n-gram模型没有考虑上下文中更多的词提供的信息
n-gram模型没有考虑词与此之间的相似性。
举个栗子:
如果在一个语料库中,"the cat is walking in the bedroom"出现了5000次,而"a dog is running in the room"只出现了5次,n-gram模型得出的结果是前面一个句子的可能性会比后面一个句子大得多。但是实际上,这两个句子是相似的,他们在真实的情况下出现的概率也应该是相仿的。
神经网络语言模型可以概括为以下三点:
将词汇表中的每个词表示成一个在m维空间里的实数形式的分布式特征向量
使用序列中词语的分布式特征向量来表示连接概率函数
同时学习特征向量和概率函数的参数
特征向量表示词的不同特征:每一个词都是向量空间内的一个点。特征的个数通常都比较小,比如30,60或者100,远远小于词汇表的长度。概率函数是在给定一个词前面的若干词的情况下,该词出现的条件概率。调整概率函数的参数,使得训练集的对数似然达到最大。每个词的特征向量是通过训练得到的,也可以用先验知识进行初始化。
训练集是词序列\(W_1,W_2,...,W_T,W_T\in V\),\(V\)是词汇表,是一个很大但是有限的集合。
目标是找到一个好的模型,使得\(f(W_t,...,W_{t-n+1})=\hat{P}(W_t|W_1^{n-1})\)
唯一的约束条件是\(\sum _{i=1}^{|V|}f(i,W_{t-1},...,W_t-n+1)=1,f>0\)
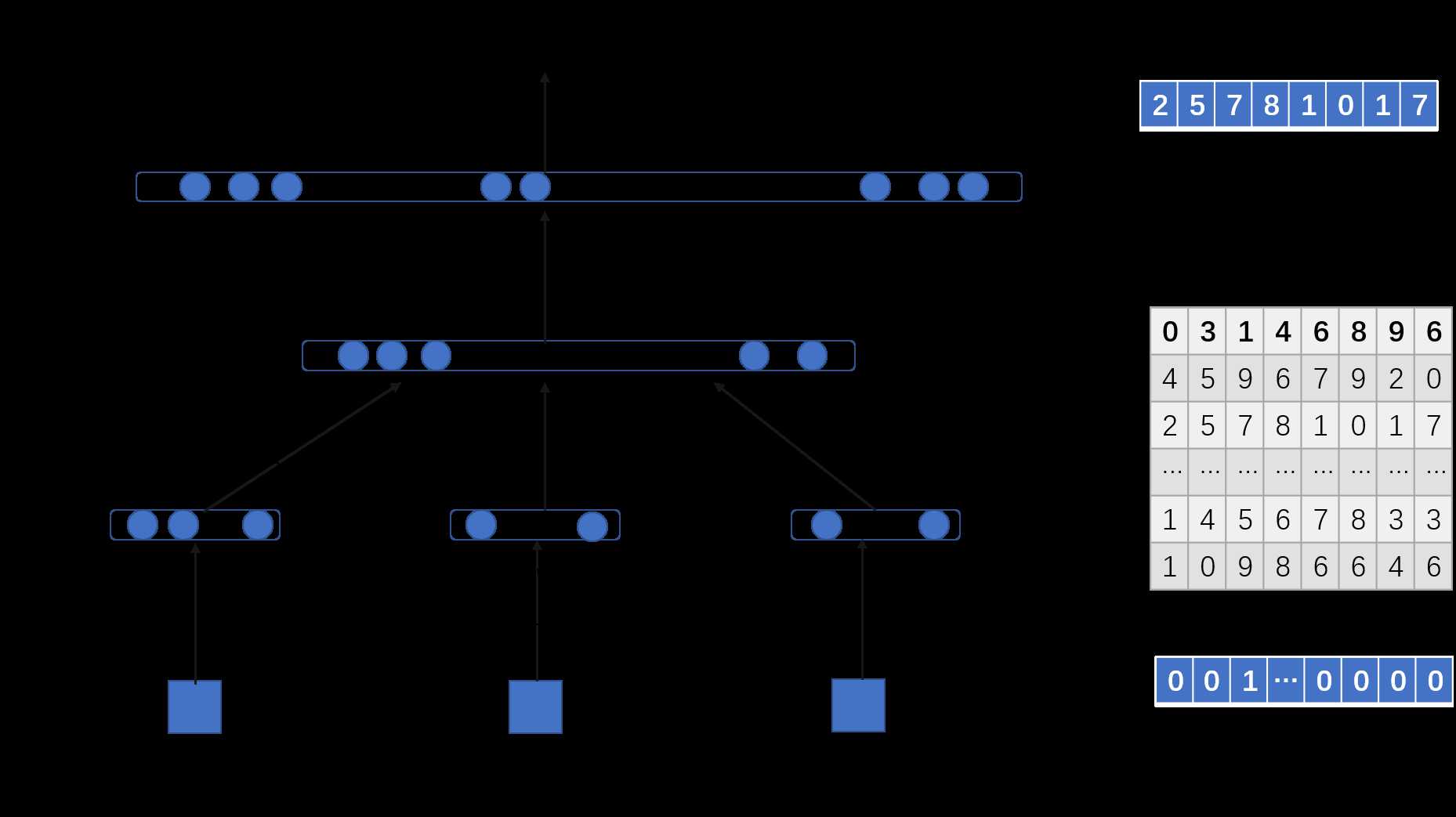
我们将函数\(f(W_t,...,W_{t-n+1})\)分解为以下两个部分:
映射\(C\),将\(V\)中的所有元素映射为真实的向量\(C(i)\in R^m\),\(C(i)\)代表词汇表中的每个词的分布式特征向量,实际上,\(C\)是一个由自由参数构成的\(|V|\times m\)矩阵。其中\(|V|\)代表词汇表的大小,也就是词汇表中的词数量。
每个词的概率函数是由\(C\)来表示的:函数\(g\)将输入的词特征向量\((C(W_{t-n+1}),...,C(W_{t-1}))\)映射为词\(W_t\)前面\(n-1\)个词的条件概率分布。
\[f(i,W_{t-1},...,W_{t-n+1})=g(i,C(W_{t-1}),...,C(W_{t-n+1}))\]
函数\(f\)是由两个映射组成的(\(C\&g\)),\(C\)是所有词共享的。每一个部分都与一些参数有关。
映射\(C\)的参数实际上就是特征向量本身,表示为一个\(|V|\times m\)矩阵,矩阵的每一行代表词\(i\)的特征向量\(C(i)\).
函数\(g\)的参数是\(\omega\),所有的参数就是\(\theta = (C,\omega)\).
当寻找到使得带惩罚项的训练语料库的对数似然率最大的\(\theta\),那么训练完成。
\[L = \frac{1}{T}\sum _t log f(W_t,W_{t-1},...,W_t-n+1)+R(\theta)\]
\(R(\theta)\)是惩罚项,只作用于神经网络的权重和矩阵\(C\)。自由参数的规模是\(V\)的线性函数,也是\(n\)的线性函数。
在下面的大多数试验中,神经网络只有一个隐藏层,外加一个映射层。还有一个可选的直连层。所以说实际上有两个隐藏层,但是由于影射层只是做了一个线性变换,并没有添加新的信息,因此不能视为真正的隐藏层。所以真正的隐藏层就只有一个。
从图中可以看出,最底层实际上就是一些单一的词,表示成one-hot形式,即长度为词汇表的长度。然后,每个one-hot向量分别与投影矩阵C相乘,则原来长度为\(|V|\)的one-hot向量,经过线性变换以后,缩短为一个长度为\(m\)的向量,其中m就是我们设置的特征的个数,一般在2个数量级。投影完成以后,将所有的特征向量按照顺序首尾相连,形成一个长度为\(m(n-1)\)的向量,以词向量作为隐藏层的输入,隐藏层的激活函数为双曲正切函数\(tanh\)。输出层接受隐藏层的输出作为输入,经过一个softmax函数进行转换,得到最终的输出P.
即
\[\hat{P}(w_t\vert w_{t-1},...,w_{t-n+1})=\frac{e^{y_{w_t}}}{\sum_i e^{y_i}}\],
其中
\[y = b+Wx + Utanh(d+Hx)\]
双曲正切函数逐个应用于隐藏层的各个单元。当没有直连的时候,\(W=0\),\(x\)是首尾相连的特征向量:
\[x = (C(w_{t-1}),C(w_{t-2}),...,C(w_{t-n+1}))\]
令\(h\)是隐藏层的单元数,\(m\)是特征向量的长度,当没有直连的时候,\(W=0\)。那么,所有的自由参数就是:
输出层的偏置\(b\),长度为|V|
隐藏层的偏置\(d\),长度为\(h\)
隐藏层到输出层的权重矩阵\(U\),是一个\(|V|\times h\)矩阵
词向量到输出层的权重矩阵\(W\),是一个\(|V|\times (n-1)m\)矩阵
隐藏层权重\(H\),是一个\(h\times (n-1)m\)矩阵
特征矩阵\(C\),是一个\(|V|\times m\)矩阵
此时的输出\(y\)实际上是一个长度为\(|V|\)的向量,那么分量\(y_{wt}\)不能表示给出前(n-1)个词的情况下\(w_t\)的概率,因此需要进行一次归一化。
那么,我们所有的参数如下:
\[\theta = (b,d,W,U,H,C)\]
主要的计算量都集中在隐藏层到输出层的以及输出层的归一化计算。
使用随机梯度下降进行参数求解:
\[\theta \leftarrow \theta + \epsilon\frac{\partial log \hat{P}(w_t\vert w_{t-1},w_{t-2},w_{t-n+1})}{\partial \theta}\]
其中,\(\epsilon\)是学习率。
当训练结束以后,矩阵\(C\)就是我们需要的词向量,每一行代表该位置的词的向量。得到了词向量,就可以进行许多有趣的分析。
比如:
文本聚类
计算文本相似度
其他应用
基本版的skip-gram模型是十分简单的。我们将会训练一个只有一个隐藏层的简单的神经网络来完成我们的任务,但是当神经网络训练完成以后,我们实际上并不使用这个网络做什么,而是获得隐藏层的权重矩阵,这个矩阵实际上就是我们需要的词向量(word vectors)
skip-gram模型需要完成这样的工作:给定一个词,预测其周围的词,或者说在其附近的词。这个神经网络将会计算出我们从词汇表中选出的每个“候选”邻居词的概率。
这里的附近需要说明一下,实际上在算法里有一个"window size"参数,用来控制窗口大小,如果选择参数的值为5,则会预测该词前后各5个词的概率。
skip-gram模型的输入需要经过特殊的调整,不同于上述神经网络语言模型,应该首先将这里的语料整理成词对(word-pair)。
比如对于语句"The quick brown fox jumps over the lazy dog."此处我们选择window size = 2.

具体操作如图所示:
对于单词"The",取其前后两个词与其凑成词对,这里"The"前面没有单词,因此取后面两个,凑成两个词对,分别是(the,quick),(the,brown)。
对于单词quick,其前面有1个单词,后面有2个单词,可以凑成3对,分别为:(quick,the),(quick,brown),(quick,fox)。
对于单词brown,其前面有两个单词,后面有两个单词,可以凑成4对,分别是:(brown,the),(brown,quick),(browm,fox),(brown,fox)。
以此类推,可以把语料库中的所有文本调整成上述词对。
所有的词对都应该是(input,output)形式。
有了词对,接下来看一下skip-gram的最简单的模型长什么样子。
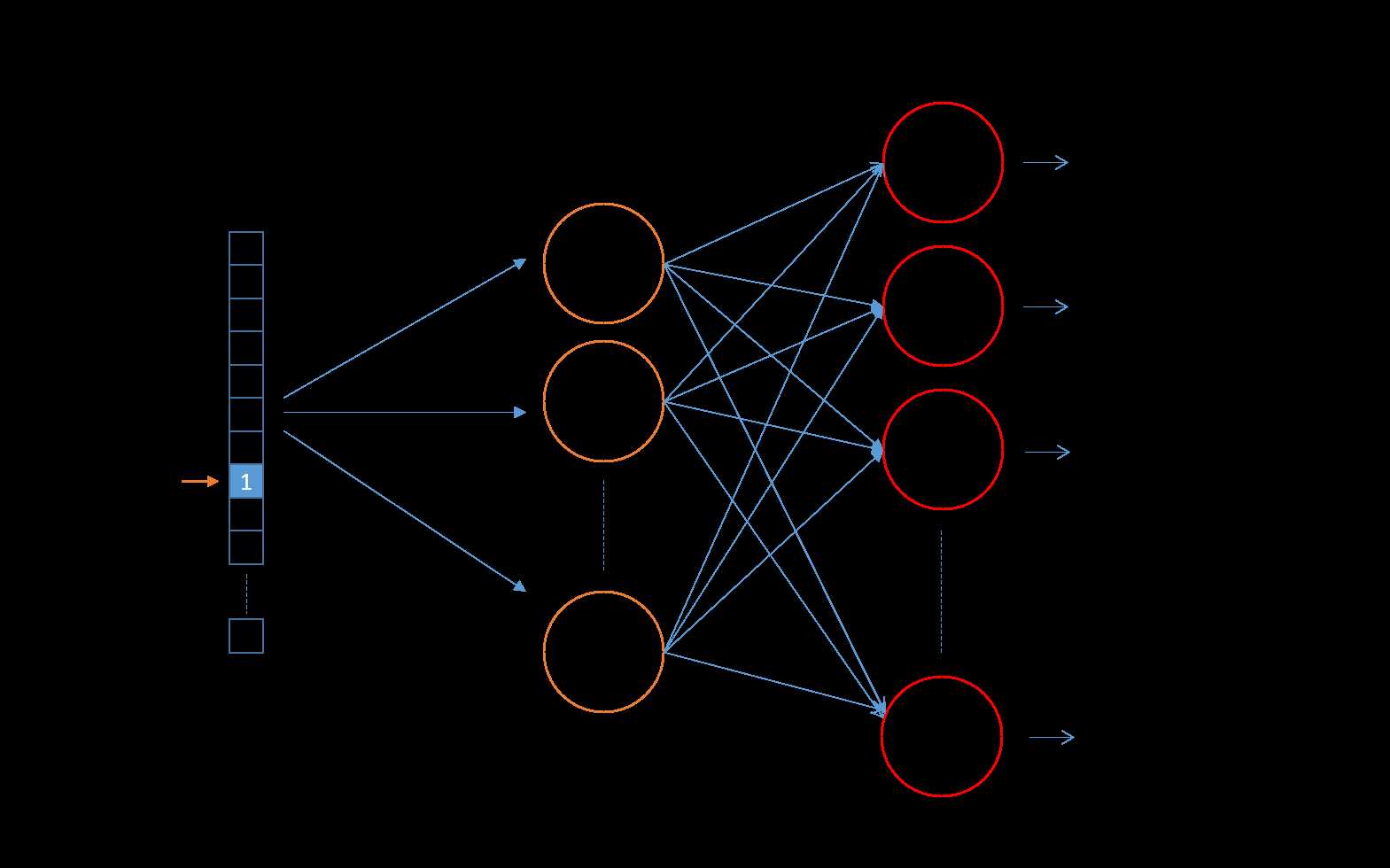
在上图中,可以清晰地看出,skip-gram模型是一个简单的神经网络,有一个隐藏层(实际上在作者的论文中是以投影层的形式表述的),该隐藏层并没有对应的激活函数。
输入数据仍然是one-hot向量,向量只有一个分量是1,其他全为0.向量的长度为词汇表的长度。
对下面所要用的符号进行说明:
\(i\):输入的one-hot向量,长度为|V|
\(|V|\):词汇表的长度
\(P\):输入层到投影层的\(|V|\times m\)权重矩阵
\(W\):投影层到输出层的\(m\times |V|\)权重矩阵
\(y\):输出层输出结果
由于这个神经网络没有激活函数,因此看起来比较简单。
神经网络的计算过程如下:
首先,将输入词向量(one-hot)投影到隐藏层(投影层),即\(i^T\times P=1\times |V|\times |V| \times m=1\times m\)
将隐藏层的结果乘以隐藏层到输出层的权重矩阵\(W\),即\(1\times m \times m\times |V|=1\times |V|\)
将输出层的输出结果进行softmax归一化,即
\[y=\frac{e^{y}}{\sum_{i\in y}e^i }\]
此时\(y\)是一个\(1\times |V|\)向量,向量的每个分量代表给定词\(w_i\)的情况下,其相邻词是词汇表中对应词的概率。将\(y\)与output的one-hot向量相乘,就可以得到给定\(w_i\)的情况下,其相邻词是output的概率,即
\[P(w_o\vert w_i)=y\times w_o\],
其中,\(w_o\)是词output的向量形式。
以上矩阵相乘只是为了说明维度变化,并不是实际上的矩阵乘法。
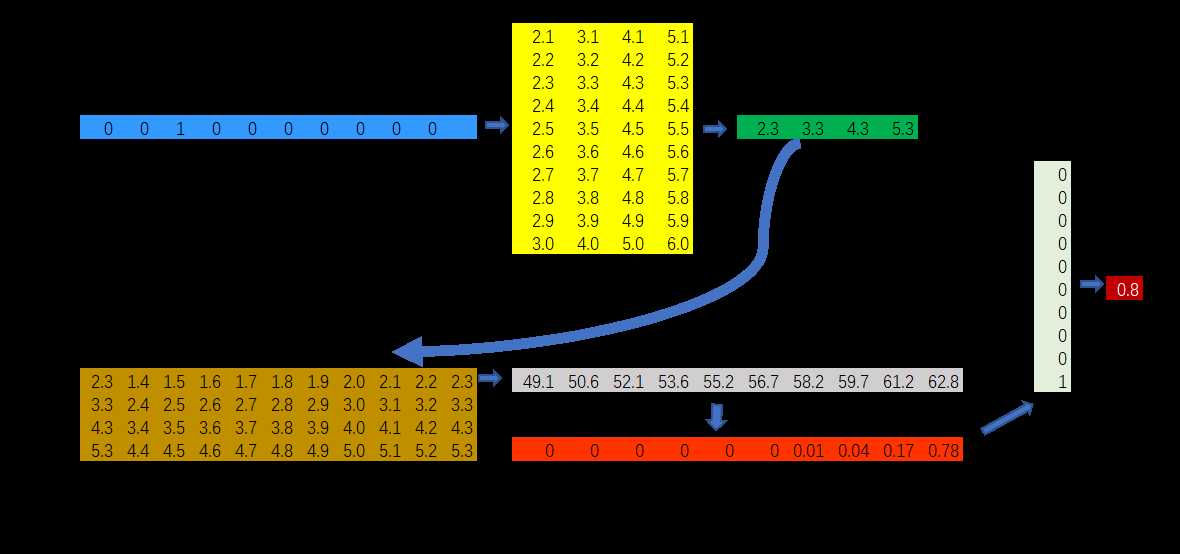
用矩阵说明如下:
假定我们的词库大小为10,输出层到投影层的权重矩阵为\(10\times 4\)矩阵。
我们的输入样本是词对(brown,quick).其中,brown的one-hot表示形式如图中的蓝色向量所示,quick的one-hot表示形式如图中的浅绿色向量所示。
蓝色向量是我们的输入向量,即one-hot向量
黄色矩阵是输入层到投影层的权重矩阵
绿色向量是输入向量与第一个权重矩阵的向量乘积
棕色矩阵是投影层到输出层的权重矩阵
灰色向量是绿色向量与棕色矩阵的矩阵乘积
红色向量是对灰色向量进行了一次\(softmax\)归一化计算
浅绿色矩阵是词对中的输出词对应的one-hot向量
深红色数值是我们计算出的输出词对应的概率
skip-gram的目标是对于训练样本\(w_1,w_2,\cdots,w_T\),最大化如下平均对数似然概率:
\[\frac{1}{T}\sum _{t=1}^T\sum_{-c\le i\le c,j\ne 0}log p(w_{t+j}\vert w_t)\]
实际上,以上模型是难以实现的,因为计算 \(\nabla logp(w_O\vert w_I)\)的代价随着\(W\)的增大而增大(W表示词汇表的长度),经常达到\(10^5-10^7\)数量级。
哈夫曼树是一种最优二叉树,它是这样定义的:
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树。哈夫曼树的构造方法如下:
(1) 将\(w_1,w_2,\cdots,w_n\)看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树
假设我们的权值为:26 24 15 10 17 18 10 27
首先对上面的权值按照从小到大排序:
排序后的权值为:10 10 15 17 18 24 26 27然后。我们按照上述步骤构建哈夫曼树。
此处我们约定将大的权值放在左子树。
---Begin
选择最小的两个权值10,10,合并成一个新树的左右子树。新树的权值为20,删除合并的两个权值,将20加入到森林,此时的权值为(仍然进行排序):15 17 18 20 24 26 27
选择最小的15和17合并,删除15和17,将32加入到森林,此时的权值为:18 20 24 26 27 32
选择最小的18和20合并,删除18和20,将38加入到森林,此时的权值为:24 26 27 32 38
选择最小的24和26合并,删除24和26,将20加入到森林,此时的权值为:27 32 38 50
选择最小的27和32合并,删除27和32,将59加入到森林,此时的权值为:38 50 59
选择最小的38和50合并,删除38和50,将88加入到森林,此时的权值为:59 88
选择最小的59和88合并,删除59和88,将147加入到森林,此时的权值为:147
---End
根据上述权值构造的哈夫曼树如下:
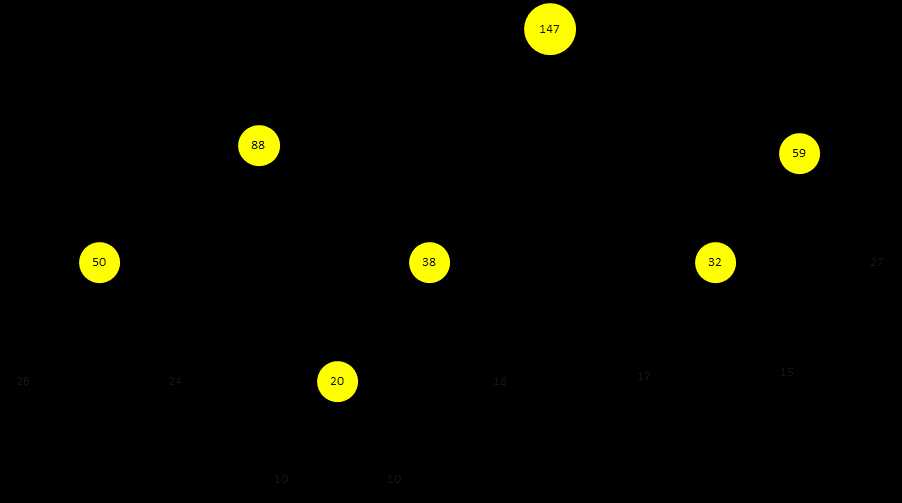
背景为黄色的是新生成的树
逻辑回归通常用来处理二分类问题,因变量通常只有两个可能的取值,自变量既可以是连续型变量,也可以是分类变量。
利用sigmoid函数,对于任意的样本\(x=(x_1,x_2,\cdots,x_n)^T\),可将二分类问题的h函数(hypothesis)写成如下形式:
\[h_\theta(x)=\sigma(\theta_0+\theta_1x_1+\cdots+\theta_nx_n)\],
其中\(\theta =(\theta_0,\theta_1,\cdots,\theta_n)\)为待定参数,为了简化起见,可以引入\(x_0=1\)将\(x\)扩展为\((x_0,x_1,\cdots,x_n)\),于是,\(h_\theta\)可简写为
\[h_\theta(x)=\sigma(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}\]
sigmoid函数图像如下:
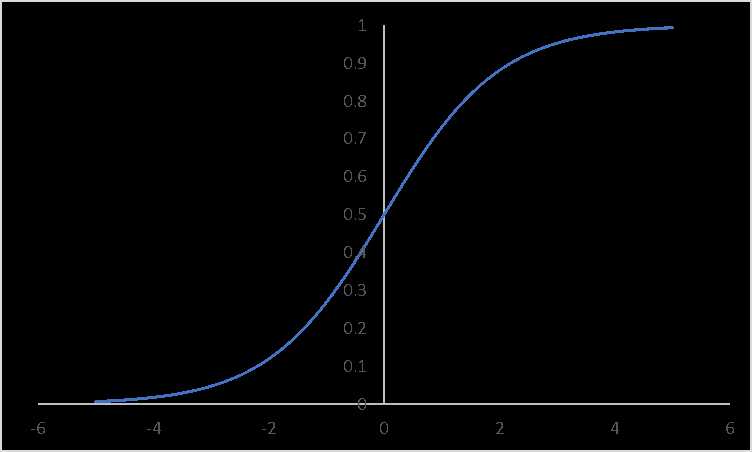
函数\(h_\theta(x)\)的值有特殊的含义,它表示结果取1的概率,因此对于输入\(x\),分类结果为类别1和类别0的概率分别为:
\[P(y=1\vert x;\theta)=h_\theta(x)\]
\[P(y=0\vert x;\theta)=1-h_\theta(x)\]
上式也可以写成如下综合形式:
\[P(y\vert x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}\]
sigmoid函数具有很好的导数特征
已知
\[\sigma(x) = \frac{1}{1+e^{-x}}\]
则
\[\sigma(x)^{'}=\frac{e^{-x}}{(1+e^{-x})^2}=\sigma(x)(1-\sigma(x))\]
另外
\[[log\sigma(x)]^{'}=1-\sigma(x),[log(1-\sigma(x))^{'}=- \sigma(x)\]
hierarchical softmax使用一颗二叉树的叶子结点来代表输出层对应词汇表中每个词的输出结果。每个结点都代表了它的孩子结点的相关概率。这种方式定义了一种给词分配概率的随机游走解决方案。
准确地说,从根结点出发,每一个词都能以一条确定的路径抵达。对所使用的符号作如下阐述:
\(w\):代表词汇表中的词,用叶子结点表示
\(n(w,j)\):从根结点到达某个叶子结点的路径上的第\(j\)个结点,根结点为第一个结点
\(L(w)\):路径的长度,也就是结点的个数
因此,\(n(w,1)=root,n(w,L(w))=w\)
\(n\):非叶子结点
\(ch(n)\):非叶子结点的孩子结点
\([[x]]\):if x is true,than 1,else than -1
hierarchical softmax定义\(P(w_o\vert w_i)\)如下:
\[P(w\vert w_i)=\prod_{j=1}^{L(w)-1}\sigma([[n(w,j+1)=ch(n(w,j))]]\cdot (v^{'}_{n(w,j)})^T v_{w_i})\]
其中
\[\sigma(x)=1/(1+e^{-x})\]
可以证明:
\[\sum _{i=1}^Wp(w\vert w_i)=1\]
那么,hierarchical softmax框架下的skip-gram结构是什么样的呢?
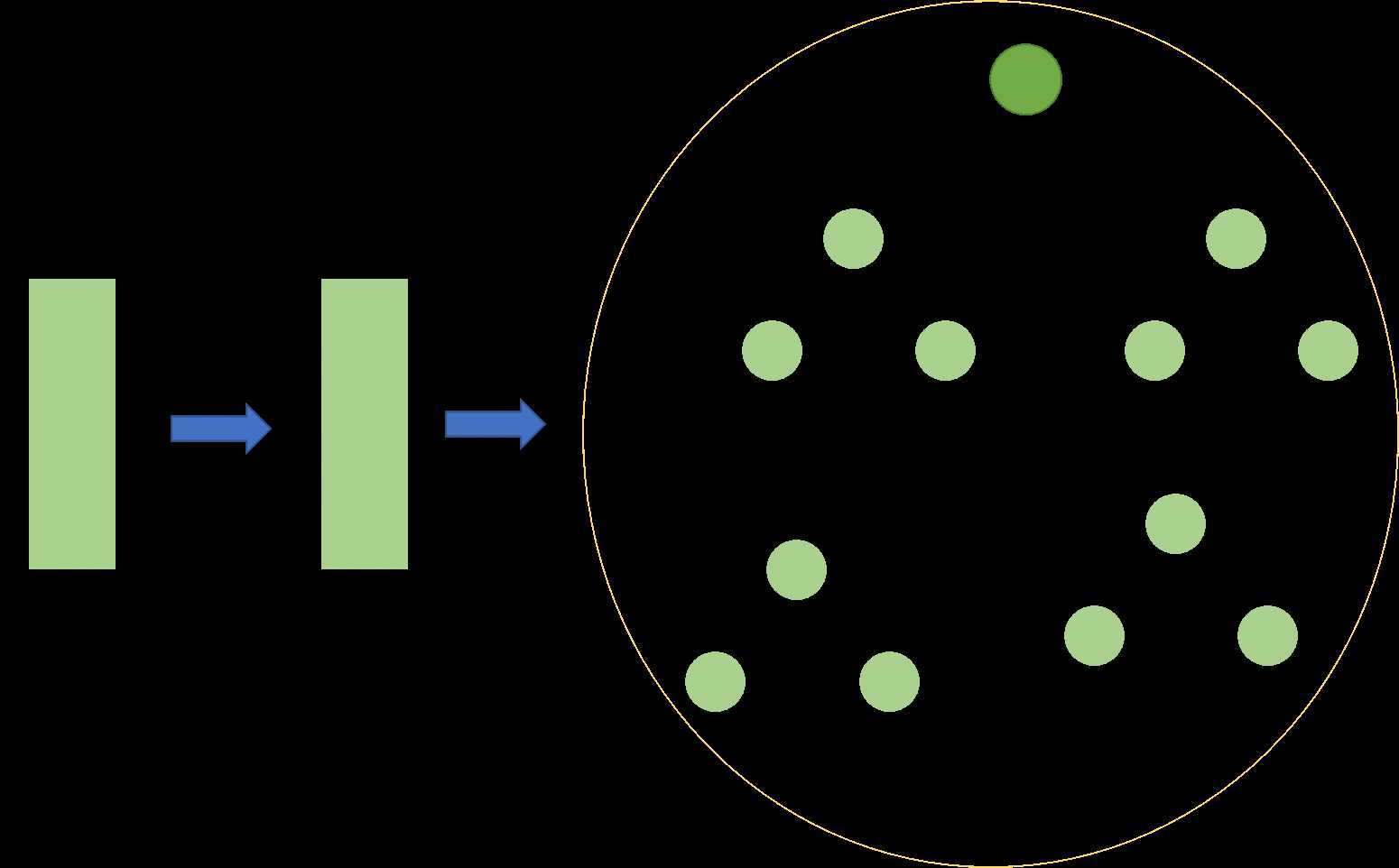
如上图所示,与basic版本的skip-gram模型相比,hierarchical softmax版本的模型输出层不再是线性结构,而是树形结构。
上面已经说过,线性结构的skip-gram模型的参数规模十分庞大,最大能够达到\(10^7\)数量级,再加上动辄10亿级别的语料库,训练代价很高,效率就特别低了。
引入了hierarchical softmax以后,输出层的维度得到了大幅降低。正如作者所说,计算\(logp(w_o\vert w_i)\)和\(\nabla logp(w_o\vert w_i)\)的代价是与\(L(w_o)\)也就是哈夫曼树的深度成正比的。
下面假装正经地推导参数的更新过程:
假设我们的训练样本是【今天我上课迟到了,然后被老师批评了】,对应词汇表中的词汇为【今天 我 上课 迟到 了 然后 被 老师 批评】
假设在语料库中,上述词汇对应的频数如下表所示:
| 词汇 | 频率 |
|---|---|
| 今天 | 8 |
| 我 | 15 |
| 上课 | 2 |
| 迟到 | 1 |
| 了 | 20 |
| 然后 | 10 |
| 被 | 5 |
| 老师 | 3 |
| 批评 | 2 |
将频率看做是哈夫曼树的权值,将大的权值放在左子树,小的权值放在右子树。
绘制出的带权值的哈夫曼树如下:
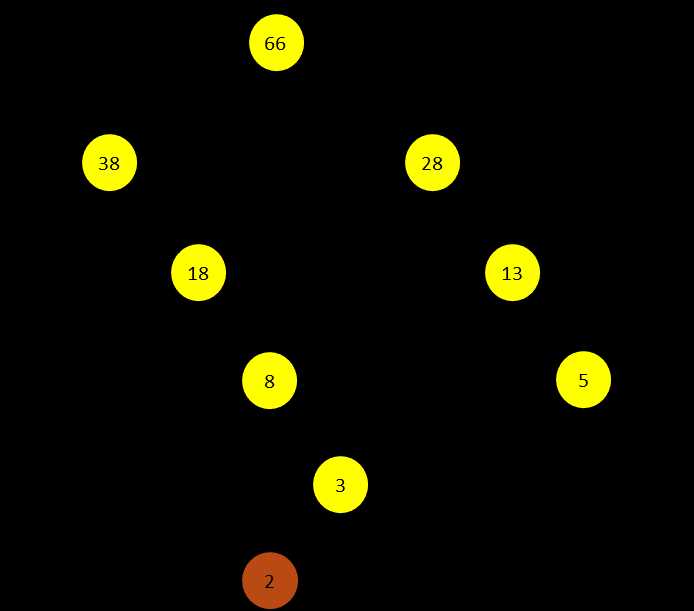
说明如下:
黄色的结点表示新生成的树
\(\theta_i^w \in R^m\),非叶子结点对应的向量
\(d_1^w,d_2^w,\cdots,d_{l(w)-1}^w \in \{0,1\}\):词\(w\)的哈夫曼编码,由\(l(w)-1\)位编码构成,\(d_j^w\)对应对应路径中第\(j\)个非叶子结点的编码(0 or 1).
根据基于hierarchical softmax的skip-gram模型,投影层将输入的one-hot向量投影成\(R^m\)空间中的向量,即输出层接受的输入为投影层的输出,即\(v_m\)。
目标函数仍然是最大化对数似然概率,那么,当前的重点是条件概率函数的构造。
skip-gram模型将其定义为
\[P(context(w_i)\vert w_i)=\prod _{u\in context(w_i)}p(u\vert w_i)\]
而根据hierarchical softmax的思想,\(p(u\vert w_i)\)可以写出如下形式:
\[p(u\vert w_i)=\prod _{j=2}^{l(w)}p(d_j^u\vert v_m;\theta_{j-1}^u)\]
其中
\[p(d_j^u\vert v_m;\theta_{j-1}^u)=[\sigma(v_m^T\theta^u_{j-1})]^{1-d_j^u}\cdot[1-\sigma(v_m^T\theta^u_{j-1})]^{d_j^u}\]
那么,我们的目标函数可以写成如下形式:
\[L=\sum _{w\in C} log \prod _{u\in context(w)}\prod _{j=2}^{l(w)}[\sigma(v_m^T\theta^u_{j-1})]^{1-d_j^u}\cdot[1-\sigma(v_m^T\theta^u_{j-1})]^{d_j^u}\]
\[=\sum _{w\in C}\sum _{u \in context(w)}\sum _{j=2}^{l(w)}\{(1-d_j^u)\cdot log[\sigma(v_m^T\theta^u_{j-1})]+d_j^u\cdot log[1-\sigma(v_m^T\theta^u_{j-1})]\}\]
上面的函数就是skip-gram的目标函数,为了方便推导梯度,将三重求和符号下花括号的内容简记为\(L(w,u,j)\),即
\[L(w,u,j)=(1-d_j^u)\cdot log[\sigma(v_m^T\theta^u_{j-1})]+d_j^u\cdot log[1-\sigma(v_m^T\theta^u_{j-1})]\]
首先考虑\(L\)关于\(\theta_{j-1}^u\)的梯度计算:
\[\frac{\partial L}{\partial \theta_{j-1}^u}=\frac{\partial L(w,u,j)}{\partial \theta_{j-1}^u}=\frac{\partial \{(1-d_j^u)\cdot log[\sigma(v_m^T\theta^u_{j-1})]+d_j^u\cdot log[1-\sigma(v_m^T\theta^u_{j-1})]\}} {\partial \theta_{j-1}^u}=[1-d_j^u-\sigma(v_m^T\theta_{j-1}^u)]\cdot v_m\]
于是,\(\theta_{j-1}^u\)的更新公式可写为:
\[\theta_{j-1}^u\leftarrow \theta_{j-1}^u+\epsilon [1-d_j^u-\sigma(v_m^T\theta_{j-1}^u)]\cdot v_m\]
接下来考虑\(L\)对\(v_m\)的梯度。由于在\(L\)中,\(v_m\)与\(\theta_{j-1}^u\)具有对称性,因此可以根据上述所求,直接写出\(v_m\)的更新公式:
\[v_m\leftarrow v_m+\epsilon \sum _{u\in C}\sum _{j=2}^{l(w)}\frac{\partial L(w,u,j)}{\partial v_m}\]
其中,\(\epsilon\)是学习率。
考虑到basic版本的skip-gram模型拥有两个异常巨大的权重矩阵,再加上一个10亿数量级的语料库,神经网络跑起来会非常吃力。
word2vec的作者是这样处理这个问题的,主要有以下三个创新点:
将常用词对或者词组看成一个单独的词
subsampling(降采样)出现频率很高的词以减小训练样本的大小
使用一种被称为"Negative Sampling"的方法来改变优化目标,这种方法在训练时只优化与训练样本有关的很小一丢丢权重。
值的一提的是,应用Subsampling和NEG方法不仅可以减小计算压力,还能提高最终产生的词向量的质量。
回想一下那个basic版本的skip-gram,神经网络的真实值或者说标签是一个one-hot矩阵,也就是说,只有一个分量是1,而其他分量都是0(成千上万个0)。但是我们在更新神经网络权重的时候,对于所有的输出为0的权重都进行了更新,这样效率是比较差的。
negative sampling的思想就是,当我们在训练一个特定样本的时候,能不能只更新几个输出为0的权重,这样计算起来就比较轻松了。
我们把one-hot向量分量为负的位置所对应的词称为negative words,在训练一次样本时,我们只更新几个(假如说5个吧)negative words,同时也更新我们的pisitive words(即分量为1所对应的位置在词汇表中对应的词)。
作者在论文中说到,当样本量比较小的时候,选择5-20个negative words效果会比较好,当样本量比较大的时候,2-5个negative words就能得到很好的效果。
现在假设我们在basic model中需要更新的权重矩阵为\(300\times 10000\)矩阵,那么basic model每次迭代需要更新\(3\times 10^6\)个参数,而采用了negative sampling 方法以后,我们只需要更新5个negative words和1个positive words对应的权重,也就是\(300\times (5+1)=1800\)个权重,是原来的\(1800/3\times 10^6=0.06\%\).
想法是好的,我们要怎么选择这5个negative words呢?
我们知道,语料库中的每个词都有一定的频率,那么我们就利用频率这个信息,对negative words进行采样。
由此可见,高频词被选为negative words的概率就比较大,同理,低频词被选为negative words的概率就比较小。
作者的处理方法是,赋予每一个词被选为negative words的概率,具体计算公式如下:
\[P(w_i)=\frac{f(w_i)^{0.75}}{\sum _{j=0}^nf(w_i)^{0.75}}\],
至于为什么是0.75,这是作者及其团队经过不断试验得出的效果比较好的,没有特别的原因。
计算出了概率,我们又怎么选择相应的negative words呢?
作者在其代码中给出了答案。
下面给出了具体的方法:
构造一个很长的数组,作者的数组长度达到了1000000
将词汇表中的每个词对应的index(索引)向数组中填充多次,填充的次数是这样计算的:
根据一元模型可以从语料库生成样本(也就是把语料库中的文本以词的形式展示)
填充次数times的计算公式为:
\[times = P(w_i)\times 100000\]
不难理解,\(P(w_i)\)大的被选中的概率就大。
让我们再看一遍词对的生成过程。

如上图所示,我们设定window size = 2 来生成样本。对于包含"the"的词对来说,有以下两个问题:
当我们在寻找词对的时候,("fox","the")所能提供的信息并不比"fox"多。然而,"the"几乎在上面的所有词对中都有出现。
形如("the",...)这样的词对已经远远超过了我们的需求。
word2vec 应用了一种称之为subsampling的方法来解决这个问题。
对于我们遇到每一个语料库中的词,都有一定的概率将它从语料库中删除,删除的概率与该词出现的频率有关。
如果我们将window size 设置为10,我们是这样删除"the"相关样本的:
我们在训练其他词的时候,"the"不会出现在他们的窗口
当输入词是"the"的时候,将样本数减少10个(不减少的情况下是20)
那么,我们怎么决定是否删除一个词呢?
假设\(w_i\)是待定删除的词,\(z(w_i)\)是\(w_i\)在语料库中出现的频率,\(P(w_i)\)是保留该词的概率:
\[P(w_i)=(\sqrt{\frac{z(w_i)}{0.001}}+1)\cdot \frac{0.001}{z(w_i)}\]
0.001也是一个经验参数,如果比0.001还要小,那么保留词的概率就会更小。
下面是\(P(w_i)\)函数的图像:
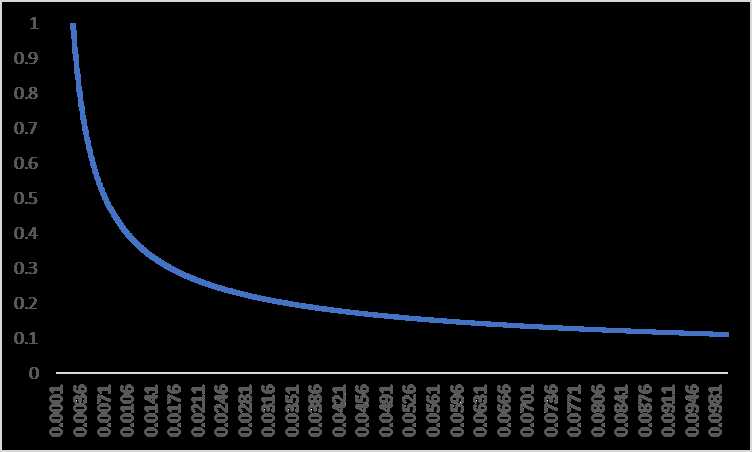
从图像可以看出:
当频率等于0.0026的时候,被保留的概率为1,也就是说,当频率大于0.0026的时候,就有可能被删除。
当频率为0.0074的时候,有一半的概率会被保留
当频率为0.1的时候,被保留的概率就骤减到0.1
learning phrase 方法使得样本更加接近真实世界。考虑以下句子:
New York is a beautiful and modern city where I want to have a travel.我们设置窗口大小为4,对beautiful进行采样,获得如下样本:
(beautiful,New) (beautiful,York) (beautiful,is) (beautiful,a) (beautiful,New) (beautiful,and) (beautiful,modern) (beautiful,city) 采用一元的方法,会将常用的词组分开,从而降低词向量的质量。
我们可以采取一个简单的数据驱动的方法,来对两个词是否能组成词组进行打分:
\[score(w_i,w_j) = \frac{count(w_iw_j)-\delta}{count(w_i)\times count(w_j)}\]
\(\delta\)作为一个折扣系数的作用,用来防止那些不怎么经常一起出现的词语形成词组。当score超过了我们设置的阈值时,将两个词视为词组。
上述打分程序可以多进行几次,以获得三元组或者更多词的词组。
[1]McCormick, C. (2016, April 19). Word2Vec Tutorial - The Skip-Gram Model. Retrieved from http://www.mccormickml.com
[2]Pennington J, Socher R, Manning C. Glove: Global Vectors for Word Representation[C]// Conference on Empirical Methods in Natural Language Processing. 2014:1532-1543.
[3]Mikolov T, Le Q V, Sutskever I. Exploiting Similarities among Languages for Machine Translation[J]. Computer Science, 2013.
[4]Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
[5]Bengio, Y & Ducharme, Réjean & Vincent, Pascal. (2000). A Neural Probabilistic Language Model. Journal of Machine Learning Research. 3. 932-938. 10.1162/153244303322533223.
[6]NSS,(JUNE 4, 2017).An Intuitive Understanding of Word Embeddings: From Count Vectors to Word2Vec.Retrieved from https://www.analyticsvidhya.com/blog/2017/06/word-embeddings-count-word2veec/
[7]peghoty,2014年07月.word2vec 中的数学原理详解.http://blog.csdn.net/itplus/article/details/37969519
[8]吴军.数学之美[M].北京:人民邮电出版社,2014.
==========================The End=============================
标签:code math nal max 聚类 image https 结构 matrix
原文地址:http://www.cnblogs.com/f-young/p/7906451.html