单源最短路径（dijkstra算法）php实现

标签：php   算法   dijkstra   

2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+cost[i][j]})

3.知道U=V，停止。

利用php特有的性质，其代码如下：

function dijkstra(){		
	$node_info_arr=array(	//结点的邻接表结构
		array(
			‘node_id‘=>0,		//某个结点的id
			‘next_node‘=>array(4,2,1),
			‘node_type‘=>0,
			‘cost‘=>array(10,30,100)
			),
		array(
			‘node_id‘=>4,		//某个结点的id
			‘next_node‘=>array(3),
			‘node_type‘=>1,
			‘cost‘=>array(50)
			),
		array(
			‘node_id‘=>3,		//某个结点的id
			‘next_node‘=>array(1),
			‘node_type‘=>1,
			‘cost‘=>array(10)
			),
		array(
			‘node_id‘=>2,		//某个结点的id
			‘next_node‘=>array(3,1),
			‘node_type‘=>1,
			‘cost‘=>array(60,60)
			),
		array(
			‘node_id‘=>1,		//某个结点的id
			‘next_node‘=>array(),
			‘node_type‘=>2,
			‘cost‘=>array()
			)
	);
	
	$start_node_id=false;		//起始结点id
	$i_cost=array(array());	//两个节点之间的开销
	$i_dist=array();		//起始点到各点的最短距离
	$b_mark=array();		//是否加入了
	foreach($node_info_arr as &$node_info){
		if($node_info[‘node_type‘]==0){
			$start_node_id=$node_info[‘node_id‘];			//找到初始节点
		}
		foreach($node_info[‘next_node‘] as $key=>$next_node){
			$i_cost[$node_info[‘node_id‘]][$next_node]=$node_info[‘cost‘][$key];
		}
		$i_dist[$node_info[‘node_id‘]]=‘INF‘;				//初始化为无穷大
		$b_mark[$node_info[‘node_id‘]]=false;				//初始化未加入
	}
	if($start_node_id===false){
		return ‘302‘;
	}
	//计算初始结点到各节点的最短路径
	$i_dist[$start_node_id]=0;	//初始点到其本身的距离为0
	$b_mark[$start_node_id]=true;	//初始点加入集合
	
	$current_node_id=$start_node_id;	//最近加入的节点id
	$node_count=count($node_info_arr);
	for($i=0;$i<$node_count;$i++){
		$min=‘INF‘;								//当前节点的最近距离
		if(is_array($i_cost[$current_node_id])){
			foreach($i_cost[$current_node_id] as $key=>$val){
				if($i_dist[$key]==‘INF‘||$i_dist[$key]>$i_dist[$current_node_id]+$val){
					$i_dist[$key]=$i_dist[$current_node_id]+$val;
				}
			}
		}
		foreach($i_dist as $key=>$val){
			if(!$b_mark[$key]){
				if($val!=‘INF‘&&($min==‘INF‘||$min>$val)){
					$min=$val;
					$candidate_node_id=$key;	//候选最近结点id
				}
			}
		}
		if($min==‘INF‘){
			break;
		}
		$current_node_id=$candidate_node_id;
		$b_mark[$current_node_id]=true;
	}
	foreach($i_dist as $key=>$val){
		echo $start_node_id.‘=>‘.$key.‘:‘.$val.‘<br />‘;
	}
}

 其中例子为图：
    
运行结果为：
    0=>0:0
    0=>4:10
    0=>3:60
    0=>2:30
    0=>1:70

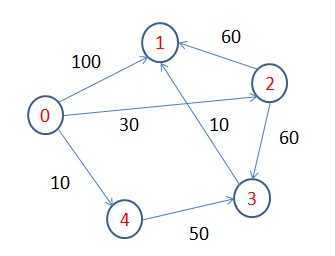
单源最短路径（dijkstra算法）php实现,布布扣,bubuko.com

单源最短路径（dijkstra算法）php实现

标签：php   算法   dijkstra   

原文地址：http://blog.csdn.net/kangrydotnet/article/details/25471709