标签:函数极值 for 解释 0.00 基本 es2017 details key 输出
关于粒子群优化算法(PSO)的解释:http://blog.csdn.net/myarrow/article/details/51507671 (等网上各种参考资料)
用PSO找函数极值。
function [ f ] = fun( x, y ) %UNTITLED2 此处显示有关此函数的摘要 % 此处显示详细说明 a = 50; b = 50; f = (x-a)^2 + (y-b)^2; end
构造了一个二元函数,很明显,有极小值,在(50, 50)。
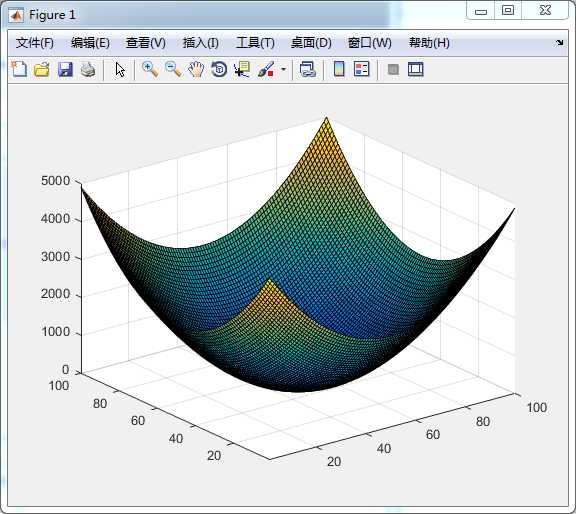
用五个粒子去找。每个点对应的函数输出值即视为粒子的适应度。
1 clear all; 2 clc; 3 % initialize 4 n = 5; 5 P = rand(5, 2) * 100; 6 p = cell(5, 1); 7 for i = 1: n 8 p(i, 1) = {[P(i, 1), P(i, 2)]}; 9 end 10 v = rand(5, 2) * 0.5; 11 vmax = 0.5; 12 pbest = p; 13 gbest = cell(1); 14 fit_v = zeros(5, 1); 15 key = 1; 16 for i = 1: n 17 fit_v(i, 1) = fun(p{i}(1), p{i}(2)); 18 if( fit_v(i, 1) < fit_v(key, 1) ) 19 key = i; 20 end 21 end 22 gbest(1) = pbest(key, 1); 23 % loop 24 t = 1; 25 while(t < 300) 26 for i = 1: n 27 for j = 1: 2 28 v(i, j) = v(i, j) + 2*rand()*(pbest{i, t}(j)-p{i}(j)) + 2*rand()*(gbest{t}(j)-p{i}(j)); 29 if( abs(v(i, j)) > vmax ) 30 v(i, j) = abs(v(i, j)) / v(i, j) * vmax; 31 end 32 p{i}(j) = p{i}(j) + v(i, j); 33 end 34 fit_v_temp = fun(p{i}(1), p{i}(2)); 35 if( fit_v_temp < fit_v(i, t) ) 36 fit_v(i, t+1) = fit_v_temp; 37 pbest(i, t+1) = p(i); 38 else 39 fit_v(i, t+1) = fit_v(i, t); 40 pbest(i, t+1) = pbest(i, t); 41 end 42 end 43 t = t + 1; 44 key = 1; 45 for i = 1: n 46 if( fit_v(i, t) < fit_v(key, t) ) 47 key = i; 48 end 49 end 50 gbest(t) = pbest(key, t); 51 end
运行结果:[50.0030796073836,50.0004541255463]
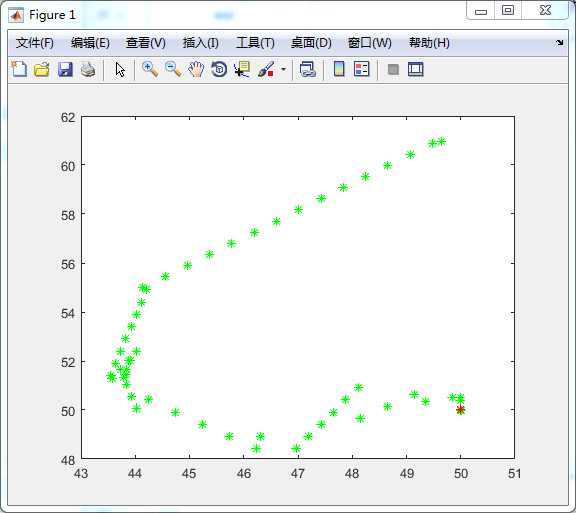
图1 gbest轨迹(红点表示最后收敛位置)
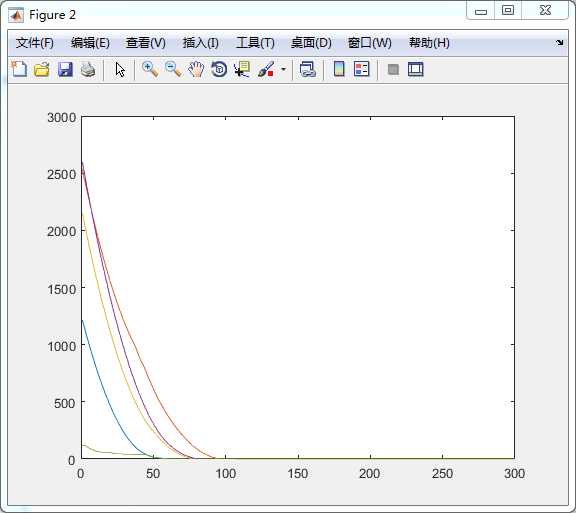
图2 各个粒子的适应度曲线
可以发现在100次左右就基本收敛了。
标签:函数极值 for 解释 0.00 基本 es2017 details key 输出
原文地址:http://www.cnblogs.com/Zzz-y/p/7978090.html