标签:就是 scan 差分 cto 主席树 efi 它的 数组 时间复杂度
题目意思非常清楚,就是要求树上带修改的路径k大值
如果不带修改的话,我会用树上主席树去搞,以父子关系建树,可以参见 [BZOJ 3123]森林
但是带修改就不会打了QAQ,于是去学了另一种在dfs序上搞的方法(同时感谢呵呵酵母菌的帮助)
其实思想是一样的,就是搞出来节点到根路径的线段树,然后用x+y-lca-fa(lca)去差分出来树上路径的线段树,再去里面查询k值
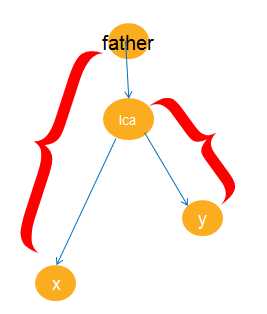
那么我们怎么得到点到根路径的线段树呢?可以在dfs序上差分啊!
dfs序列上的dfnl[x]~dfnr[x]包含的是以x为根节点的子树的dfs序(这个学过dfs序的应该都知道)
对于一个节点x,它的值只会对于它的子树内的点造成贡献,于是我们在dfs序上dfnl[x]的位置+1,dfnr[x]+1的位置-1,这样我们求前缀和的时候就会把这个子树内的值给差分掉
意思就是说,求x到root的路径线段树,我们求dfnl[x]的前缀和线段树就好了,因为这个路径之外的子树或节点,要么在dfnl[x]的后边,要么就被前缀和差分掉了
因为带修改,所以用树状数组维护。然后我就没有打主席树,而是打树状数组套动态开点线段树(相当于直接把线段树类比数组来用了)
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define pos(i,a,b) for(int i=(a);i<=(b);i++)
#define N 101000
#define lc(x) (tree[x].lc)
#define rc(x) (tree[x].rc)
#include<vector>
using namespace std;
vector<int> b;
int lowbit(int x){return x&(-x);}
int findx(int x){
return lower_bound(b.begin(),b.end(),x)-b.begin()+1;
}
int n,q,a[N],root[N],size,len;
int p[N][20],dep[N],fa[N];
struct haha{
int lc,rc,sum;
}tree[N*100];
struct xixi{
int next,to;
}edge[N*2];
int head[N],cnt=1;
void add2(int u,int v){
edge[cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt++;
}
int dfnl[N],dfnr[N],ji;
void dfs(int x){
dfnl[x]=++ji;
for(int i=head[x];i;i=edge[i].next){
int to=edge[i].to;
if(to!=fa[x]){
fa[to]=x;
dep[to]=dep[x]+1;
dfs(to);
}
}
dfnr[x]=ji;
}
void init(){
for(int j=0;(1<<j)<=n;j++) pos(i,1,n) p[i][j]=-1;
pos(i,1,n) p[i][0]=fa[i];
for(int j=1;(1<<j)<=n;j++){
pos(i,1,n){
if(p[i][j-1]!=-1){
p[i][j]=p[p[i][j-1]][j-1];
}
}
}
}
int lca(int a,int b){
if(dep[a]<dep[b]) swap(a,b);
int i;for(i=0;(1<<i)<=dep[a];i++);i--;
for(int j=i;j>=0;j--){
if(dep[a]-(1<<j)>=dep[b]) a=p[a][j];
}
if(a==b) return a;
for(int j=i;j>=0;j--){
if(p[a][j]!=p[b][j]&&p[a][j]!=-1){
a=p[a][j];b=p[b][j];
}
}
return fa[a];
}
struct nono{
int k,a,b;
}ques[N];
void update(int &rt,int l,int r,int pos,int num){
if(!rt) rt=++size;
tree[rt].sum+=num;
if(l==r) return;
int mid=(l+r)>>1;
if(pos<=mid) update(lc(rt),l,mid,pos,num);
else update(rc(rt),mid+1,r,pos,num);
tree[rt].sum=tree[lc(rt)].sum+tree[rc(rt)].sum;
}
void add(int x,int pos,int num){
while(x<=n){
update(root[x],1,len,pos,num);
x+=lowbit(x);
}
}
int cunx[200],cuny[200],cunlca[200],cunfalca[200];
int query(int l,int r,int k){
if(l==r) return l;
int sumx(0),sumy(0),sumlca(0),sumfalca(0);
pos(i,1,cunx[0]){
sumx+=tree[lc(cunx[i])].sum;
}
pos(i,1,cuny[0]){
sumy+=tree[lc(cuny[i])].sum;
}
pos(i,1,cunlca[0]){
sumlca+=tree[lc(cunlca[i])].sum;
}
pos(i,1,cunfalca[0]){
sumfalca+=tree[lc(cunfalca[i])].sum;
}
int mid=(l+r)>>1;
int temp=sumx+sumy-sumlca-sumfalca;
if(temp>=k){
pos(i,1,cunx[0]){
cunx[i]=lc(cunx[i]);
}
pos(i,1,cuny[0]){
cuny[i]=lc(cuny[i]);
}
pos(i,1,cunlca[0]){
cunlca[i]=lc(cunlca[i]);
}
pos(i,1,cunfalca[0]){
cunfalca[i]=lc(cunfalca[i]);
}
return query(l,mid,k);
}
else{
pos(i,1,cunx[0]){
cunx[i]=rc(cunx[i]);
}
pos(i,1,cuny[0]){
cuny[i]=rc(cuny[i]);
}
pos(i,1,cunlca[0]){
cunlca[i]=rc(cunlca[i]);
}
pos(i,1,cunfalca[0]){
cunfalca[i]=rc(cunfalca[i]);
}
return query(mid+1,r,k-temp);
}
}
int la;
int Query(int x,int y,int k){
int falc=fa[la];
cunx[0]=cuny[0]=cunlca[0]=cunfalca[0]=0;
int tx=dfnl[x],ty=dfnl[y],tlca=dfnl[la],tfalc=dfnl[falc];
while(tx>0){
cunx[++cunx[0]]=root[tx];
tx-=lowbit(tx);
}
while(ty>0){
cuny[++cuny[0]]=root[ty];
ty-=lowbit(ty);
}
while(tlca>0){
cunlca[++cunlca[0]]=root[tlca];
tlca-=lowbit(tlca);
}
while(tfalc>0){
cunfalca[++cunfalca[0]]=root[tfalc];
tfalc-=lowbit(tfalc);
}
return query(1,len,k);
}
int main(){
scanf("%d%d",&n,&q);len=n+q;
pos(i,1,n) scanf("%d",&a[i]),b.push_back(a[i]);
pos(i,1,n-1){
int x,y;scanf("%d%d",&x,&y);
add2(x,y);add2(y,x);
}
pos(i,1,q){
scanf("%d%d%d",&ques[i].k,&ques[i].a,&ques[i].b);
if(ques[i].k==0){
b.push_back(ques[i].b);
}
}
sort(b.begin(),b.end());
b.erase(unique(b.begin(),b.end()),b.end());
dfs(1);
init();
pos(i,1,n){
add(dfnl[i],findx(a[i]),1);
add(dfnr[i]+1,findx(a[i]),-1);
}
pos(i,1,q){
int k=ques[i].k,x=ques[i].a,y=ques[i].b;
if(!k){
add(dfnl[x],findx(a[x]),-1);
add(dfnr[x]+1,findx(a[x]),1);
add(dfnl[x],findx(y),1);
add(dfnr[x]+1,findx(y),-1);
a[x]=y;
}
else{
la=lca(x,y);
int jishu=dep[x]+dep[y]-2*dep[la]+1;
if(jishu<k) printf("invalid request!\n");
else printf("%d\n",b[Query(x,y,jishu-k+1)-1]);
}
}
return 0;
}
感悟:
这道题为我提供了一个新的思路,就是可以把树上的东西搞到dfs序上(原来也一直知道但是从来没打过T-T),因为在序列上可以用高级数据结构搞事
在dfs序上差分,求出节点到root想要的答案,然后再在树上差分。妙啊!
比如说最简单的,求带修改树上路径长度,我们可以用这种方法代替树链剖分(时间复杂度理论分析O(nlogn),似乎要快啊OvO)
嗯。学习到了。
[BZOJ 1146]网络管理Network 树上带修改路径k值
标签:就是 scan 差分 cto 主席树 efi 它的 数组 时间复杂度
原文地址:http://www.cnblogs.com/Hallmeow/p/8000316.html