标签:adk 返回 rgs ati 构造 处理 增加 str 查询
树状数组(Binary Indexed Tree(BIT),Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于快速查询任意两位之间的所有元素之和,是一种很实用的数据结构。它通过用节点i,记录数组下标在[ i –2^k + 1, i ]这段区间的所有数的信息(其中,k为i的二进制表示中末尾0的个数,设lowbit(i) = 2^k),实现在O(log n) 时间内对数组数据的查找和更新。
例一:
一个学校有n个班级,起初每个班级都没有学生,学校的招生办遇到了一个棘手的问题,他们必须随时了解前n个班级的总人数(任务一),并且随时会增加若干人到某一个班级(任务二)。我们可以很容易的想到一个简单的算法,开一个长度为n的一位数组记录每个班的人数,这样完成任务二的时间复杂度是 O(1),但是完成任务一的时间复杂度是O(n)所以速度较慢。
我们也可以用A[i]记录前i个班级的总人数,这样完成任务一的时间复杂度是O(1)但是完成任务二的时间复杂度是O(n)。以上两种方法在n很大的情况下速度都比较慢。所以我们必须引入新的数据结构——数状数组。
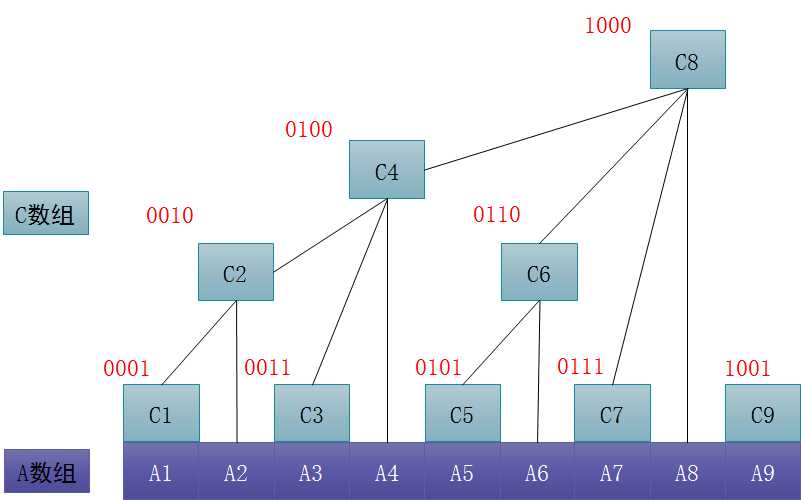
我们同样以例一为例,定义数组A,其中A[i]表示第i个班级的人数。再定义一个数组C[i]其中C[i]=A[i-2^k+1]+……+A[i](k为i在二进制形式下末尾0的个数)。由C数组的定义可以得出
C[1]=A[1]
C[2]=A[1]+A[2]=C[1]+A[2]
C[3]=A[3]
C[4]=A[1]+A[2]+A[3]+A[4]=C[2]+C[3]+A[4]
C[5]=A[5]
C[6]=A[5]+A[6]=C[5]+A[6]
C[7]=A[7]
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]=C[4]+C[6]+C[7]+A[8]
………………
直观地表示如下图:
1. 数组生成
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数,即2^k表示x的二进制最后一位1代表的数)个元素。因为这个区间最后一个元素必然为A[x],所以很明显:C[n] = A[n – 2^k + 1] + ... + A[n],算这个2^k的值有一个快捷的办法,定义一个函数如下即可:
利用机器补码特性:
int lowbit(int x)
{
return x&(-x);
}
例:计算C[6]
6的二进制表示为0110
-6的二进制表示为1010(6的补码)
则 0110
& 1010
0010 = 2
表示C[6]节点管理的区间为2
C[6] = A[5] + A[6]
2. 查询
当想要查询一个sum(n)(求A[n]的和),可以依据如下算法即可:
step1: 令sum = 0,转第二步;
step2: 假如n <= 0,算法结束,返回sum值,否则sum = sum + C[n],转第三步;
step3: 令n = n – lowbit(n),转第二步。
可以看出,这个算法就是将这一个个区间的和全部加起来,为什么是效率是log(n)的呢?
以下给出证明:
n = n – lowbit(n)这一步实际上等价于将n的二进制的最后一个1减去。而n的二进制里最多有log(n)个1,所以查询效率是log(n)
3. 修改
修改一个节点,必须修改其所有祖先,最坏情况下为修改第一个元素,最多有log(n)个祖先
所以修改算法如下(给某个结点i加上x):
step1: 当i > n时,算法结束,否则转第二步;
step2: Ci = Ci + x, i = i + lowbit(i)转第一步。
(i = i +lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程)
(下图表示修改A数组中的第一个元素,对应的C数组应做的修改)
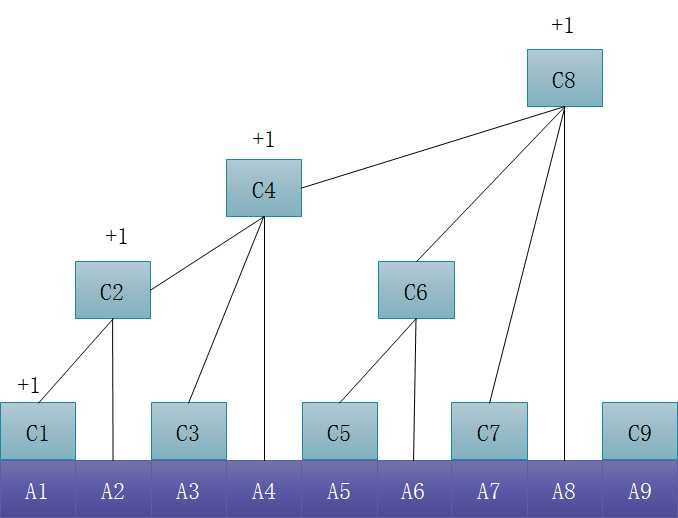
//计算2^k public int lowbit(int index) { int temp = index & (-index); return temp; }
/// <summary> /// 修改某一元素值后对树状数组的维护操作 /// </summary> /// <param name="index">需要修改元素的索引值</param> /// <param name="value">元素修改的增量</param> public void add(int index, int value) { while (index < A.Length) //A.Length为原数组的长度 { C[index] += value; index = lowbit(index); } }
/// <summary> /// 对A数组(原数组)进行预处理得到树状数组C /// </summary> public void pretreatment_AToC() { for (int i = 0; i < A.Length; i++) { add(i, A[i]); } }
/// <summary> /// 计算从0开始到索引值为index的元素之和 /// </summary> /// <param name="index">终止元素索引值</param> /// <returns></returns> public int sum(int index) { int s = 0; while (index > 0) { s += C[index]; index -= lowbit(index); } return s; }
/// <summary> /// 计算索引值从start到end的元素之和 /// </summary> /// <param name="start">起始元素索引值</param> /// <param name="end">结尾元素索引值</param> /// <returns></returns> public int sum_StartToEnd(int start, int end) { if (start == 0) { return sum(end); } return sum(end) - sum(start - 1); }
1. 题目描述(Color the ball):
N个气球排成一排,从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b <=N),小明从气球a开始到气球b依次给每个气球涂一次颜色。但是多次以后小明已经忘记了第 i 个气球已经涂过几次颜色了,你能帮他算出每个气球被涂过几次颜色吗?
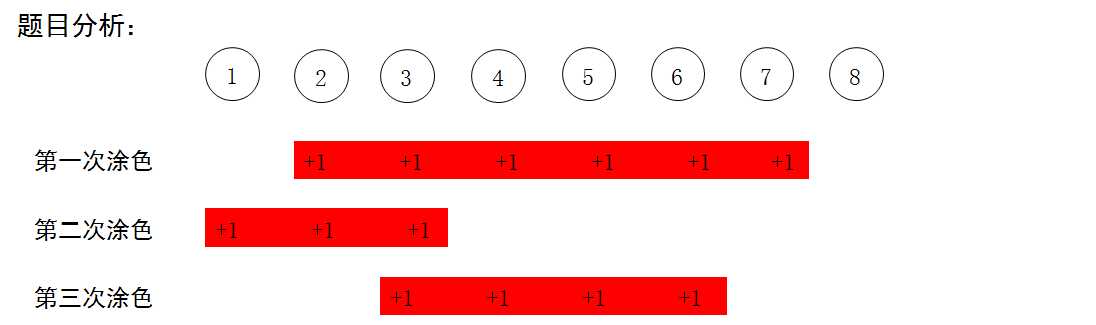
2. 思路
假设有8个气球,下面经过三次染色
采用向上更新,向下统计的方法:
树状数组中的每个节点都代表了一段线段区间,每次更新,根据其特性可以把起始点 a 以后包含的区间找出来,然后把 a 以后的区间全部加一次染色次数;再把 b 以前的区间全部减一次染色次数,这样就修改了树状数组中的[a,b]的区间染色次数。
3. 代码实现
static void Main(string[] args) { i = 3;//染色过程次数 Console.WriteLine("请输入气球的总个数:"); N = Int32.Parse(Console.ReadLine());//示例程序,暂不作异常处理,下同 Balloon = new int[N+1]; while (i > 0) { i--; Console.WriteLine("请输入起始位置:"); a = Int32.Parse(Console.ReadLine()); Console.WriteLine("请输入终点位置:"); b = Int32.Parse(Console.ReadLine()); add(a, 1);//从起始位置开始更新 add(b + 1, -1);//将终止位置后的元素的更新抵消 } Console.WriteLine("每个气球的被涂的次数为:"); for (int j = 1; j <= N; j++) { Console.Write(sum(j) + " ");//输出每个气球被染色的次数 } Console.ReadKey(); }
4. 输出

标签:adk 返回 rgs ati 构造 处理 增加 str 查询
原文地址:http://www.cnblogs.com/Lehman-Share/p/8004983.html