排序算法——Shell排序

二、Shell排序

　　Shell排序也叫“缩减增量排序”（disminishing increment sort），基于插入排序进行。

　　Shell建议的序列是一种常用但不理想的增量序列：1，...，N/8，N/4，N/2 （h_t=N/2,h_k=h_k+1/2）

void shellSort(vector<int> &a)
{
  for(int gap=a.size()/2;gap>0;gap/=2)
  {
    //对于hk（即gap），hk+1，...，N-1中的每个位置i，把位置i上的元素放到i,i-hk,i-2hk......中的正确位置上
    for(int i=gap;i<a.size();++i)
    {
      int tmp=a[i];
      int j=i;
      for(;j>=gap&&tmp<a[j-gap];j-=gap)
      {
        a[j]=a[j-gap];
      }
      a[j]=tmp;
    }          
}

思路：

　　通过比较相隔一定间隔（h_k）的元素来工作，各趟比较所用的距离随算法的进行而减小，直到只比较相邻元素的最后一趟排序为止。 

步骤：

　　使用一个增量序列h₁,h₂,...h_t，只要h₁=1，任何增量序列都是可行的。

　　1）先将待排元素序列分成若干个子序列（每个子序列由相隔某个“增量”的元素组成），分别进行插入排序； 

　　　  在使用增量h_k的一趟排序后，对每个i，都有a[i]≤a[i+h_k]，即所有相隔h_k的元素都被排序，此时称文件是h_k排序的； 

            一趟h_k排序的作用，即对h_k个独立子数组执行一次插入排序。      

          （希尔排序的一个重要性质——一个h_k排序的文件保持它的h_k排序性，不会被后面的各趟排序打破。）

　　2）依次缩减增量，再重复步骤 1）进行排序；

　　3）直到h_k为1时，再对全体元素进行一次直接插入排序（insertion sort）；

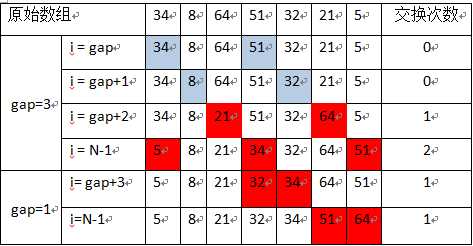
　　待排数组为{34,8,64,51,32,21,5}，数组大小N=7，则增量序列为1，3。

　　h_k=3时，对{34,51,5}，{8,32}，{64,21}这3个子数组进行插入排序（其中，每个数组元素相隔3），h_k=3 排序后的数组为{5,8,21,34,32,64,51}。

　　增量缩减为h_k=1，即对全体元素进行一次插入排序，排序完成，得到最终的有序数组为 {5,8,21,32,34,51,64}。

时间复杂度：

　　Shell排序的运行时间依赖于增量序列的选择，证明较为复杂。

　　使用Shell建议的增量序列：1，...，N/8，N/4，N/2 （h_t=N/2,h_k=h_k+1/2），最坏情形是Θ（N²）

　　使用Hibbard增量序列：1,3,7，......，2^k-1，最坏情形为Θ（N^3/2）.

适用情形：

　　普通的插入排序适用于非常少量的输入。

　　希尔排序在适量输入时是上佳选择，对适当的增量序列，性能极好，且代码少，易写。