一.基本概念

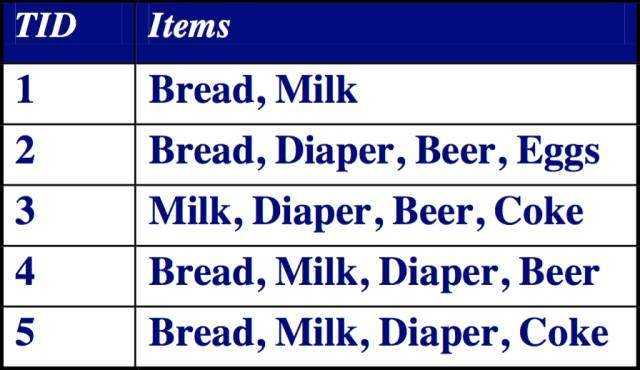
　　我们来看上面的事务库，如同上表所示的二维数据集就是一个购物篮事务库。该事物库记录的是顾客购买商品的行为。这里的TID表示一次购买行为的编号，items表示顾客购买了哪些商品。

　　事务：

　　事务库中的每一条记录被称为一笔事务。在上表的购物篮事务中，每一笔事务都表示一次购物行为。

　　项集(T)：

　　包含0个或者多个项的集合称为项集。在购物蓝事务中，每一样商品就是一个项，一次购买行为包含了多个项，把其中的项组合起来就构成了项集。

　　支持度计数：

　　项集在事务中出现的次数。例如，｛Bread，Milk｝这个项集在事务库中一共出现了3次，那么它的支持度计数就是3。

　　支持度(s)：

　　包含项集的事务在所有事务中所占的比例：上面的例子中我们得到了{Bread，Milk}这个项集的支持度计数是3，事物库中一共有5条事务，那么{Bread，Milk}这个项集的支持度就是3/5。

　　频繁项集：

　　如果我们对项目集的支持度设定一个最小阈值，那么所有支持度大于这个阈值的项集就是频繁项集。

　　关联规则：

　　在了解了上述基本概念之后，我们就可以引入关联分析中的关联规则了。

　　关联规则其实是两个项集之间的蕴涵表达式。如果我们有两个不相交的项集X和Y，就可以有规则X→Y, 例如｛Bread，Milk｝→{Diaper}。项集和项集之间组合可以产生很多规则，但不是每个规则都是有用的，我们需要一些限定条件来帮助我们找到强度高的规则。

　　支持度(s)：

　　关联规则的支持度定义为：也就是同时包含X和Y这两个项集的事务占所有事务的比例。我们看｛Bread，Milk｝→{Diaper}这个例子，同时包含｛Bread，Milk，Diaper}这个项集的事务一共有2项，因此这个规则的支持度是2/5。

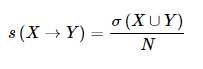
　　支持度很低的规则只能偶然出现，支持度通常用来删除那些无意义的规则。还具有一种期望的性质，可以用于关联规则的发现。

　　置信度(c)：

　　关联规则的置信度定义为：这个定义确定的是Y在包含X的事务中出现的频繁程度。还是看｛Bread，Milk｝→{Diaper}这个例子，包含｛Bread，Milk｝项的事务出现了2次，包含｛Bread，Milk，Diaper}的事务也出现了2次，那么这个规则的置信度就是1。

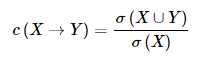
　　置信度度量通过规则进行推理具有可靠性。对于给定的规则，置信度越高，Y在包含X的事务中出现的可能性越大。置信度也可以估计Y在给定X的条件下概率。

　　对于关联规则定义这两个度量很有意义的。首先，通过对规则支持度支持度的限定滤去没有意义的规则。我们从商家的角度出发，数据挖掘意义是通过挖掘做出相应的战略决策产生价值。如果一个规则支持度很低，说明顾客同时购买这些商品的次数很少，商家针对这个规则做决策几乎没有意义。其次，置信度越大说明这个规则越可靠。

　　关联规则发现：

　　有了上述两个度量，就可以对所有规则做限定，找出对我们有意义的规则。首先对支持度和置信度分别设置最小阈值minsup和minconf。然后在所有规则中找出支持度≥minsup和置信度≥minconf的所有关联规则。给定事务集合T，关联规则发现是指找到支持度大于等于阈值minsup并且置信度大于等于minconf的所有规则。

　　有一点我们需要注意的是由简单关联规则得出的推论并不包含因果关系。我们只能由A→B得到A与B有明显同时发生的情况，但不能得出A是因，B是果。也就是说我们只能从案例中获得。

　　挖掘关联规则的一种原始方法是计算每个可能规则的支持度和置信度，但是代价很高。因此提高性能的方法是拆分支持度和置信度。因为规则的支持度主要依赖于X∪Y的支持度，因此大多数关联规则挖掘算法通常采用的策略是分解为两步：

　　频繁项集产生，其目标是发现满足具有最小支持度阈值的所有项集，称为频繁项集（frequent itemset）。

　　规则产生，其目标是从上一步得到的频繁项集中提取高置信度的规则，称为强规则（strong rule）。通常频繁项集的产生所需的计算远大于规则产生的计算花销。