三、归并排序(Merge Sort)
/** * 归并排序的驱动程序 */ void mergeSort(vector<int> &a) { vector<int> tmpArray(a.size()); mergeSort(a, tmpArray, 0, a.size() - 1); }

/** * 进行递归调用的内部方法 * a为待排序数组 * tmpArray为存放归并排序结果的数组 * left为子数组的最左元素的下标 * right为子数组最右元素的下标 */ void mergeSort(vector<int> &a, vector<int> &tmpArray, int left, int right) { if (left < right) { int center = (left + right) / 2; mergeSort(a, tmpArray, left, center); //左半部分序列 mergeSort(a, tmpArray, center + 1, right); //右半部分序列 merge(a, tmpArray, left, center + 1, right); } }

/** * 合并子数组已排序的两半部分 * leftPos:子数组最左元素的下标 * rightPos:后半部分起点的下标 * rightEnd:子数组最右元素的下标 */ void merge(vector<int> &a, vector<int> &tmpArray, int leftPos, int rightPos, int rightEnd) { int leftEnd = rightPos - 1; //左半部分末尾的位置 int tmpPos = leftPos; int numElements = rightEnd - leftPos + 1; /* 主循环:两区间段都未结束时 */ while (leftPos <= leftEnd && rightPos <= rightEnd) { if (a[leftPos] <= a[rightPos]) tmpArray[tmpPos++] = a[leftPos++]; else tmpArray[tmpPos++] = a[rightPos++]; } /* 复制前半部分的剩余元素 */ while (leftPos <= leftEnd) tmpArray[tmpPos++] = a[leftPos++]; /* 复制后半部分的剩余元素 */ while (rightPos <= rightEnd) tmpArray[tmpPos++] = a[rightPos++]; /* 将tmpArray复制回原数组a */ for (int i = 0; i < numElements; ++i) { a[rightEnd] = tmpArray[rightEnd]; //注:rightEnd未变 rightEnd--; } }
思路:“分治”
“分”:数组尽可能分,一直分到原子级别 ——logN
“并”:将原子级别的数两两归并排序,并产生最后结果 ——O(N)
——O(NlogN)
步骤:
1)基准情形:N=1,无需排序
2)N>1,递归地将前半部分数据a[left,...,center]和后半部分数据a[center+1,...,right]各自归并排序,再用合并算法将这两部分合在一起
3)合并算法:
取两个输入数组A,B,一个输出数组C,3个计数器pA,pB,pC,初始置于对应数组的头部;
A[pA]和B[pB]中的较小者被复制到C中的下一个位置,相关计数器向前推进一步;
当两个输入表中有一个用完时,将另一个表中剩余的部分复制到C中。
eg. 原始数组 {24,15,1,26,13,27,2,28}
拆分:
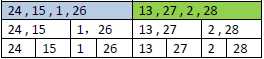
合并:
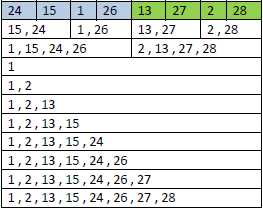
时间复杂度:
归并排序的运行时间为O(NlogN)
N=1,时间为常数,记为1。
N>1,用时为2T(N/2)+N(合并所花时间)
T(N) = 2T(N/2)+N
两边除以N,得到
T(N)/N=T(N/2)/(N/2)+1
T(N/2)/(N/2)=T(N/4)/(N/4)+1
......
T(2)/2=T(1)/1+1
相加可得 T(N) =NlogN+N =O(NlogN)
适用情形:
归并排序需要使用额外的内存(临时数组),且运行时间严重依赖于比较元素和在数组(及临时数组)中移动元素的相对开销,耗时,效率比不上快速排序。
但其使用的比较次数几乎是最优的,且实现简单,概念简单。

