参考资料
《算法(java)》 — — Robert Sedgewick, Kevin Wayne
《数据结构》 — — 严蔚敏
这篇文章主要介绍实现字典的两种方式
- 有序数组
- 无序链表
(二叉树的实现方案将在下一篇文章介绍)
【注意】 为了让代码尽可能简单, 我将字典的Key和Value的值也设置为int类型,而不是对象, 所以在下面代码中, 处理“操作失败”的情况的时候,是返回 -1 而不是返回 null 。 所以代码默认不能选择 -1作为 Key或者Value
(在实际场景中,我们会将int类型的Key替换为实现Compare接口的类的对象,同时将“失败”时的返回值从-1设为null,这时是没有这个问题的)
字典的定义和相关操作
字典又叫查找表(Search), 是由同一类型的数据元素构成的集合, 由于集合中的数据元素存在着完全松散的关系, 因此查找表是一种非常灵便的数据结构。
对查找表经常进行的操作有:
- 查询某个特定的数据是否在查找表中
- 检索某个特定的数据元素的各种属性
- 在查找表中插入一个数据元素
- 从查找表中删除某个数据元素
若对查找表只做1,2两种查找的操作, 这样的查找表被称为“静态查找表”
若在查找过程中同时还进行了3,4操作, 这样的查找表被称为“动态查找表”
有序数组实现字典
有序数组实现字典思路
字典,有最关键的两个类型的值: Key和Value。 但是一个数组显然只能存储一个类型的值呀, 正因如此:
首先,我们需要预备两个数组, 其次,我们要在每次操作中同步两个数组的状态。
1. 预备两个数组,一个存储Key, 一个存储Value


2. 在每次操作中同步两个数组的状态, 以有序数组的插入键值对的操作为例(put)

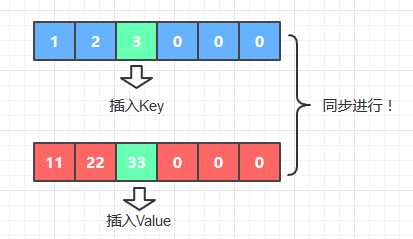
(int类型的数组初始化后,默认值是0)
Key和Value的位置是相同的
双数组实现字典功能的核心在于: 每一步操作里,Key和Value在两个数组里的位置是相同的, 这意为着你查找出Key的位置时, 也一并查找出了Value的位置。 例如删除操作时, 假设Key和Value的数组分别为a1和a2, 通过对Key的查找得出Key的位置是x, 那么接下来只要对a1[x]和a2[x] 同时进行操作就可以了
字典长度和数组长度
同时要注意一个简单却容易搞混的点:字典长度和数组长度是两个不一样的概念。
- 数组长度是创建后固定不变的,例如一开始就是N
- 字典的长度是可变的, 开始是0, 逐渐递增到N。
以有序数组为例

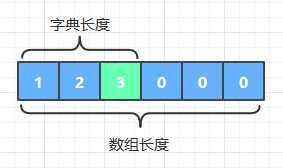
【注意】这里的“数组长度固定不变”是相对而言的, 下面我会介绍当字典满溢时扩建数组的操作(resize)
选择有序数组的原因
要实现字典, 使用有序数组和无序数组当然都可以, 让我们思考下: 为什么要选择有序数组呢?
有序数组相对于无序数组的性能优势
在实现上,无序数组和有序数组的性能差异, 本质上是顺序查找和二分查找的性能差异。
因为二分查找是基于有序数组的,所以
- 选择无序数组实现字典, 也就意味着选择了顺序查找。
- 而选择有序数组实现字典, 代表着你可以选择二分查找(或插值查找等), 并享受查找性能上的巨大提升。
关于顺序查找和二分查找的区别可以看下我的上一篇博客
三个成员变量,一个核心方法
我们使用的有序数组类的代码结构如下图所示:
(二分查找字典)
public class BinarySearchST { int [] keys; // 存储key int [] vals; // 存储value int N = 0; // 计算字典长度 public BinarySearchST (int n) { // 根据输入的数组长度初始化keys和vals keys = new int[n]; vals = new int[n]; } public int rank (int key) { // 查找Key的位置并返回 // 核心方法 } public void put (int key, int val) { // 通过一些方式调用rank } public int get (int key) { // 通过一些方式调用rank } public int delete (int key) { // 通过一些方式调用rank } }
三个成员变量: keys, vals, N
一个核心方法: rank (查找Key的位置),我们下面介绍的大多数方法都要依赖于调用rank去实现。
无序链表实现的字典API
1. rank方法
几乎所有基础的方法,例如get, put, delete都要依赖rank的调用来实现, 所以首先让我来介绍下rank的实现
rank方法的代码和普通的二分查找的代码基本相同, 但有一点区别。
普通的二分查找:
- 查找成功,返回Key的位置
- 查找失败(Key不存在),返回 - 1
对应rank方法的实现
- 查找成功,返回Key的位置
- 查找失败(Key不存在),返回小于给定Key的元素数量
为什么比起普通的二分查找,rank方法在后一点不是返回 -1 而是返回小于给定Key的元素数量呢? 因为对于某些调用rank方法,例如put方法来说,在Key不存在的时候也需要提供插入的位置信息, 所以当然不能只返回 -1了。
代码如下:
public int rank (int key) { int mid; int low= 0,high = N-1; while (low<=high) { mid = (low + high)/2; if(key<keys[mid]) { high = mid - 1; } else if(key>keys[mid]) { low = mid + 1; } else { return mid; // 查找成功,返回Key的位置 } } return low; // 返回小于给定Key的元素数量 }
关于普通二分查找的代码可以看下我的上一篇文章
2. put方法
put方法的参数
接收两个参数key和val, 表示要插入的键值对
put方法的实现思路
调用rank方法返回位置下标 i, 然后根据给定的key判断key == keys[i]是否成立
- 如果key等于keys[i],说明查找成功, 那么只要替换vals数组中的vals[i]为新的val就可以了,如图A
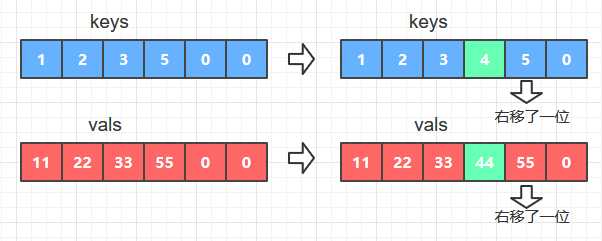
- 如果key不等于keys[i],那么在字典中插入新的 key-val键值对,具体操作是将数组keys和vals中大于给定key和val的元素全部右移一位, 然后使keys[i]=key; vals[i] = val; 如图B
如图所示:
图A

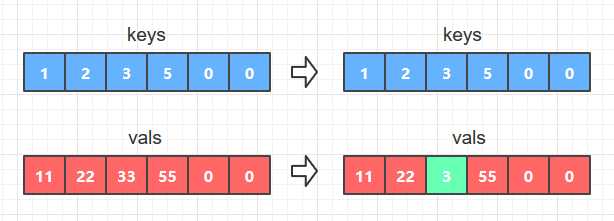
图B

代码如下:
public void put (int key, int val) { int i = rank(key); if(i<N&&key == keys[i]) { // 查找到Key, 替换vals[i]为val vals[i] = val; return ; // 返回 } for (int j=N;j>i;j-- ) { // 未查找到Key keys[j] = keys[j-1]; // 将keys数组中小于key的值全部右移一位 vals[j] = vals[j-1]; // 将vals数组中小于val的值全部右移一位 } keys[i] = key; // 插入给定的key vals[i] = val; // 插入给定的val N++; }
if(i<N&&key == keys[i]) 里的 i<N的作用是什么?
这个问题等价于: 不能直接用key == keys[i]作为判定条件吗。
根据上面rank方法中二分查找的代码可知, low和high交叉的时候,即刚好使low>high的时候,查找结束,所以查找结束时,low和high的关系可能是下面这种情况:
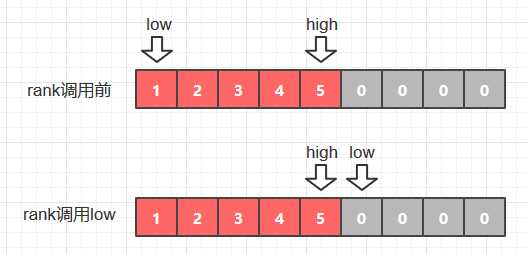

红色部分表示现有字典的长度, 图中low刚好 “越界”了,也即使low=N。(这里的N是字典的长度)。
keys[0] ~ keys[N-1]是存储key的元素, 而keys[N]则是尚未存储key的元素, 所以被默认初始化为0。
在上面的前提下, 如果这时key又刚好是0的话, key == keys[i] (i =N)将判定为 true, 这样就会对处在字典之外的vals[N]执行 vals[N] = 0的操作, 这显然是不正确的。
所以要添加i<N这个判断条件
for循环里的判断条件
for循环里执行的操作是: 将数组keys和vals中大于给定key和val的元素全部右移一位。
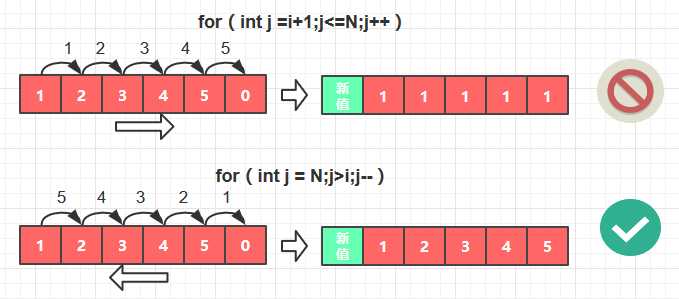
但是要注意, 右移一位的顺序是“从右到左”, 而不是“从左到右”,这意味着,我们不能把
for (int j=N;j>i;j-- ) { }
写成:
for (int j=i + 1;j<=N;j++ ) { }
因为这样做会导致key/val右边的元素变得完全一样的错误结果

3. get方法
输入参数为给定的key, 返回值是给定key对应的value值, 如果没有查找到key,则返回 -1, 提示操作失败。
要注意一点: 当 N = 0即字典为空的时候,显然不需要进行查找了, 可以直接返回 -1
代码如下:
public boolean isEmpty () { return N == 0; } // 判断字典是否为空(不是数组!) public int get (int key) { if(isEmpty()) return -1; // 当字典为空时,不需要进行查找,提示操作失败 int i = rank(key); if(i<N&&keys[i] == key) { return vals[i]; // 当查找成功时候, 返回和key对应的value值 } return -1; // 没有查找到给定的key,提示操作失败 }
4. delete方法
delete方法的实现结合了get方法和put方法部分思路
- 和get方法一样, 查找前要通过isEmpty判断字典是否为空,是则无需删除
- 和put方法类似, 删除要将keys/vals中大于key/value的元素全部“左移一位”
代码如下:
public int delete (int key) { if(isEmpty()) return -1; // 字典为空, 无需删除 int i = rank(key); if(i<N&&keys[i] == key) { // 当给定key存在时候,删除该key-value对 for(int j=i;j<=N-1;j++) { keys[j] = keys[j+1]; // 删除key vals[j] = keys[j+1]; // 删除value } N--; // 字典长度减1 return key; // 删除成功,返回被删除的key } return -1; // 未查找到给定key,删除失败 }
将keys/vals中大于key/value的元素全部“左移一位”的时候, delete方法和put方法的for循环的遍历方向是相反的。
不是
for (int j=N;j>i;j-- ) { }
而是
for(int j=i;j<=N-1;j++) { }
不要写错了, 不然会造成之前提到的“右边元素变得完全一样”的问题(这一点前面已经提过类似的点, 就不赘述了)
5. floor方法
输入key, 返回keys数组中小于等于给定key的最大值。
floor意为“地板”, 它指的是在字典中小于或等于给定值的最大值, 这听起来可能有点绕, 例如对字典1,2,3,4,5。 输入key为4,则对应的floor值是4; 而输入key为3.5,则对应的floor值为3。
实现的思路
首先要确认的是key是否存在
1. 如果输入的key存在, 则返回等于该key的keys元素即可
2. 若输入的key不存在, 则返回小于key的最大值: keys[rank(key)-1]
3. 在2中要注意一种特殊情况: 输入的key比字典中所有的元素都小, 这时显然找不到它的floor值,所以返回 -1, 表示操作失败
(假设rank = rank(key) ,三种情况如下图所示 )


public int floor (int key) { int k = get(key); // 查找key, 返回其value int rank = rank(key); // 返回给定key的位置 if(k!=-1) return key; // 查找成功,返回值为key else if(k==-1&&rank>0) return keys[rank-1]; // 未查找到key,同时给定key并没有排在字典最左端,则返回小于key的前一个值 else return -1; // 未查找到key,给定Key排在字典最左端,没有floor值 }
6. ceiling方法
输入key, 返回keys数组中大于等于给定key的最小值。
ceiling方法的实现思路和floor方法类似
实现的思路
首先要确认的是key是否存在
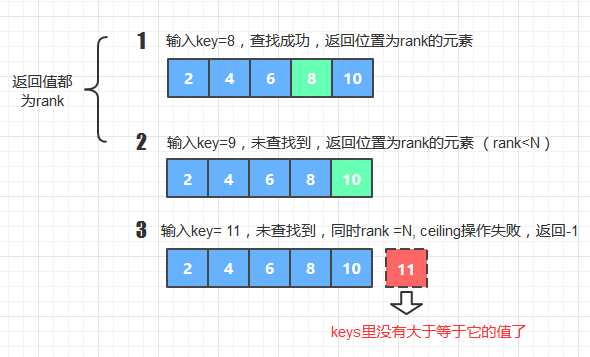
1. 如果输入的key存在, 则返回等于该key的keys元素即可, 即keys[rank(key)];
2. 若输入的key不存在, 则返回大于key的最大值: keys[rank(key)];
3. 在2中要注意一种特殊情况: 输入的key比字典中所有的元素都大, 这时显然找不到它的ceiling值,所以返回 -1, 表示操作失败
【注意】1,2中情况虽然不同,返回值却可以用同一个表达式,这和rank函数的编码有关
(假设rank = rank(key) ,三种情况如下图所示 )
代码
public int ceiling (int key) { int k = rank(key); if(k==N) return -1; return keys[k]; }

7. size方法
返回字典的大小, 即N
代码很简单:
public int size () { return N; }
之所以能直接返回,是因为我们在更改字典的操作时, 也相应地维护着N的状态
- 在声明N的时候初始化了: int N = 0;
- put操作完成时执行了N++
- delete操作完成时执行了N--;
8. max, min,select方法
public int max () { return keys[N-1]; } // 返回最大的key public int min () { return keys[0]; } // 返回最小的key public int select (int k) { // 根据下标返回key if(k<0||k>N) return -1; return keys[k]; }
9. resize
在我们的代码里, 字典长度是不断增长的,而数组长度是固定的, 那么这不由得让我们心生忧虑:
如果数组满了怎么办呢? 换句话说,从0增长的字典长度赶上了当前数组的长度。
因为java的数组长度在创建后不可调,所以我们要新建一个更大的数组,将原来的数组元素拷贝到新数组里面去。
因为字典涉及两个数组: keys和vals, 所以这里新建了两个新的临时数组tempKeys和tempVals, 转移完成后, 使得
keys = tempKeys;
vals = tempVals;
就可以了
private void resize (int max) { // 调整数组大小 int [] tempKeys = new int[max]; int [] tempVals = new int[max]; for(int i=0;i<N;i++) { tempKeys[i] = keys[i]; tempVals[i] = vals[i]; } keys = tempKeys; vals = tempVals; }
然后在put方法里加上:
// 字典长度赶上了数组长度,将数组长度扩大为原来的2倍 if(N == keys.length) { resize(2*keys.length) }
全部代码如下:
/** * @Author: HuWan Peng * @Date Created in 11:54 2017/12/10 */ public class BinarySearchST { int [] keys; int [] vals; int N = 0; public BinarySearchST (int n) { keys = new int[n]; vals = new int[n]; } public int size () { return N; } public int max () { return keys[N-1]; } // 返回最大的key public int min () { return keys[0]; } // 返回最小的key public int select (int k) { // 根据下标返回key if(k<0||k>N) return -1; return keys[k]; } public int rank (int key) { int mid; int low= 0,high = N-1; while (low<=high) { mid = (low + high)/2; if(key<keys[mid]) { high = mid - 1; } else if(key>keys[mid]) { low = mid + 1; } else { return mid; } } return low; } public void put (int key, int val) { int i = rank(key); if(i<N&&key == keys[i]) { // 查找到Key, 替换vals[i]为val vals[i] = val; return ; // 返回 } for (int j=N;j>i;j-- ) { // 未查找到Key keys[j] = keys[j-1]; // 将keys数组中小于key的值全部右移一位 vals[j] = vals[j-1]; // 将vals数组中小于val的值全部右移一位 } keys[i] = key; // 插入给定的key vals[i] = val; // 插入给定的val N++; } public boolean isEmpty () { return N == 0; } // 判断字典是否为空(不是数组!) public int get (int key) { if(isEmpty()) return -1; // 当字典为空时,不需要进行查找,提示操作失败 int i = rank(key); if(i<N&&keys[i] == key) { return vals[i]; // 当查找成功时候, 返回和key对应的value值 } return -1; // 没有查找到给定的key,提示操作失败 } public int delete (int key) { if(isEmpty()) return -1; // 字典为空, 无需删除 int i = rank(key); if(i<N&&keys[i] == key) { // 当给定key存在时候,删除该key-value对 for(int j=i;j<=N-1;j++) { keys[j] = keys[j+1]; // 删除key vals[j] = keys[j+1]; // 删除value } N--; // 字典长度减1 return key; // 删除成功,返回被删除的key } return -1; // 未查找到给定key,删除失败 } public int ceiling (int key) { int k = rank(key); if(k==N) return -1; return keys[k]; } public int floor (int key) { int k = get(key); // 查找key, 返回其value int rank = rank(key); // 返回给定key的位置 if(k!=-1) return key; // 查找成功,返回值为key else if(k==-1&&rank>0) return keys[rank-1]; // 未查找到key,同时给定key并没有排在字典最左端,则返回小于key的前一个值 else return -1; // 未查找到key,给定Key排在字典最左端,没有floor值 } }
无序链表
字典类的结构
public class SequentialSearchST { Node first; // 头节点 int N = 0; // 链表长度 private class Node { // 内部Node类 int key; int value; Node next; // 指向下一个节点 public Node (int key,int value,Node next) { this.key = key; this.value = value; this.next = next; } } public void put (int key, int value) { } public int get (int key) { } public void delete (int key) { } }
链表的组成单元是节点, 所以在 SequentialSearchST 类里面定义了一个匿名内部Node, 以便在外部类里能够实例化节点对象。
节点对象有三个实例变量: key,value和next, key和value分别用来存储字典的键和值, 而next用于建立节点和节点间的引用联系。
从头节点first开始, 依次将本节点的next实例变量指向下一个节点, 从而建立一条字典链表。

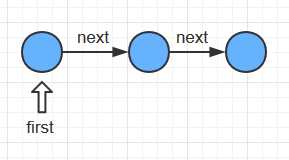
链表和数组在实现字典的不同点
1. 链表节点本身自带键和值属性, 所以用一条链表就能实现字典, 而数组要使用两个数组才可以
2. 数组通过增减下标值遍历元素, 而链表是依赖前后节点的引用关系进行迭代,从而实现节点的遍历
无序链表实现的字典API
1. put 方法
代码如下:
public void put (int key, int value) { for(Node n=first;n!=null;n=n.next) { // 遍历链表节点 if(n.key == key) { // 查找到给定的key,则更新相应的value n.value = value; return; } } // 遍历完所有的节点都没有查找到给定key // 1. 创建新节点,并和原first节点建立“next”的联系,从而加入链表 // 2. 将first变量修改为新加入的节点 first = new Node(key,value,first); N++; // 增加字典(链表)的长度 }
要理解
first = new Node(key,value,first);
这一句代码, 可以把它拆分成两段代码来看:
Node newNode = new Node(key,value,first); // 1. 创建新节点,并和原first节点建立“next”的联系 first = newNode // 2. 将first变量修改为新加入的节点
如图所示
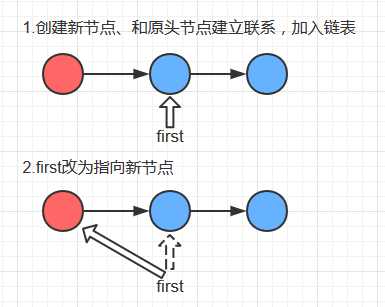

2. get方法
public int get (int key) { for(Node n=first;n!=null;n=n.next) { if(n.key==key) return n.value; } return -1; }
3. delete方法
public void delete (int key) { for(Node n =first;n!=null;n=n.next) { if(n.next.key==key) { n.next = n.next.next; N--; return ; } } }
关键代码
if(n.next.key==key) { n.next = n.next.next; }
的逻辑图示如下:
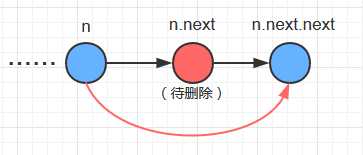

全部代码:
/** * @Author: HuWan Peng * @Date Created in 17:26 2017/12/10 */ public class SequentialSearchST { Node first; // 头节点 int N = 0; // 链表长度 private class Node { int key; int value; Node next; // 指向下一个节点 public Node (int key,int value,Node next) { this.key = key; this.value = value; this.next = next; } } public int size () { return N; } public void put (int key, int value) { for(Node n=first;n!=null;n=n.next) { // 遍历链表节点 if(n.key == key) { // 查找到给定的key,则更新相应的value n.value = value; return; } } // 遍历完所有的节点都没有查找到给定key // 1. 创建新节点,并和原first节点建立“next”的联系,从而加入链表 // 2. 将first变量修改为新加入的节点 first = new Node(key,value,first); N++; // 增加字典(链表)的长度 } public int get (int key) { for(Node n=first;n!=null;n=n.next) { if(n.key==key) return n.value; } return -1; } public void delete (int key) { for(Node n =first;n!=null;n=n.next) { if(n.next.key==key) { n.next = n.next.next; N--; return ; } } } }
有序数组和无序链表实现字典的性能差异
有序数组和无序链表的性能差异, 本质上还是顺序查找和二分查找的性能差异。 正因如此, 有序数组的性能表现远好于无序链表
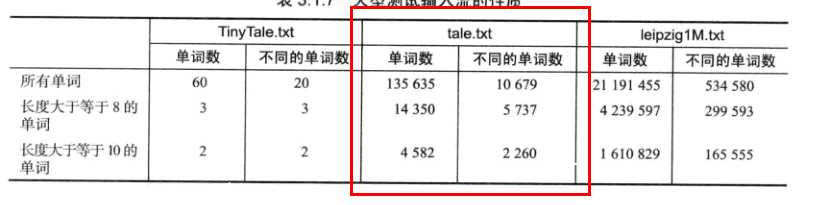
下面展示的是《算法》书中的测试结果,成本模型是对小说文本tale.txt中5737个不同的键执行put操作时,所用的总比较次数。(键是不同的单词,值是每个单词出现的次数)
无序链表实现的成本
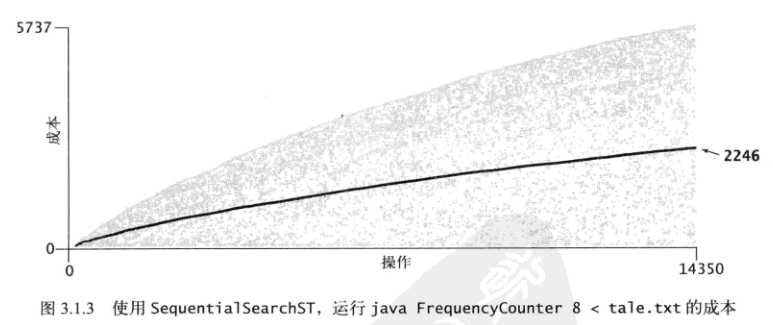

有序数组实现的成本

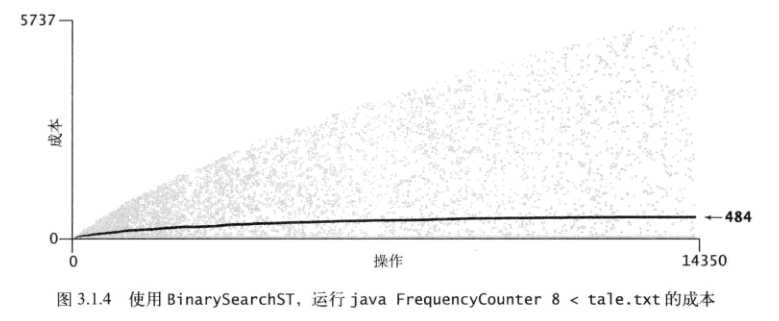
作为测试模型的tale.text的性质如下: