2017-2018-1 201552228 对分组密码的穷举攻击算法
算法概要:创新性地提出基于英文字母频率的稳定性,通过读取经过随机全排列处理的文本材料的英文字母来产生的随机序列作为穷举攻击的密钥
我们以DES算法为例对穷举攻击算法进行说明
DES算法采用64位主密钥,那么主密钥的密钥空间的密钥个数就是2^64,对每一个密钥的取值进行尝试是不现实的,因为计算机的运算能力有限,故从密钥空间中选取2^32个密钥进行尝试。实验的关键在于如何随机从2^64个密钥中随机取2^32个出来,换句话说就是如何在0~(2^64)-1中连续取2^32个值出来。
字母频率指的是各个字母在文本材料中出现的频率。在对大量文本材料进行考察统计后,每个字母的出现频率都将趋于稳定。通过来自于网络的多张字母频率表进行分析,发现只要能够保证文本材料来源广泛,单词数量足够多,每个字母的出现频率都是大同小异的。
首先我们对字母频率表中的字母进行分组,使得每一组中字母出现频率之和等于50%,如图所示。
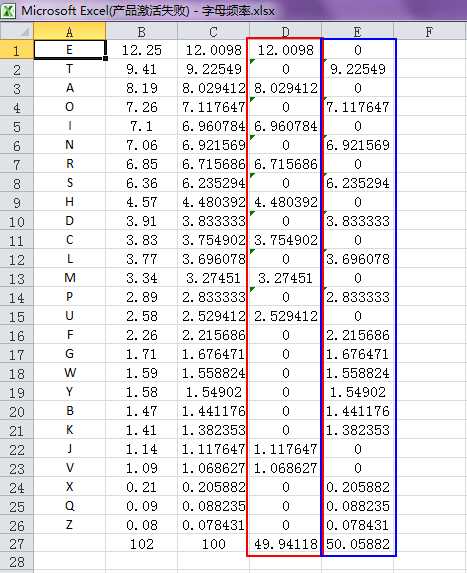
现在我们读取文本材料中任意一个字母,这个字母属于第一组的概率和属于第二组的概率是相等的,那么我们从文本材料中随机读取一个字符,就像抛一次硬币一样,出现正反面的概率是相等的。
然后我们需要准备文本材料并进行字符读取生成随机序列作为密钥。文本材料中的内容要足够多才行。我们需要2^32个密钥,每一个密钥的长度是2^6=64位,所以我们需要一个长度为2^38位的随机0-1序列。这个0-1序列就靠读取文本中的字母来获取,每次读取到一个字母就判断这个字母在第一组还是第二组,如果是在第一组就输出0,如果是在第二组就输出1。
一般情况下每个英文字母在计算机中是char类型变量,每个char类型的变量占1个字节,我们需要的随机序列的长度为2^32*64=274 877 906 944字节,也就是大约需要256G的文本数据。
我们现在来分析一下重复密钥的概率为1/(2^64)=5.4 * 10^(-20)远远小于数理统计中的小概率事件的标准0.05%,我们可以认为出现重复密钥是不会发生的。
我们直接按顺序读取文本材料的字母是不可以的,因为英文单词中的组合搭配并不是随机的,有的组合搭配会经常出现,比如说the,那么对应的三位0-1序列就会经常出现,而有的组合搭配就永远不会出现,比如说xyz,没有单词会使用这种搭配。这种英文单词的特点就造成了一种前后字母出现的牵连性。所以接下来我们要做的就是对文本材料的英文字母做一个随机全排列。这个实现起来并不复杂,密码学课程第一次实验的内容就是实现随机全排列。
生成0~n的全排列的思想:根据输入的n确定读入数据的字节数,然后将数据读入后进行根据数据的标号和数据的值进行计算确定需要交换位置的两个数,随后进行交换,即可得到P的一个全排列。
#include <stdio.h>
main ()
{
FILE *fp;
int a,b,c,d,i,j,n,temp;
int number[256]={0};
char ch;
char string[256];
if((fp=fopen("E:\\messages.txt","r"))==NULL)
{
printf("打开文件失败!\n");
exit(0);
}
else
{
printf("打开文件成功!\n");
}
printf("请输入n(不超过255):");
scanf("%d",&n);
b=0;
for(a=0;a<n;a++)
{
number[a]=a;
printf("%d ",number[a]);
b++;
if(b%10==0)
printf("\n");
}
printf("\n");
for(a=0;a<=n;a++)
{
string[a]=fgetc(fp);
}
for(i=n;i>0;i--)
{
j=(string[i-1]+string[i])%i;
temp=number[i];
number[i]=number[j];
number[j]=temp;
}
b=0;
for(a=0;a<n;a++)
{
printf("%d ",number[a]);
b++;
if(b%10==0)
printf("\n");
}
int fclose(FILE *fp);
在全排列生成完成之后,我们就可以开始逐个读取字母,根据字母所属的组来确定随机序列的下一位是0还是1。每生成64位随机序列,我们就用这个64位随机序列作为密钥对明文进行加密,将结果与密文进行比较,如果相同则说明这个64位随机序列就是真正的密钥,如果不相同就继续从文本中读取字母,生成随机序列,直到完成2^32次尝试为止。
