关于本文说明,本人原博客地址位于http://blog.csdn.net/qq_37608890,本文来自笔者于2017年12月12日 13:03:46所撰写内容(http://blog.csdn.net/qq_37608890/article/details/78738552)。
本文根据最近学习机器学习书籍 网络文章的情况,特将一些学习思路做了归纳整理,详情如下.如有不当之处,请各位大拿多多指点,在此谢过.
通过前两篇文章,我们对于k-近邻算法\決策树算法的分类问题有了有了解,通过这些分类器可以得到相应的決策,給出"该数据实例属于哪一类"這類問題的明確答案.但在深入研究過程中,我們會發現,分類器有時不可避免地產生錯誤的結果,這時就要求分類器給出一個最優的類別猜測結果,同時葉要給出這個猜測概率的估計值.這樣,基於概率論的分類方法之樸素貝葉斯就應運而生.
一 概述
1 概念理解
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
2 朴素贝叶斯分类工作原理
朴素贝叶斯分类工作原理:对于给出的待分类项,求解此项出现的条件下各个类别出现的概率,概率最大的那个类别就是待分类项所属的类别。比如,今天你看到一个人穿戴考究且有专职司机开豪车接送,你第一眼认为这哥们是个有钱人,为什么不猜他是个吊丝\乞丐呢?因为生活中拥有这样生活方式的人属于有钱的人概率最高,当然也不排出偶尔遇到一个吊丝花钱装逼一次刚好被看到,或者极个别乞丐真的很有钱的案例.但是在没有其他信息的情况下,我们会倾向于选择条件概率最大的哪个类别,这就是朴素贝叶斯的工作模式。
朴素贝叶斯分类的正式定义如下:
1、设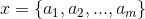 为一个待分类项,而每个a为x的一个特征属性。
为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合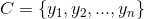 。
。
3、计算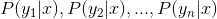 。
。
4、如果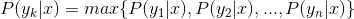 ,则
,则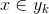 。
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即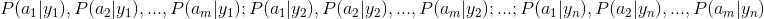 。
。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
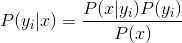
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
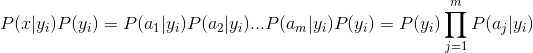
根据上述分析,朴素贝叶斯分类的流程可以由下图表示(暂时不考虑验证):
可以看到,整个朴素贝叶斯分类分为三个阶段:
第一阶段——准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段——分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
3 朴素贝叶斯的一般流程(通用流程)
(1)收集数据: 可以使用任何方法;
(2)准备数据: 需要布尔型或者数值型数据.
(3)分析数据: 有大量特征时,绘制特征作用不大,此时使用直方图效果更好.
(4)训练算法: 计算不同的独立特征的条件概率.
(5)测试算法: 计算错误率.
(6)使用算法: 可以在任意的分类场景中使用朴素贝叶斯分类器.
4 相关特性
优点:在数据较少的情况下仍然有效,可以处理多类别问题.
缺点:对于输入数据的准备方式较为敏感.
适用数据类型:标称型数据.
二 朴素贝叶斯算法场景
有一个装了 7 块石头的罐子,其中 3 块是白色的,4 块是黑色的。如果从罐子中随机取出一块石头,那么是白色石头的可能性是多少?由于取石头有 7 种可能,其中 3 种为白色,所以取出白色石头的概率为 3/7 。那么取到黑色石头的概率又是多少呢?很显然,是 4/7 。我们使用 P(white) 来表示取到白色石头的概率,其概率值可以通过白色石头数目除以总的石头数目来得到。
现在把这 7 块石头如下图所示,放在两个桶中,那么上述概率应该如何得到呢?
计算 P(white) 或者 P(black)
,如果事先我们知道石头所在桶的信息是会改变结果的。这就是所谓的条件概率(conditional probablity)。假定计算的是从 B
桶取到白色石头的概率,这个概率可以记作 P(white|bucketB) ,我们称之为“在已知石头出自 B
桶的条件下,取出白色石头的概率”。很容易得到,P(white|bucketA) 值为 2/4 ,P(white|bucketB) 的值为 1/3
。
条件概率的计算公式如下:
P(white|bucketB) = P(white and bucketB) / P(bucketB)
首先,我们用 B 桶中白色石头的个数除以两个桶中总的石头数,得到 P(white and bucketB) = 1/7 .其次,由于 B
桶中有 3 块石头,而总石头数为 7 ,于是 P(bucketB) 就等于 3/7 。于是又 P(white|bucketB) =
P(white and bucketB) / P(bucketB) = (1/7) / (3/7) = 1/3 。
另外一种有效计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即如果已知 P(x|c),要求 P(c|x),那么可以使用下面的计算方法:
三 示例: 皮马印第安人糖尿病分类预测案例
1 项目概述
该数据集是美国国立糖尿病、消化和肾脏疾病研究所(United States National Institute of Diabetes and Digestive and Kidney Diseases,简称NIDDK),通过所开发的皮马印第安人糖尿病数据集(Pima Indians Diabetes Data Set),发现:
令人吃惊的是,有超过30%的皮马人患有糖尿病。与此形成对照的是,美国糖尿病的患病率为8.3%,中国为4.2%。
这里采集数据包括768个对于皮马印第安患者的医疗观测细节,记录所描述的瞬时测量取自诸如患者的年纪,怀孕和血液检查的次数。所有患者都是21岁以上(含21岁)的女性,所有属性都是数值型,而且属性的单位各不相同。
数据集中的每个实例表示一个21岁以上(含21岁)的女性的信息,她属于以下两类之一,即5年内是否患过糖尿病,患者是否是在5年之内感染的糖尿病。如果是,则为1,否则为0。且每个人有8个属性,如下:
(1).怀孕次数。
(2).2小时口服葡萄糖耐量测试中得到的血糖浓度。
(3).舒张期血压(mm Hg)。
(4).三头肌皮脂厚度(mm)。
(5).2小时血清胰岛素(mu U/ml)。
(6).身体质量指数(体重kg/(身高in m)^2)。
(7).糖尿病家系作用。
(8).年龄。
机器学习文献中已经多次研究了这个标准数据集,好的预测精度为70%-76%.
2 朴素贝叶斯算法开发流程
2.1 下面给出了样本数据的样子(最后一列表示类别:0表示没有糖尿病,1表示有糖尿病)。
3 80 82 31 70 34.2 1.292 27 1 10 162 84 0 0 27.7 0.182 54 0 1 199 76 43 0 42.9 1.394 22 1 8 167 106 46 231 37.6 0.165 43 1 9 145 80 46 130 37.9 0.637 40 1 6 115 60 39 0 33.7 0.245 40 1 1 112 80 45 132 34.8 0.217 24 0 4 145 82 18 0 32.5 0.235 70 1 10 111 70 27 0 27.5 0.141 40 1 6 98 58 33 190 34 0.43 43 0
2.2 相关详细流程如下:
(1).处理数据:从CSV文件中载入数据,然后划分为训练集和测试集。
(2).提取数据特征:提取训练数据集的属性特征,以便我们计算概率并做出预测。
(3).单一预测:使用数据集的特征生成单个预测。
(4).多重预测:基于给定测试数据集和一个已提取特征的训练数据集生成预测。
(5).评估精度:评估对于测试数据集的预测精度作为预测正确率。
(6).合并代码:使用所有代码呈现一个完整的、独立的朴素贝叶斯算法的实现。
(1).处理数据
首先加载数据文件。CSV格式的数据没有标题行和任何引号。我们可以使用csv模块中的open函数打开文件,使用reader函数读取行数据。
我们也需要将以字符串类型加载进来属性转换为我们可以使用的数字。loadCsv()函数是用来加载匹马印第安人数据集(Pima indians dataset).
import csv
def loadCsv(filename):
lines = csv.reader(open(filename,"rt"))
dataset = list(lines)
for i in range(len(dataset)):
dataset[i] = [float(x) for x in dataset[i]]
return dataset
通过加载皮马印第安人数据集,然后打印出数据样本的个数,以此测试这个函数。
#输出并打印样本个数
filename = ‘pima-indians-diabetes.data.csv‘
dataset = loadCsv(filename)
print ((‘Loaded data file {0} with {1} rows‘).format(filename,len(dataset)))
#运行结果如下
Loaded data file pima-indians-diabetes.data.csv with 768 rows
下一步,我们将数据分为用于朴素贝叶斯预测的训练数据集,以及用来评估模型精度的测试数据集。我们需要将数据集随机分为包含67%的训练集合和包含33%的测试集(这是在此数据集上测试算法的通常比率)。splitDataset()函数以给定的划分比例将数据集进行划分。
#将样本数据集划分为用于朴素贝叶斯预测的训练数据集和用于评估模型精度的测试数据集。
#将样本数据随机划分为包含67%的训练数据集和33%的测试数据集。
import random
def splitDataSet(dataSet, splitRation):
trainSize = int(len(dataSet) * splitRatio)
copy = list(dataSet)
trainSet = []
while len(trainSet) < trainSize:
index = random.randrange(len(copy))
trainSet.append(copy.pop(index))
return [trainSet,copy]
# 假设一个有5个样例的样本集,将其分为训练数据集和测试数据集,并打印,看下每个样本数据最终落在哪个集合内。
dataSet = [[1],[2],[3],[4],[5]]
splitRatio =0.67
train,test = splitDataSet(dataSet, splitRatio)
print ((‘Split {0} rows into train with {1} and test with {2}‘).format(len(dataSet),train,test))
#运行结果如下:
Split 5 rows into train with [[5], [2], [3]] and test with [[1], [4]]
(2) 提取数据特征
朴素贝叶斯模型包含训练数据集中数据的特征,然后使用这个数据特征来做预测。
所收集的训练数据的特征,包含相对于每个类的每个属性的均值和标准差。举例来说,如果如果有2个类和7个数值属性,然后我们需要每一个属性(7)和类(2)的组合的均值和标准差,也就是14个属性特征。
在对特定的属性归属于每个类的概率做计算、预测时,将用到这些特征。
我们将数据特征的获取划分为以下的子任务:
- 按类别划分数据
- 计算均值
- 计算标准差
- 提取数据集特征
- 按类别提取属性特征
#按类别划分数据
#将训练数据集中的样本按照类别进行划分,计算出每个类别的统计数据。创建一个类别到属于此类别的样本列表的映射,并将整个数据集的样本分类到相应的映射列表。
#separateByClass()函数完成此项任务
def separateByClass(dataset):
separated = {}
for i in range(len(dataset)):
vector = dataset[i]
if (vector[-1] not in separated):
separated[vector[-1]] = []
separated[vector[-1]].append(vector)
return separated
#显然,函数假设样本中最后一个属性[-1]是类别值,返回一个类别值到数据样本列表的映射。
提供一些样本进行查看。
dataset = [[1,22,0],[2,25,0],[3,28,1],[4,35,0]]
separated = separateByClass(dataset)
print (("Separated instances into : {0}").format(separated))
#运行结果如下:
Separated instances into : {0: [[1, 22, 0], [2, 25, 0], [4, 35, 0]], 1: [[3, 28, 1]]}
#计算均值和标准差
#计算每个类中每个属性的均值。均值是数据的中点或数据集中趋势。在计算概率时,用它作为高斯分布中的中值。
#计算每个类中每个属性的标准差。标准差是数据散布的偏差。在计算概率时,用它来刻画高斯分布中,每个属性所期望的散布。
#这里采用N-1方法,即 属性值的个数减1。
import math
def mean(numbers):
return sum(numbers)/float(len(numbers))
def stdev(numbers):
avg = mean(numbers)
variance = sum([pow(x-avg,2)for x in numbers])/float(len(numbers)-1)
return math.sqrt(variance)/float(len(numbers))
#通过计算1到5的5个数的均值和标准差来测试
numbers = [1,2,3,4,5]
print((‘Summary :{0} ,mean: {1}, standed_vanriation : {2}‘).format(numbers,mean(numbers),stdev(numbers)))
#提取数据集特征
#现在可以提取数据集特征,对于一个给定的样本列表(对应于某个类),可以计算出每个属性的均值和标准差。
#Zip()函数可以将数据样本按照属性分组为一个个列表,然后可以对每个属性计算均值和标准差。
def summarize(dataset):
summarizes = [(mean(attribute),stdev(attribute)) for attribute in zip(*dataset)]
del summarizes[-1]
return summarizes
#可以用一些数据对于summarize()函数进行测试。
dataset = [[1,20,0],[2,21,1],[3,22,0]]
summarizes = summarize(dataset)
print ((‘Summarizes : {0}‘).format(summarizes))
#运行结果如下:
Summarizes : [(2.0, 0.3333333333333333), (21.0, 0.3333333333333333)]
#按类别提取属性特征
#先把训练数据集按类别进行划分,然后计算每个属性的摘要
def summarizeByClass(dataset):
separated = separateByClass(dataset)
summaries = {}
for classValue,instances in separated.items():
summaries[classValue] = summarize(instances)
return summaries
#使用一些数据进行测试
dataset = [[1,20,1],[2,21,0],[3,22,1],[4,22,0]]
summaries = summarizeByClass(dataset)
print ((‘Summary by class value : {0}‘). format(summaries))
#运行结果如下:
(3) 预测
我们现在可以使用从训练数据中得到的摘要来做预测。做预测涉及到对于给定的数据样本,计算其归属于每个类的概率,然后选择具有最大概率的类作为预测结果。
我们可以将这部分划分成以下任务:
- 计算高斯概率密度函数
- 计算对应类的概率
- 单一预测
- 评估精度
计算高斯概率密度函数
给定来自训练数据中已知属性的均值和标准差,我们可以使用高斯函数来评估一个给定的属性值的概率。
已知每个属性和类值的属性特征,在给定类值的条件下,可以得到给定属性值的条件概率。
关于高斯概率密度函数,可以查看参考文献。总之,我们要把已知的细节融入到高斯函数(属性值,均值,标准差),并得到属性值归属于某个类的似然(译者注:即可能性)。
在calculateProbability()函数中,我们首先计算指数部分,然后计算等式的主干。这样可以将其很好地组织成2行。
def calculateProbability(x, mean, stdev):
exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return (1/(math.sqrt(2*math.pi)*stdev))*exponent
#利用一些简单数据做测试
x = 71.5
mean = 73
stdev = 6.2
probability = calculateProbability(x, mean, stdev)
print ((‘Probability of belonging to this class : {0}‘). format(probability))
#运行结果如下:
Probability of belonging to this class : 0.06248965759370005# 计算所属类的概率
# 由前面内容可知,我们可以计算一个属性归属某个类的概率,那么合并数据样本中所有属性的概率,则可以得到整个数据样本归属某个类的概率。
# 使用乘法合并概率,在calculateClassProbabilities()函数中,给定数据样本,它属于每个类的概率,可以通过将其属性概率相乘得到。并
# 得到类别值到概率的映射。
def calculateClassProbabilities(summaries,inputVector):
probabilities = {}
for classValue, classSummaries in summaries.items():
probabilities[classValue] = 1
for i in range(len(classSummaries)):
mean, stdev = classSummaries[i]
x = inputVector[i]
probabilities[classValue] *= calculateProbability(x, mean,stdev)
return probabilities
# 利用一些简单数据做测试
summaries = {0:[(1,0.5)],1:[(20,5.0)]}
inputVector = [1.1,‘?‘]
probabilities = calculateClassProbabilities(summaries,inputVector)
print ((‘Probabilities for each class : {0}‘).format(probabilities))
#运行结果如下:
Probabilities for each class : {0: 0.7820853879509118, 1: 6.298736258150442e-05}
# 单一预测
# 既然可以计算一个数据样本归属每个类的概率,那么就可以找到概率的最大值,并返回关联的类。使用predict()函数。
def predict(summaries,inputVector):
probabilities = calculateClassProbabilities(summaries,inputVector)
bestLabel , bestProb = None, -1
for classValue, probability in probabilities.items():
if bestProb < probability or classValue is None:
bestProb = probability
bestLabel = classValue
return bestLabel
# 利用一些数据进行测试
summaries ={‘A‘:[(1,0.5)], ‘B‘:[(20,5.0)]}
inputVector = [1.1,‘?‘]
result = predict(summaries,inputVector)
print ((‘Prediction: {0}‘).format(result))
#运行结果如下:
Prediction: A
#多重预测
# 通过对测试数据中每个数据样本的预测,可以评估模型的精度。getPrediction()函数可以实现此功能,并返回每个测试数据样本的预测列表。
def getPredictions(summaries,testSet):
predictions = []
for i in range(len(testSet)):
result = predict(summaries, testSet[i])
predictions.append(result)
return predictions
#使用一些数据测试
summaries = {‘A‘:[(1.1,0.5)],‘B‘:[(0,5.0)]}
testSet = [[1.1,‘?‘],[19.8,‘?‘]]
predictions = getPredictions(summaries,testSet)
print ((‘Predicitons:{0}‘).format(predictions))
(4)模型精度评估
#计算精度
#通过计算得来的预测值与测试数据集中的类别值进行对比,可以得到一个介于0%~100%精确率作为类别的精确度。
def getAccuracy(testSet,predictions):
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] ==predictions[x]:
correct +=1
return (correct/(len(testSet)))*100.0
#使用一些数据进行测试
testSet = [[1,1,1,‘a‘],[2,2,2,‘a‘],[3,3,3,‘b‘]]
predictions =[‘a‘,‘a‘,‘a‘]
accuracy = getAccuracy(testSet, predictions)
print((‘Accuracy:{0}‘).format(accuracy))
Accuracy:66.66666666666666
(5) 合并代码: 梳理完以上思路之后,接下来我们来进行查看代码实现效果,详情如下:(注意,作者是在Python3下运行的,并运行成功)
# Example of Naive Bayes implemented from Scratch in Python
import csv
import random
import math
def loadCsv(filename):
lines = csv.reader(open(filename, "rt"))
dataset = list(lines)
for i in range(len(dataset)):
dataset[i] = [float(x) for x in dataset[i]]
return dataset
def splitDataset(dataset, splitRatio):
trainSize = int(len(dataset) * splitRatio)
trainSet = []
copy = list(dataset)
while len(trainSet) < trainSize:
index = random.randrange(len(copy))
trainSet.append(copy.pop(index))
return [trainSet, copy]
def separateByClass(dataset):
separated = {}
for i in range(len(dataset)):
vector = dataset[i]
if (vector[-1] not in separated):
separated[vector[-1]] = []
separated[vector[-1]].append(vector)
return separated
def mean(numbers):
return sum(numbers)/float(len(numbers))
def stdev(numbers):
avg = mean(numbers)
variance = sum([pow(x-avg,2) for x in numbers])/float(len(numbers)-1)
return math.sqrt(variance)
def summarize(dataset):
summaries = [(mean(attribute), stdev(attribute)) for attribute in zip(*dataset)]
del summaries[-1]
return summaries
def summarizeByClass(dataset):
separated = separateByClass(dataset)
summaries = {}
for classValue, instances in separated.items():
summaries[classValue] = summarize(instances)
return summaries
def calculateProbability(x, mean, stdev):
exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return (1 / (math.sqrt(2*math.pi) * stdev)) * exponent
def calculateClassProbabilities(summaries, inputVector):
probabilities = {}
for classValue, classSummaries in summaries.items():
probabilities[classValue] = 1
for i in range(len(classSummaries)):
mean, stdev = classSummaries[i]
x = inputVector[i]
probabilities[classValue] *= calculateProbability(x, mean, stdev)
return probabilities
def predict(summaries, inputVector):
probabilities = calculateClassProbabilities(summaries, inputVector)
bestLabel, bestProb = None, -1
for classValue, probability in probabilities.items():
if bestLabel is None or probability > bestProb:
bestProb = probability
bestLabel = classValue
return bestLabel
def getPredictions(summaries, testSet):
predictions = []
for i in range(len(testSet)):
result = predict(summaries, testSet[i])
predictions.append(result)
return predictions
def getAccuracy(testSet, predictions):
correct = 0
for i in range(len(testSet)):
if testSet[i][-1] == predictions[i]:
correct += 1
return (correct/float(len(testSet))) * 100.0
def main():
filename = ‘pima-indians-diabetes.data.csv‘
splitRatio = 0.67
dataset = loadCsv(filename)
trainingSet, testSet = splitDataset(dataset, splitRatio)
print((‘Split {0} rows into train={1} and test={2} rows‘).format(len(dataset), len(trainingSet), len(testSet)))
# prepare model
summaries = summarizeByClass(trainingSet)
# test model
predictions = getPredictions(summaries, testSet)
accuracy = getAccuracy(testSet, predictions)
print((‘Accuracy: {0}%‘).format(accuracy))
main()</span>
执行效果不错,结果如下:
Split 768 rows into train=514 and test=254 rows Accuracy: 74.40944881889764%
四 小结
截止目前,我们按照步骤实现了高斯版本的朴素贝叶斯。对于以后的扩展,可以视情况继续进行。
对于分类而言,使用概率有时比使用硬规则更有效。贝叶斯及贝叶斯准则提供了一种利用已知值来估计未知概率的有效方法。
利用现代编程语言来实现朴素贝叶斯时需要考虑很多实际因素。下溢出就是其中一个问题,它可以通过对概率取对数来解决。
后续有机会希望对于文档分类做些梳理研究,重点研究下词袋模型和词集模型在解决文档分类上面的效果情况。




