最大公约数:
如果数a能被数b整除,a就叫做b的倍数,b就叫做a的约数。
几个整数中公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
12、16的公约数有1、2、4,其中最大的一个是4,4是12与16的最大公约数,一般记为(12,16)=4。
公约数的用途就是约分:
把一个分数的分子和分母同时除以它们的公约数,分数的值不变,这个过程就叫约分;
约分让这个分数用起来更简单
最小公倍数:
几个自然数公有的倍数,叫做这几个数的公倍数,其中最小的一个自然数,叫做这几个数的最小公倍数。
4的倍数有4、8、12……,6的倍数有6、12、18……,4和6的公倍数有12、24,……,其中最小的是12。
一般记为[4,6]=12。
公倍数的用途就是通分:
把几个异分母分数化成与原来分数相等的同分母的分数的过程,叫做通分。
如果你想对两个分数进行加减运算,那么最好让他变成分母相同的两个分数,才方便计算。
这时候你可以找出这两个分数的分母的最小公倍数,然后就有办法做了。
数学归纳法
数学归纳法是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。
除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。
这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。
在数论中,数学归纳法是以一种不同的方式来证明任意一个给定的情形都是正确的(第一个,第二个,第三个,一直下去概不例外)的数学定理。
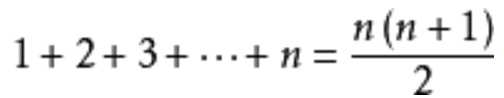
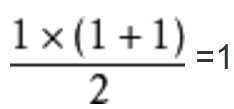
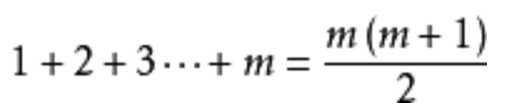 (等式1)
(等式1)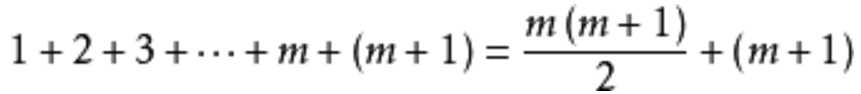 (等式2)
(等式2)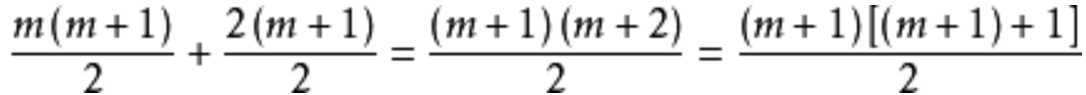
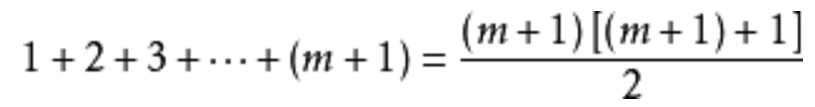
在数论中,数学归纳法是以一种不同的方式来证明任意一个给定的情形都是正确的(第一个,第二个,第三个,一直下去概不例外)的数学定理。
虽然数学归纳法名字中有“归纳”,但是数学归纳法并非不严谨的归纳推理法,它属于完全严谨的演绎推理法。
事实上,所有数学证明都是演绎法。
最简单和常见的数学归纳法是证明当n等于任意一个自然数时某命题成立。证明分下面两步:
- 证明当n= 1时命题成立。
- 假设n=m时命题成立,那么可以推导出在n=m+1时命题也成立。(m代表任意自然数)
当这两点都已经证明,那么任意值都可以通过反复使用这个方法推导出来。
下面做一道数学题:
举例证明下面的定理:
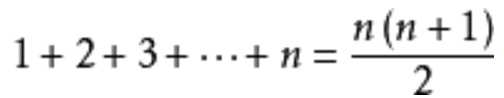
第一步,验证该公式在 n = 1 时成立。即有左边=1,右边
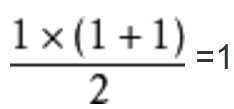
所以这个公式在n = 1时成立。
第二步,需要证明假设n = m 时公式成立,那么可以推导出n = m+1 时公式也成立。步骤如下:假设n = m 时公式成立,
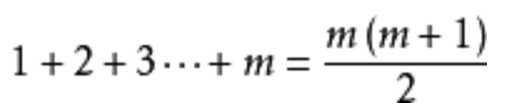 (等式1)
(等式1) 然后在等式两边同时分别加上m + 1 得到
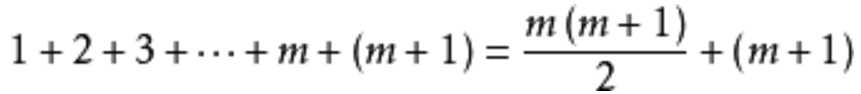 (等式2)
(等式2)这就是n = m+1 时的等式。我们下一步需要根据 等式1证明 等式2 成立。通过因式分解合并,
等式2的右边 :
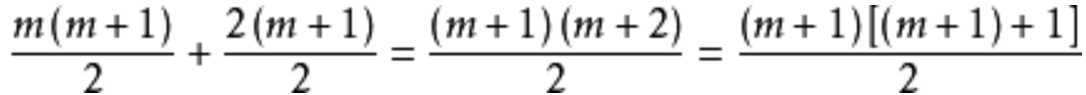
也就是:
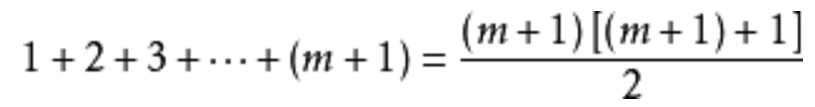
这样我们就完成了由n=m成立推导出n=m+1成立的过程,证毕。
结论:对于任意自然数n,公式均成立。