1.单刀直入
基数排序是基于多关键字的一种排序,借助“分配”与“收集”两个过程来得到一个有序序列,其时间复杂度为O(d(n+rd)),空间复杂度为O(n+rd),属于稳定的排序...
举个例子,加入有一下待排序列#->278->109->63->930->589->184->505->269->8->83(#为头节点,其他为数据节点)
依次序列,我们可以容易得到一下信息:
rd:rd在这里指的是十进制的十,即rd = 10(but,如果是在一字母序列中,例如#->‘C‘->‘A‘->‘B‘->‘F‘这里rd指的就是二十六进制,即rd = 26)
d: d在这里指的是序列中最大值的位数,很容易得到此序列中的最大值为930,是一个三位数,即d = 3
2.过程简介
接上,待排序列为:
#->278->109->63->930->589->184->505->269->8->83
接下来,我们就需开始进行第一趟分配(按个位分配),建立是rd个队列或者是rd个链表(以下前面的0,1,2.。。。9都是链表序号):
注意:按个位分配的意思就是:例如278的个位就是8,就把它放入第8号链表;109的个位是9,就把它放入第9号链表;依次类推。。。
0->930
1
2
3->63->83
4->184
5->505
6
7
8->278->8
9->109->589->269
分配后,开始第一趟收集(这里收集就是从0号链表开始收集到9号链表结束):
#->930->63->83->184->505->278->8->109->589->269
第二趟分配(按十位分配):
0->505->109->8
1
2
3->930
4
5
6->63->269
7->278
8->83->184->589
9
第二趟收集:
#->505->109->8->930->63->269->278->83->184->589
第三趟分配(按百位分配):
0->8->63->83
1->109->184
2->269->278
3
4
5->505->589
6
7
8
9->930
第三次收集:
#->8->63->83->109->184->269->278->505->589->930
排序完成。。。
3.其实思路就是那样,不过代码因人而异,拿什么数据结构去实现就可以达到不同的效果,但结果都可以使之有序,下面给出参考代码
1 #include <bits/stdc++.h> 2 #define SIZE 0x32 3 #define rd 10 4 using namespace std; 5 typedef struct snode{ 6 int key; 7 struct snode* next;//下位指针 8 } *sRadix; 9 typedef struct bnode{ 10 sRadix d[SIZE];//最大长度 11 int length;//实际长度 12 } bRadix; 13 int a[] = {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000};//辅助下标数组 14 int getPos(int value, int pos);//获得下标 15 void radixSort(bRadix &rl);//基数排序 16 void printL(bRadix rl);//打印收集链表 17 void printC(bRadix r);//打印分配过程 18 int main(){ 19 bRadix rl;//收集主链表 20 bRadix la;//运动链表 21 cout << "- - - - - - - - -1.基数排序- - - - - - - - -\n"; 22 cout << "请输入需排序的序列的长度:\n"; 23 cin >> rl.length; 24 cout << "初始化收集表..."; 25 rl.d[rl.length] = new snode; 26 rl.d[rl.length]->next = NULL; 27 la = rl; 28 cout << "请输入序列的元素集合:\n"; 29 for(int i = 0; i < rl.length; i++){//初始化收集链表 30 sRadix p = new snode; 31 cin >> p->key; 32 p->next = la.d[rl.length]->next; 33 la.d[rl.length]->next = p; 34 la.d[rl.length] = p; 35 } 36 radixSort(rl); 37 cout << "进过排序后的序列如下...\n"; 38 printL(rl); 39 return 0; 40 } 41 int getPos(int value, int pos){ 42 return value / a[pos - 1] % 10; 43 } 44 void radixSort(bRadix &rl){ 45 int maxValue = 0, d = 1; 46 bRadix r; 47 r.length = rl.length; 48 r.d[r.length] = rl.d[rl.length]; 49 while(r.d[rl.length]->next){ 50 if(r.d[rl.length]->next->key > maxValue) 51 maxValue = r.d[rl.length]->next->key; 52 r.d[rl.length] = r.d[rl.length]->next; 53 } 54 for(int i = 1; i < rd; i++) 55 if(maxValue / a[i] == 0) break; 56 else d++; 57 for(int i = 1; i <= d; i++){ 58 printf("- - - - - - - - -第%d次分配- - - - - - - - -\n", i); 59 bRadix r2, r0; 60 r0.length = r2.length = rl.length; 61 r0.d[r0.length] = r2.d[r2.length] = rl.d[rl.length]; 62 for(int k = 0; k < rl.length; k++){ 63 r0.d[k] = r2.d[k] = new snode; 64 r0.d[k]->next = r2.d[k]->next = NULL; 65 } 66 while(r0.d[r0.length]->next){ 67 int key = r0.d[rl.length]->next->key; 68 int pos = getPos(key, i); 69 for(int j = 0; j < rd; j++){ 70 if(pos == j){ 71 sRadix p = new snode; 72 p->key = key; 73 p->next = r0.d[j]->next; 74 r0.d[j]->next = p; 75 r0.d[j] = p; 76 j = rd; 77 } 78 } 79 r0.d[r0.length] = r0.d[r0.length]->next; 80 } 81 printC(r2); 82 for(int j = 0; j < rd; j++){ 83 if(r2.d[j]){ 84 while(r2.d[j]->next){ 85 int key = r2.d[j]->next->key; 86 r2.d[rl.length]->next->key = key; 87 r2.d[j] = r2.d[j]->next; 88 r2.d[rl.length] = r2.d[rl.length]->next; 89 } 90 } 91 } 92 } 93 cout << "- - - - - - - - -排序结束- - - - - - - - -\n"; 94 } 95 void printL(bRadix rl){ 96 while(rl.d[rl.length]->next){ 97 cout << rl.d[rl.length]->next->key << " "; 98 rl.d[rl.length] = rl.d[rl.length]->next; 99 } 100 cout << endl; 101 } 102 void printC(bRadix r){ 103 for(int i = 0; i < rd; i++){ 104 printf("#(%d)", i); 105 if(r.d[i]){ 106 while(r.d[i]->next){ 107 cout << "->" << r.d[i]->next->key; 108 r.d[i] = r.d[i]->next; 109 } 110 } 111 cout << endl; 112 } 113 }
效果图如下(包含上述分配与收集过程):
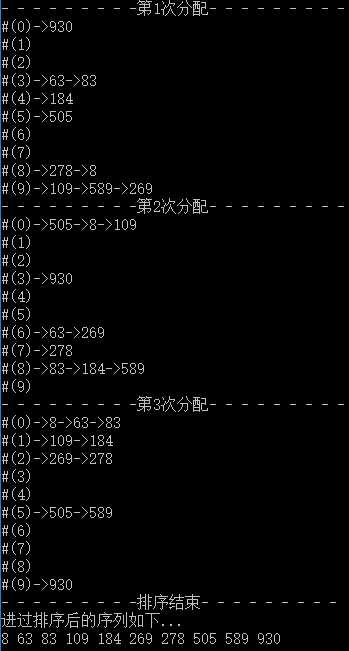
4.没懂的地方请在下边评论区留言,我会尽量为大家解答的。。。希望大家支持
