目录
基本信息
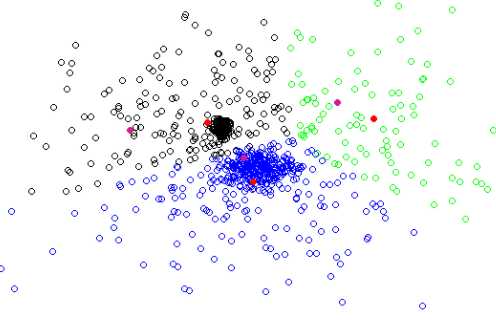
K-means算法是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
工作原理
从n个数据对象任意选择 k 个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然 后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到聚类中心K个对象不在更换为止。k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
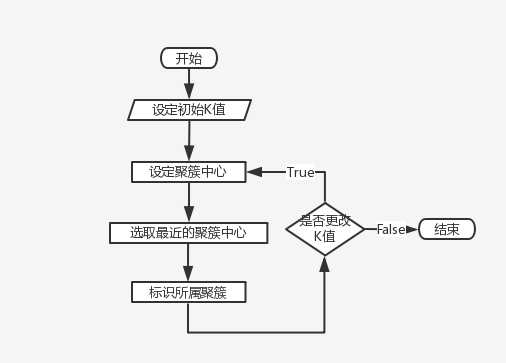
算法优缺点
K-Means聚类算法的优点主要集中在:
- 算法快速、简单
- 对大数据集有较高的效率并且是可伸缩性的
- 时间复杂度接近于线性,而且适合挖掘大规模数据集,K-Means聚类算法的时间复杂度是O(nkt),其中n代表数据集中对象的数量,t代表着算法迭代的次数,k代表着簇的数目。
K-Means算法的缺点
- 很多时候,事先并不知道给定的数据集应该分成多少个类才最合适。在算法中K是事先给定的,对聚类结果有较大的影响,一旦初始值选择不好,可能得到有效的聚类结果,对于该问题的解决,许多算法采用遗传算法,对于数据是密集的,簇与簇之间区别较明显,得到的聚类结果较为有效。
- 该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进,提高算法应用范围
算法实现
例如:如下随机生成1-100内10个double类型的数,可以看出数据簇与簇之间区别较为明显,得到的聚类较为有效,结果也比较明显。
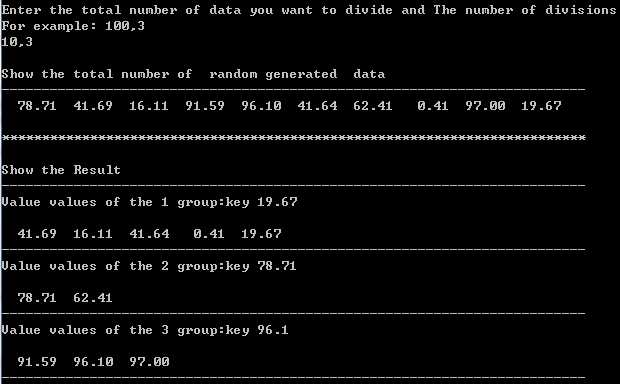
如下:随机生成100个数
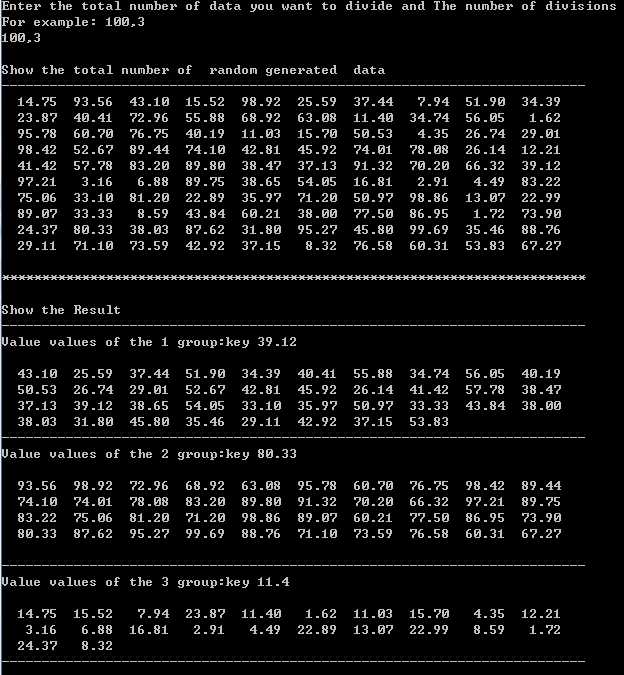
代码:
1 namespace DataStructure 2 { 3 using System; 4 using System.Collections.Generic; 5 /// <summary> 6 /// author yanhf 7 /// K-Means 8 /// </summary> 9 public class K_Means 10 { 11 /// <summary> 12 /// Update index cluster identification based on cluster point key 13 /// </summary> 14 /// <param name="data">Data</param> 15 /// <param name="index">index</param> 16 /// <param name="key">key values</param> 17 public static void _K_Means(double[] data, ref int[] index, int[] key) 18 { 19 bool change = true; 20 int _index = 0; 21 double Length = 0; 22 while (change) 23 { 24 change = false; 25 for (int i = 0; i < data.Length; i++)//根据当前的聚簇点更新index聚簇标识数组 26 { 27 for (int j = 0; j < key.Length; j++) 28 { 29 double currentLength = Math.Abs(data[key[j]] - data[i]); 30 if (j == 0 || Length > currentLength) 31 { 32 Length = Math.Abs(data[key[j]] - data[i]); 33 _index = j + 1; 34 } 35 } 36 index[i] = _index; 37 Length = 0; 38 } 39 change = _ChangeKey(data, index, ref key); 40 } 41 } 42 /// <summary> 43 /// Judging the current Key needs not to be changed 44 /// </summary> 45 /// <param name="data">Data</param> 46 /// <param name="index">index</param> 47 /// <param name="key">key values</param> 48 /// <returns></returns> 49 public static bool _ChangeKey(double[] data, int[] index, ref int[] key) 50 { 51 bool IsChange = false; 52 int i = 0; 53 List<double> _listData = new List<double>(); 54 while (i++ < key.Length) 55 { 56 _listData.Clear(); 57 for (int j = 0; j < index.Length; j++) 58 { 59 if (index[j] == i) 60 { 61 _listData.Add(data[j]); 62 } 63 } 64 _listData.Sort(); 65 if (_listData.Count > 1) 66 { 67 if (key[i - 1] != _index(data, _listData[_listData.Count / 2])) 68 { 69 IsChange = true; 70 key[i - 1] = _index(data, _listData[_listData.Count / 2]); 71 } 72 } 73 } 74 return IsChange; 75 } 76 /// <summary> 77 /// Get the index in the key‘s data 78 /// </summary> 79 /// <param name="data">Data</param> 80 /// <param name="num">key values</param> 81 /// <returns></returns> 82 public static int _index(double[] data, double num) 83 { 84 List<double> _listData = new List<double>(data); 85 return _listData.IndexOf(num) >= 0 ? _listData.IndexOf(num) : -1; 86 } 87 } 88 }
1 using DataStructure; 2 using System; 3 4 namespace ClusterNumeric 5 { 6 class ClusterNumProgram 7 { 8 public static int dataNumber = 0; 9 public static int keyNumber = 0; 10 static void Main(string[] args) 11 { 12 start: 13 string[] inputArray = null; 14 { 15 Console.WriteLine("\nEnter the total number of data you want to divide and The number of divisions\nFor example: 100,3"); 16 string input = Console.ReadLine(); 17 inputArray = input.Split(new char[] { ‘,‘ }); 18 } while (!int.TryParse(inputArray[0], out dataNumber) || !int.TryParse(inputArray[1], out keyNumber) || keyNumber >= dataNumber) ; 19 20 Random random = new Random(); 21 double[] _data = new double[dataNumber]; 22 Console.WriteLine("\nShow the total number of random generated data"); 23 Console.WriteLine("-------------------------------------------------------------------------"); 24 int M = 1; 25 for (int i = 0; i < _data.Length; i++) 26 { 27 _data[i] = Math.Round(random.NextDouble() * (100 < dataNumber ? dataNumber : 100), 2); 28 Console.Write(_data[i].ToString("F2").PadLeft(7)); 29 if (M++ % 10 == 0) 30 { 31 Console.WriteLine(); 32 } 33 } 34 int[] _index = new int[dataNumber]; 35 int[] keyData = new int[keyNumber]; 36 for (int i = 0; i < keyNumber; i++) 37 { 38 keyData[i] = random.Next(0, dataNumber); 39 } 40 K_Means._K_Means(_data, ref _index, keyData); 41 Console.WriteLine("\n*************************************************************************"); 42 Console.WriteLine("\nShow the Result"); 43 Console.WriteLine("-------------------------------------------------------------------------"); 44 for (int i = 0; i < keyData.Length; i++) 45 { 46 M = 1; 47 Console.WriteLine("Value values of the " + (i + 1) + " group:key " + _data[keyData[i]].ToString().PadRight(7)); 48 Console.WriteLine(); 49 for (int j = 0; j < _index.Length; j++) 50 { 51 if (_index[j] == i + 1) 52 { 53 Console.Write(_data[j].ToString("F2").PadLeft(7)); 54 if (M++ % 10 == 0) 55 { 56 Console.WriteLine(); 57 } 58 } 59 } 60 Console.WriteLine(); 61 Console.WriteLine("-------------------------------------------------------------------------"); 62 } 63 Console.WriteLine("*************************************************************************"); 64 goto start; 65 } 66 } 67 }
