下面通过一个简单的例子说明一下:如下图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
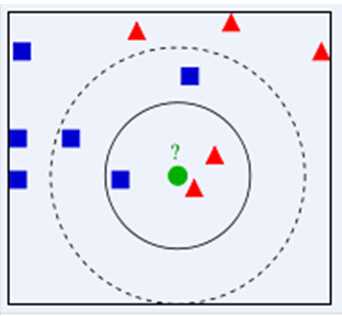
由此也说明了KNN算法的结果很大程度取决于K的选择
在KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,避免了对象之间的匹配问题,在这里距离一般使用欧氏距离或曼哈顿距离:

同时,KNN通过依据k个对象中占优的类别进行决策,而不是单一的对象类别决策。这两点就是KNN算法的优势。
接下来对KNN算法的思想总结一下:就是在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类,其算法的描述为:
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类
缺点:
1)没有建立模型,测试样本和预测样本都要与所有的训练样本比较,当训练集合测试集数据规模很大时,计算量会很大;
2)K近邻并不能给出一个可以理解的模型,不生成模型。
注意:计算样本与样本之间的相似度(或者距离)。由于样本的类别是由K近邻中最经常出现的类别决定的,注意K 的取值问题。注意 k=1 的情况下并不能足以决定测试样本的类别,因为数据有噪声和异常值(outliers)。需要多一些的近邻集合来准确的决定类别。
参考博客:
https://www.cnblogs.com/ybjourney/p/4702562.html
《Web数据挖掘》(第二版) Bing Liu 著 俞勇等译 -------------------------------(第三章 监督学习 3.9节 k-近邻学习)
