1. SVM简介
支持向量机(support vector machine SVM)是一种二类分类模型。它的基本模型是定义在特征空间(feature space)上的间隔最大线性分类器
因为SVM加入了间隔最大这项约束,所以SVM有别于别的感知机,即有唯一最优解(这一约束使其具备了结构化风险最小策略特性);除此之外支持向量机还包括核技巧,这使它成为实质上的非线性分类器。
支持向量机的模型是支持向量和超分类面的距离,学习策略就是间隔最大化,求解最优解的过程的算法根据待分类问题数据集的线性性决定是否需要用到kernel trick进行非线性求解,但总的来说,求解过程即求解凸二次规划(convex quadratic programming)问题,也等价于正则化的合页损失函数的最小化问题
支持向量机学习方法包含构建由简至繁的模型,简单模型是复杂模型的基础,也是复杂模型的特殊情况
1. 线性可分支持向量机(linear support vector machine in linearly separable case):当训练数据线性可分时,通过硬间隔最大化(hard margin maximization)学习一个线性的分类器,又称为硬间隔支持向量机 2. 线性支持向量机(linear support vector machine):当训练数据近似线性可分时(即存在部分噪音数据),通过软间隔最大化(soft margin maximization)学习一个线性的分类器,又称为软间隔支持向量机 3. 非线性支持向量机(non-linear support vector machine):当训练数据集完全线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机
0x1: 用一个故事简单概括SVM
我们用一个简单易懂的故事来引出我们今天的话题:
在很久以前的情人节,大侠要去救他的爱人,但魔鬼和他玩了一个游戏。魔鬼在桌子上似乎有规律放了两种颜色的球,说:“你用一根棍分开它们?要求:尽量在放更多球之后,仍然适用(仍然适用这个条件很重要,它暗示了对分类的要求约束)。”

于是大侠这样放,干的不错?这个过程就相当于感知机,只要找到一个可用的0-1分界面就可以了
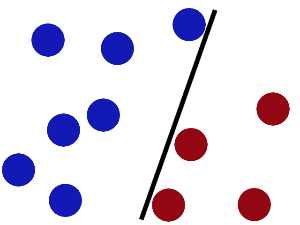
然后魔鬼,又在桌上放了更多的球,似乎有一个球站错了阵营。这也从侧面体现了感知机的泛化能力并不是那么强,通过分步梯度下降的"最优解"并不一定就是全局最优解
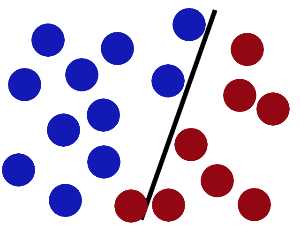
SVM就是试图把棍放在最佳位置(间隔最大化策略),好让在棍的两边有尽可能大的间隙。
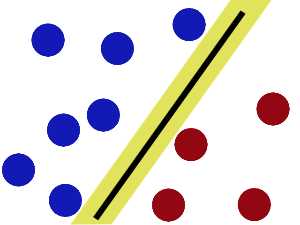
现在即使魔鬼放了更多的球,棍仍然是一个好的分界线(基于训练样本得到一个全局最好、泛化能力最强的分界面)。
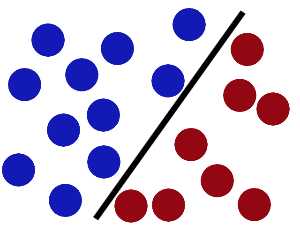
然后,在SVM 工具箱中有另一个更加重要的 trick(kernel trick)。 魔鬼看到大侠已经学会了一个trick,于是魔鬼给了大侠一个新的挑战。

现在,大侠没有棍可以很好帮他分开两种球了,现在怎么办呢?当然像所有武侠片中一样大侠桌子一拍,球飞到空中。然后,凭借大侠的轻功,大侠抓起一张纸,插到了两种球的中间。
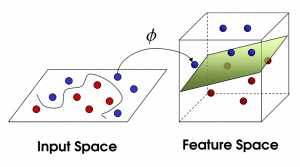
现在,从魔鬼的角度(二维)看这些球,这些球看起来像是被一条曲线分开了。
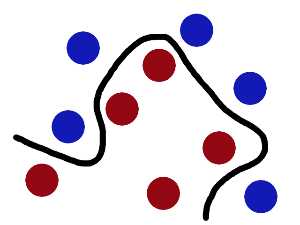
再之后,无聊的大人们,把这些球叫做 「data」,把棍子 叫做 「classifier」, 最大间隙trick 叫做「optimization」, 拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」。
0x2:用稍微数学一些分方法理解SVM
我们由简至深来认识SVM,让我们想象2个类别:红色和蓝色,我么的数据有2个维度的特征:x和y。我们想要一个分类器,给定一对(x, y)坐标,输出仅限于红色或蓝色
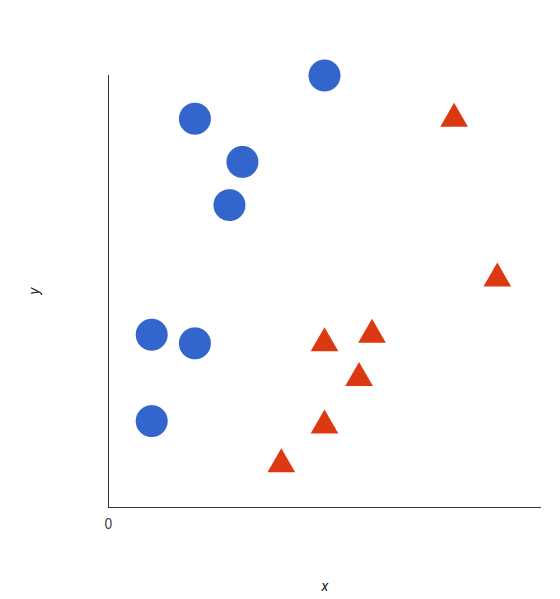
支持向量机会接受这些数据点,并输出一个超平面(在二维的图中,就是一条线)以将两类分割开来。这条线就是判定边界:将红色和蓝色分割开。
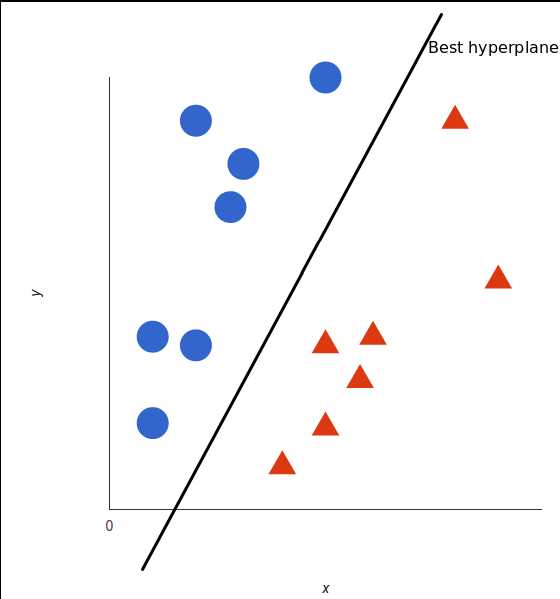
但是,最好的超平面是什么样的?对于 SVM 来说,它是最大化两个类别边距的那种方式,换句话说:超平面(在本例中是一条线)对每个类别最近的元素(这2个元素就叫支持向量)距离最远。
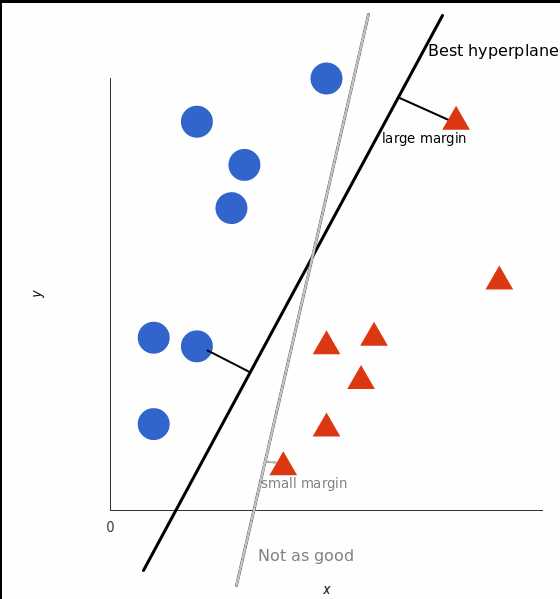
可以看到上图中黑色实现的分类面和灰色线的分类面的margin是不同的,SVM会计算出一个Max Margin的分类面
上面的例子很简单,因为那些数据是线性可分的——我们可以通过画一条直线来简单地分割红色和蓝色。然而,大多数情况下事情没有那么简单。看看下面的例子
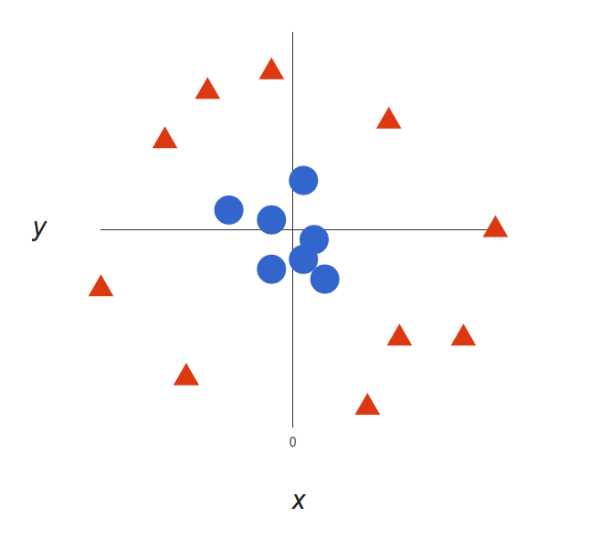
很明显,你无法找出一个(二元)线性决策边界(一条直线分开两个类别)。然而,两种向量的位置分得很开,看起来应该可以轻易地分开它们。 这个时候我们需要引入第三个维度。迄今为止,我们有两个维度:x 和 y。让我们加入维度 z,并且让它以直观的方式出现:z = x² + y²(圆形的方程式) 于是我们就有了一个三维空间,看看这个空间,它就像这样:
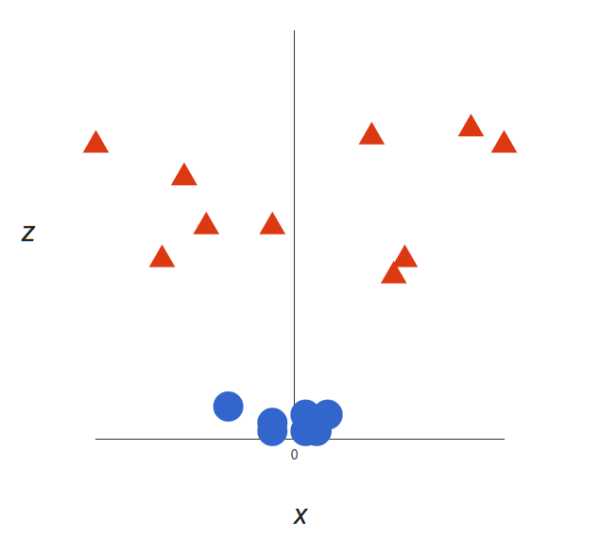
通过把数据集映射到3维空间,原本的"圆面面积"变成了"3维球体积",所有的数据点都在这个球体积中的某一个空间坐标位置
支持向量机将会如何区分它?很简单:
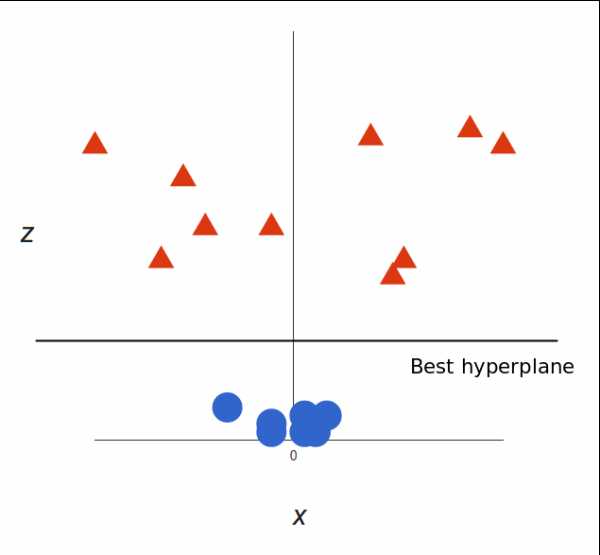
请注意,现在我们处于三维空间,超平面是 z 某个刻度上(比如 z=1)一个平行于 x 轴的平面。它在二维上的投影是这样:
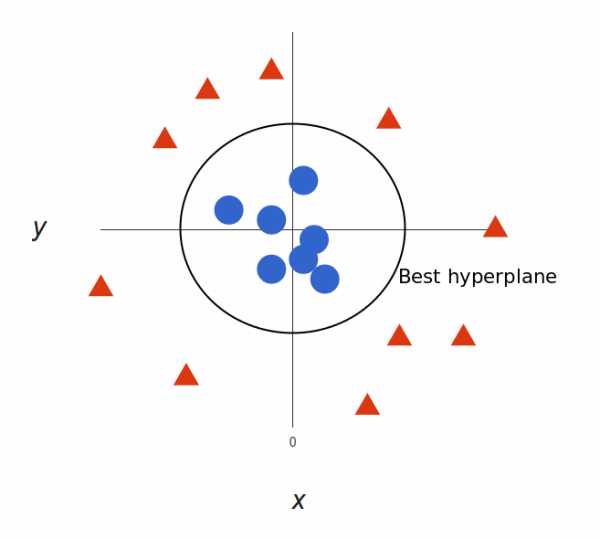
我们的决策边界就成了半径为 1 的圆形,通过 SVM 我们将其成功分成了两个类别
这里要思考一下问题了,这第三个维度是我们凭空想象出来的吗?异或是SVM自己虚构的一个新的维度?这么引入第三个维度是合理的吗?
我个人对Kernel Trick做维度提升的含义理解是这样的:
1. 首先,世界上基本不存在完全不可分的两类事物 2. 而所有的当前我们认为不可分的数据集,其实都是因为我们当前观察所在的维度太低,找不到那个区分点。事实上,区分点一直都在,只是隐藏在了当天的低维度中我们看不见 3. SVM要做的是找到一个合理的特征空间映射方式把那个原本隐藏的维度空间展示出来,在一个更高的新维度上,我们就可以用完全一样的普通分类技术去找到最佳分类面
0x3:对核函数的简单理解
当输入空间为欧氏空间或离散集合,特征空间为希尔伯特空间时,核函数(kernel function)表示将输入从输入空间映射到特征空间得到的特征向量之间的内积(内积的结果就是维度的扭曲提升)。通过核函数可以学习非线性支持向量机,等价于隐式地在高维的特征空间中学习线性支持向量机。这样的学习方法称为核技巧。核方法(kernel method)是比支持向量机更为一般的机器学习方法
为啥是映射到特征空间中特征向量的内积,这样的内积代表什么意思?特征空间为什么是高维的?
Relevant Link:
https://link.zhihu.com/?target=https%3A//v.qq.com/x/page/m05175nci67.html
2. 支持向量机算法模型
我们知道,支持向量机学习方法包含由简至繁的模型,所有模型中最基础的模型就是线性可分支持向量机(linear support vector machine in linearly separable case),其他的模型都是由此演进/改进得到的
0x1: 线性可分支持向量机
假设给定一个特征空间上的训练数据集: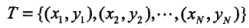 ,其中:
,其中: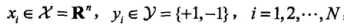 ,Xi为第i个特征向量,也称为实例,Yi为Xi的类标记,假设训练数据集是线性可分的
,Xi为第i个特征向量,也称为实例,Yi为Xi的类标记,假设训练数据集是线性可分的
学习的目标是在特征空间中找到一个分离超平面,能将实例分到不同的类,分离超平面对应于方程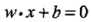 ,它由法向量w和截距b决定,可用(w,b)来表示。分离超平面将特征空间中的样本点划分为两部分,一部分是正类,一部分是负类。法向量指向的一侧为正类,另一侧为负类
,它由法向量w和截距b决定,可用(w,b)来表示。分离超平面将特征空间中的样本点划分为两部分,一部分是正类,一部分是负类。法向量指向的一侧为正类,另一侧为负类
一般地,当训练数据集线性可分时,存在无穷个分离超平面可将两类数据正确地分开。感知机利用误分类最小的策略求得分离超平面,但是这时的解有无穷多个(这是因为感知机模型对参数的约束要小的多,在一定的区间内允许误差不影响分类的结果)。线性可分支持向量机利用间隔最大化(结构化惩罚约束)求得最优分离超平面,这时解是唯一的(间隔最大化是一个强约束)
1. 线性可分支持向量机定义
给定线性可分训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为: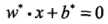 ,以及相应的分类决策函数:
,以及相应的分类决策函数: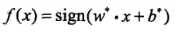 (根据结果的正负来决定预测的类别结果)称为线性可分支持向量机,线性可分支持向量机中包含了一个最大间隔的约束,要讨论最大间隔,我们需要先阐述间隔这个概念以及数学定义
(根据结果的正负来决定预测的类别结果)称为线性可分支持向量机,线性可分支持向量机中包含了一个最大间隔的约束,要讨论最大间隔,我们需要先阐述间隔这个概念以及数学定义
1)函数间隔
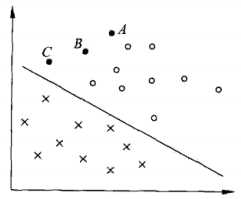
上图中,A,B,C表示3个实例,均在分离超平面的正类一侧。一般来说,一个点距离分离超平面的远近可以表示分类预测的确信程度(置信度连续值量化)。在超平面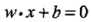 确定的情况下,
确定的情况下,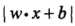 能相对地表示点 x 距离超平面的远近,而
能相对地表示点 x 距离超平面的远近,而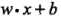 的符号与类标记 y 的符号是否一致能够表示分类是否正确
的符号与类标记 y 的符号是否一致能够表示分类是否正确
所以,用量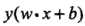 来表示分类的正确性以及确信度,这就是函数间隔(functional margin)的概念,它非常巧妙地把分类正确性已经置信度这两个概念融合到了一个数值化的数学公式中
来表示分类的正确性以及确信度,这就是函数间隔(functional margin)的概念,它非常巧妙地把分类正确性已经置信度这两个概念融合到了一个数值化的数学公式中
定义单个点的函数间隔:对于给定的训练数据集 T 和超平面(w,b),定义超平面(w,b)关于 T 中所有样本点(Xi,Yi)的函数间隔为: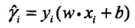
定义训练集的函数间隔:超平面(w,b)关于整个训练数据集 T 的函数间隔为超平面(w,b)关于 T 中所有样本点(Xi,Yi)的函数间隔最小值,即: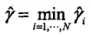 ,这个最小值本质上就是支持向量(support vector)和分离超平面的距离
,这个最小值本质上就是支持向量(support vector)和分离超平面的距离
2)几何间隔 - 规范化后的函数间隔,将量纲归一化到一个一致的量级中
函数间隔确实可以表示分类预测的正确性及确信度,但是很快就会发现选择分类超平面时,只有函数间隔还不够,因为只要成比例改变w和b(例如将它们改为2w和2b),超平面并没有改变,但函数间隔却成为原来的2倍。这提示我们需要进行规范化,对法向量w和截距b进行规范化(等比例缩放):
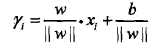 :点A在超平面的正侧
:点A在超平面的正侧
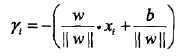 :点A在超平面的负一侧
:点A在超平面的负一侧
其中|| w ||为法向量w的L2范数。一般的,当样本点(Xi,Yi)被超平面(w,b)正确分类时,点Xi与超平面(w,b)的距离是: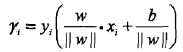 。这就是几何间隔的概念
。这就是几何间隔的概念
从函数间隔和几何间隔的定义可知,函数间隔和几何间隔有如下关系
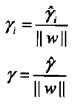 :几何间隔是归一化后的函数间隔
:几何间隔是归一化后的函数间隔
0x2:线性支持向量机
软间隔最大化
0x3:非线性支持向量机
基于kernel trick(核技巧)在新的特征空间中硬/软间隔最大化
Relevant Link:
李航《统计学习方法》7章
3. 支持向量机模型策略
模型策略是在模型定义的数学公式基础上施加的额外约束,在机器学习领域大多数时候是为了追求最优化估计,例如ML(最大似然估计)、EM估计、最后后验估计
0x1:间隔最大化(硬间隔最大化)
我们前面说过, SVM的策略是间隔最大化(线性和非线性情况下策略是不变的),我们前面已经确定了间隔的数学定义,接下来我们来讨论间隔最大化策略
支持向量机学习的基本法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。虽然线性可分分离超平面有无穷多个,但是几何间隔最大的分离超平面只有一个
间隔最大化的直观解释是:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练进行分类,不仅将正负实例分开,而且对最难分的实例点(离超平面最近的点)也有足够大的确信度将它们分开,这样的超平面“应该”对未知的新实例有很好的分类预测能力(泛化能力)
1. 最大间隔分离超平面
最大间隔分离超平面可以抽象为下面的约束最优化问题
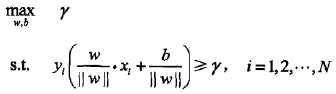 ,约束表明超平面(w,b)关于每个训练样本点的集合间隔都大于等于样本集和超平面的几何间隔(即样本集的支持向量的几何间隔是最短距离的那个)
,约束表明超平面(w,b)关于每个训练样本点的集合间隔都大于等于样本集和超平面的几何间隔(即样本集的支持向量的几何间隔是最短距离的那个)
将几何间隔改写为函数间隔: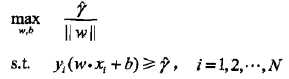 ,值得注意的是我们的求解对象是w,b,所以函数间隔本身的值大小并不影响最优化问题的解,这样,就可以取函数间隔
,值得注意的是我们的求解对象是w,b,所以函数间隔本身的值大小并不影响最优化问题的解,这样,就可以取函数间隔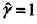 ,同时,最大化
,同时,最大化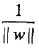 和最小化
和最小化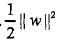 是等价的(对偶问题),所以上式可以改为写:
是等价的(对偶问题),所以上式可以改为写: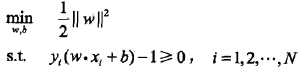 (Xi,Yi是训练实例点)。这是一个凸二次规划(convex quadratic programming)问题,即目标函数是二次函数且约束函数是仿射函数
(Xi,Yi是训练实例点)。这是一个凸二次规划(convex quadratic programming)问题,即目标函数是二次函数且约束函数是仿射函数
如果求出了上述约束最优化(有约束下的最优化)的解w,b。那么就可以得到最大间隔分离超平面以及分类决策函数
下面用一个例子来说明约束条件下求最大间隔模型的最优解
已知一个如下图所示的训练数据集,其正例点是X1 = (3,3),X2 = (4,3),负例点是X3 = (1,1)
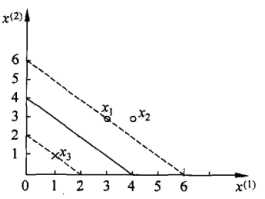
根据训练数据集构造约束最优化问题
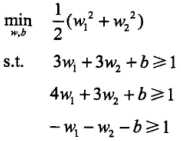
3个不等式求3个变元极有可能能得到最优解,从直观几何上可以理解为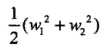 这个圆和3条切线的切点,显然可以使得
这个圆和3条切线的切点,显然可以使得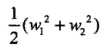 最小的切线是和(1,1)和(3,3)仿射线的所对应的约束,因此求得此最优化问题的解w1 = w2 = 1/2,b = -2。于是最大间隔分离超平面为:
最小的切线是和(1,1)和(3,3)仿射线的所对应的约束,因此求得此最优化问题的解w1 = w2 = 1/2,b = -2。于是最大间隔分离超平面为: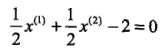 ,其中
,其中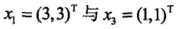 为支持向量
为支持向量
上述我们给出了硬间隔最大化的求解数学模型,那具体工程化时如何求解呢?难道是遍历所有样本点吗?显然那样效率太低了尤其在海量数据情况下无法实现,为了解决这个问题,就有了线性可分支持向量机的对偶算法(dual algorithm)和 “序列最小最优化算法”(参见第二章)
支持向量和间隔边界
在线性可分情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量(support vector)。支持向量可表示为: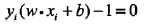
1. 对Yi = +1的正例点,支持向量在超平面 wx + b = 1 上 2. 对Yi = -1的负例点,支持向量在超平面wx + b = -1上
下图在H1和H2上的点就是支持向量
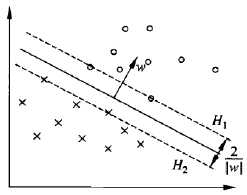
注意到H1和H2平行,并且没有任何实例点落在它们中间(约束条件要求支持支持向量必须是距离最短的点)。在H1和H2之间形成一条长带,分离超平面与它们平行且位于它们中央,长带的宽度称为间隔(marging),间隔依赖于分离超平面的法向量w,等于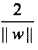 ,H1和H2称为间隔边界
,H1和H2称为间隔边界
在决定分离超平面时只有支持向量起作用,而其他实例点不起作用。由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称为支持向量机。支持向量机的个数一般很少,所以支持向量机由很少的“重要的”的训练样本确定
这里要注意的是,SVM虽然决定分界面的支持向量很少,但是参与训练计算的实例点并不少,甚至还很复杂,甚至从某种程度上来说,SVM的训练过程计算消耗是所有机器学习算法里最慢的
4. 线性可分支持向量机的对偶算法(dual algorithm)
我们已经知道SVM的模型是支持向量和分离超平面的集合距离(或者函数距离),SVM的策略是间隔最小化。但是这个间隔最小化是一个约束最优化问题,即
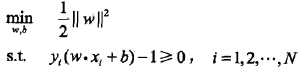 ,很显然,这个公式并不能通过简单的求导/逼近得到,为了解决这个问题,我们需要应用拉格朗日对偶性,通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解。这样做有2个好处
,很显然,这个公式并不能通过简单的求导/逼近得到,为了解决这个问题,我们需要应用拉格朗日对偶性,通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解。这样做有2个好处
1. 一是对偶问题更容易求解(更容易求导) 2. 自然引入核函数,进而推广到非线性分类问题
我们首先构建拉格朗日函数(lagrange function),对上式的每一个不等于约束引入拉格朗日乘子(lagrange multiplier)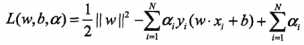 ,其中
,其中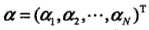 为拉格朗日乘子向量。根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
为拉格朗日乘子向量。根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题: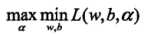 ,所以,为了得到对偶问题的解,需要先求L(w,b,a)对w,b的极小,再求a的极大
,所以,为了得到对偶问题的解,需要先求L(w,b,a)对w,b的极小,再求a的极大
(1)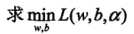
将拉格朗日函数L(w,b,a)分别对w,b求偏导数,并令其等于0。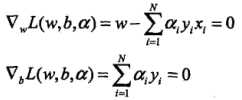 ,得
,得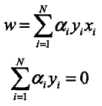 。带入上式拉格朗日函数,得
。带入上式拉格朗日函数,得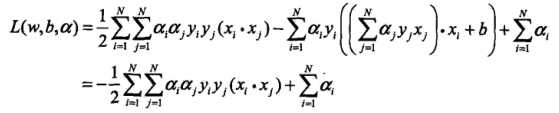
即: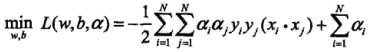
(2)求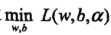 对a的极大,即是对偶问题:
对a的极大,即是对偶问题: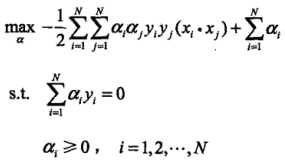 。将该目标函数由极大转换成求极小,得到等价的对偶最优化问题:
。将该目标函数由极大转换成求极小,得到等价的对偶最优化问题: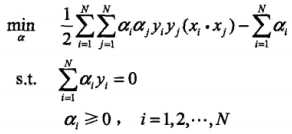
以上就是求解线性可分模型的对偶求解算法,用一个例子来更好地说明。已知一个如下图所示的训练数据集,其正例点是X1 = (3,3),X2 = (4,3),负例点是X3 = (1,1)

根据所给数据,对偶问题是: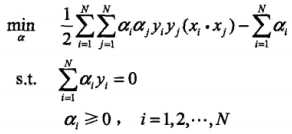
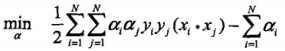 = 1 / 2 * ((3*3+3*3 * a1 * a1)+(4*4+3*3 * a2 * a2)+(1*1+1*1 * a3 * a3)+(3*4+3*3*2 * a1*a2)+(3*1+3*1*2 * a1*a3)+(4*1+3*1*2 * a2*a3)) - a1 - a2 - a3
= 1 / 2 * ((3*3+3*3 * a1 * a1)+(4*4+3*3 * a2 * a2)+(1*1+1*1 * a3 * a3)+(3*4+3*3*2 * a1*a2)+(3*1+3*1*2 * a1*a3)+(4*1+3*1*2 * a2*a3)) - a1 - a2 - a3
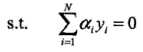 = a1 + a2 - a3 = 0
= a1 + a2 - a3 = 0
ai >= 0,i = 1,2,3
解这一最优化问题,将a3 = a1 + a2带入目标函数,得: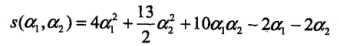
并对a1,a3求偏导数并令其为0,易得s(a1,a2)在点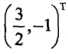 取得极值,但该点不满足约束条件:
取得极值,但该点不满足约束条件: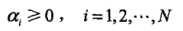 ,所以最小值应该在边界上达到。当a1 = 0时,最小值s(0,2/13) = - 2 /13;当a2 = 0时,最小值s(1/4,0) = - 1/4。所以s(a1,a2)在a1 = 1/4,a2 = 0达到最小,此时a3 = a1 + a2 = 1/4
,所以最小值应该在边界上达到。当a1 = 0时,最小值s(0,2/13) = - 2 /13;当a2 = 0时,最小值s(1/4,0) = - 1/4。所以s(a1,a2)在a1 = 1/4,a2 = 0达到最小,此时a3 = a1 + a2 = 1/4
所以,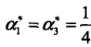 对应的实例点x1,x2是支持向量。根据
对应的实例点x1,x2是支持向量。根据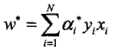 可得
可得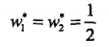 。又由
。又由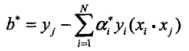 可得
可得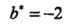
最终计算得分离超平面为: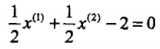 ,分类决策函数为:
,分类决策函数为: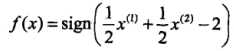
Relevant Link:
http://blog.csdn.net/xianlingmao/article/details/7919597 https://www.zhihu.com/question/38586401
4. 线性支持向量机与软间隔最大化
这小节我们继续讨论基于线性分类器的线性支持向量机的问题。我们上一节已经讨论了在数据集线性可分的情况下,使用线性支持向量机(硬间隔最大化)算法是最完美的,它能找到一个全局最优解,并且具有很好的泛化能力。但是在现实问题中,训练数据集往往是线性不可分的,但是这里的线性不可分也要分情况讨论
1. 训练数据集中存在一些噪音点,如果能去掉这些噪音点,训练集还是线性可分的 2. 训练数据集整个就完全线性不可分,再怎么去噪还是不可分,必须要用非线性分类器才能分开
我们由浅入深,先来讨论数据集中存在噪音点的情况,为了能将硬间隔最大化模型扩展到线性不可分(存在噪音点情况)的场景,我们需要修改硬间隔最大化模型,使其成为软间隔最大化
0x1: 带松弛变量的线性支持向量机
假设给定一个特征空间上的训练数据集: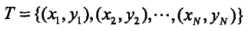 ,其中
,其中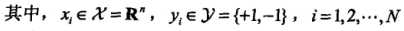 ,Xi为第i个特征向量,Yi为Xi的类标记。通常情况下,训练数据中有一些特异点(outlier),将这些特异点除去后,剩下大部分的样本点组成的集合是线性可分的
,Xi为第i个特征向量,Yi为Xi的类标记。通常情况下,训练数据中有一些特异点(outlier),将这些特异点除去后,剩下大部分的样本点组成的集合是线性可分的
线性不可分意味着某些样本点(Xi,Yi)不能满足函数间隔大于等于最小间隔点的约束条件(即支持向量的函数间隔是全数据集中最小的这一约束不成立了),为了解决这个问题,可以对每个样本点(Xi,Yi)引进一个松弛变量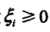 ,使那些特异点的函数间隔加上松弛变量大于等于1,这样,约束条件变为:
,使那些特异点的函数间隔加上松弛变量大于等于1,这样,约束条件变为: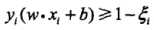 ,同时,对每个松弛变量
,同时,对每个松弛变量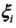 ,支付一个代价
,支付一个代价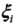 (类似于结构风险的思想),目标函数由原来的
(类似于结构风险的思想),目标函数由原来的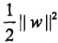 变成了:
变成了: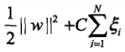 ,这里C > 0称为惩罚参数,一般由具体应用问题决定
,这里C > 0称为惩罚参数,一般由具体应用问题决定
1. C值大时对误分类的惩罚增大,即希望尽量少的容忍误分类 2. C值小时对误分类的惩罚减小
带松弛变量惩罚的最小化目标函数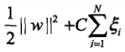 包含两层含义:(1)使
包含两层含义:(1)使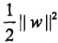 尽量小即间隔尽量大(这是基础线性支持向量机的策略);(2)同时使误分类点的个数在可能的情况下尽量小。C是动态调和二者的系数
尽量小即间隔尽量大(这是基础线性支持向量机的策略);(2)同时使误分类点的个数在可能的情况下尽量小。C是动态调和二者的系数
引入松弛变量后,可以和训练数据集线性可分时一样的方法来训练带噪点的线性不可分数据集。相对于硬间隔最大化,它称之为软间隔最大化
线性不可分的线性支持向量机的学习问题变成如下凸二次规划(convex quadratic programming)问题
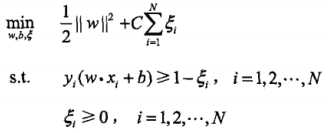
可以证明w的解是唯一的,但b的解不唯一,b的解存在于一个区间
0x2: 支持向量
在带噪点的线性不可分数据集情况下,这时的支持向量要比线性可分时的情况要复杂一些。图中,分离超平面由实线表示,间隔边界由虚线表示,实例Xi到间隔边界的距离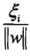 (每个特异点对应一个松弛变量)
(每个特异点对应一个松弛变量)
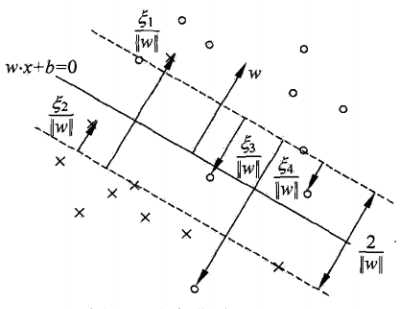
软间隔的支持向量Xi所在位置有3种可能的情况
(1)若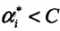 ,则
,则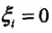 ,支持向量Xi恰好落在间隔边界上
,支持向量Xi恰好落在间隔边界上
(2)若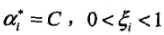 ,则分类正确,Xi在间隔边界与分类超平面之间
,则分类正确,Xi在间隔边界与分类超平面之间
(3)若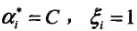 ,则Xi在分离超平面上
,则Xi在分离超平面上
(4)若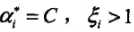 ,则Xi位于分离超平面误分一侧
,则Xi位于分离超平面误分一侧
5. 非线性支持向量机与核函数
对求解线性分类问题,线性分类支持向量机是一种非常有效的方法。但是,有时分类问题是非线性的,这是可以使用非线性支持向量机。本章节讨论的非线性支持向量机主要特点是利用核技巧(kernel trick),值得注意的是,核技巧不仅应用于支持向量机,而且应用于其他统计学习问题
0x1: 核技巧
博主个人觉得核技巧是SVM这一部分最难理解的理论了(至少对我来说),我们来逐步推理说明为什么要引入核函数,以及核函数到底发挥了什么作用
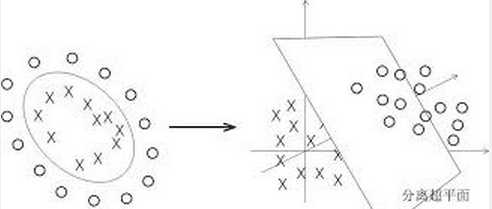
上图左边的原始样本输入空间是一个线性不可分的数据集,们可以将样本通过一个映射函数(具体函数公式我们还不知道,只知道映射后的维度比原始的要大)把它从原始空间投射到一个更高维的特征空间,使得样本在更高维的特征空间线性可分(如右图)。
我们暂时不讨论核函数的具体形式,我们假设我们已经得到了原始数据集在高维特征空间的表示。依旧采用最大间隔策略,我们对高维空间的特征向量建立约束条件
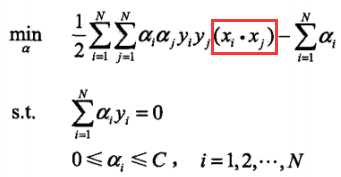
我们马上发现,我们面临的高维空间的内积运算,以及之后的对偶问题求解,这非常消耗计算资源,而且随着维度的继续增大,我们会遇到“维度灾难”问题。所以很自然的我们要想:我们需要一种数学技巧或者近似表示能够帮助我们简化计算
这时候就要引出核函数了,核函数决定了映射函数(给定一个核函数,映射函数并不唯一),我们选择了一个核函数(线性核、高斯核等等)就可以选择了一种映射方式(对于一个半正定核矩阵,总能找到一个与之对应的映射),这个映射函数实现了将低维特征空间映射到高维特征空间“等价转换”(这里是引号括起来是想表达这里的等价不是完全等价的,这只是一种数学上的近似等价)。
需要注意的是:
特征空间的好坏对支持向量机的性能至关重要。在不知道特征映射的形式时,我们并不知道什么样的核函数是合适的,而核函数也仅是隐式定义了这个特征空间。
于是,核函数的选择成为了支持向量机的最大变数。若核函数选择不合适,则意味着映射到一个不合适的特征空间,很可能导致性能不佳
在实际的工程项目中,我们往往需要根据我们的训练集去不断调整核函数,并观察模型的拟合和泛化能力
核函数的数学定义:
设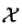 是输入空间(欧式空间
是输入空间(欧式空间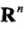 的子集或者离散集合),又设
的子集或者离散集合),又设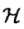 为特征空间(希尔伯特空间),如果存在一个从
为特征空间(希尔伯特空间),如果存在一个从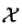 到
到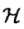 的映射:
的映射: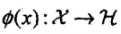 使得对所有
使得对所有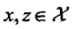 ,函数
,函数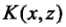 满足条件:
满足条件: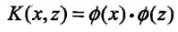 。则称
。则称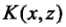 为核函数,
为核函数,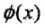 为映射函数
为映射函数
核技巧的思想是:在学习与预测中只定义核函数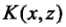 ,而不显式地定义映射函数
,而不显式地定义映射函数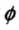 。通常,直接计算
。通常,直接计算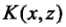 比较容易,而计算映射函数的内积并不容易。注意,
比较容易,而计算映射函数的内积并不容易。注意,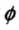 是输入空间
是输入空间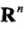 到特征空间
到特征空间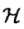 的映射,特征空间
的映射,特征空间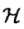 一般是高维的,甚至是无穷维的。可以看到,对于给定的核
一般是高维的,甚至是无穷维的。可以看到,对于给定的核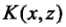 ,特征空间
,特征空间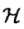 和映射函数
和映射函数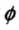 的取法并不唯一,可以取不同的特征空间,即使是在同一特征空间里也可以取不同的映射
的取法并不唯一,可以取不同的特征空间,即使是在同一特征空间里也可以取不同的映射
0x2: 核函数和映射函数关系举例
接下来我们用一个例子来说明核函数和映射函数的关系。假设输入空间是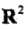 (二维空间),选定的核函数是
(二维空间),选定的核函数是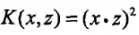 ,我们的目标是找出相关的特征空间
,我们的目标是找出相关的特征空间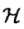 和映射
和映射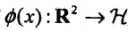
(1)记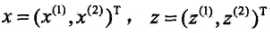 ,由于
,由于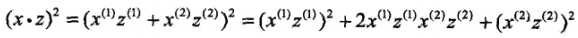 ,所以可以取映射
,所以可以取映射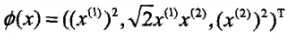 。容易验证
。容易验证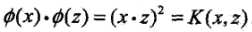 ,所以特征空间
,所以特征空间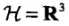 (三维空间)
(三维空间)
(2)我们前面说了,对于给定的核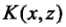 ,特征空间
,特征空间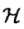 和映射函数
和映射函数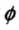 的取法并不唯一,可以取不同的特征空间,即使是在同一特征空间里也可以取不同的映射
的取法并不唯一,可以取不同的特征空间,即使是在同一特征空间里也可以取不同的映射
我们仍取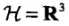 ,但这次换另一个映射函数:
,但这次换另一个映射函数: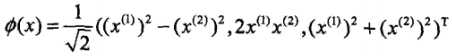 ,可以证明,同样有
,可以证明,同样有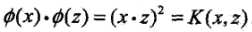
(3)甚至特征空间也不是一定的,我们还可以取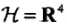 以及映射函数
以及映射函数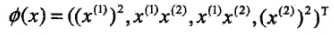
0x3: 核技巧在支持向量机中的应用
我们注意到在线性支持向量机的对偶求解中,无论是目标函数还是决策函数(分离超平面)都只涉及到输入实例与实例之间的内积。可以看到,在对偶问题的目标函数中的内积 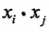 ,我们对这些内积进行映射函数变换后,可以用核函数
,我们对这些内积进行映射函数变换后,可以用核函数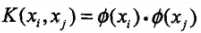 来代替,此时映射后的对偶问题的目标函数变为:
来代替,此时映射后的对偶问题的目标函数变为: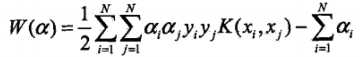 ,同样,分类决策函数中的映射函数变换后的内积也可以用核函数替代:
,同样,分类决策函数中的映射函数变换后的内积也可以用核函数替代: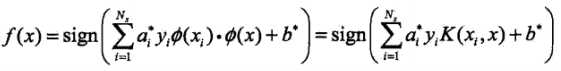
这等价于经过映射函数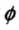 将原来的输入空间变换到了一个新的特征空间(维度更高),将输入空间中的内积
将原来的输入空间变换到了一个新的特征空间(维度更高),将输入空间中的内积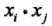 变换为新特征空间中的
变换为新特征空间中的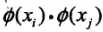 (等价变换),在新的特征空间里从训练样本中学习线性支持向量机
(等价变换),在新的特征空间里从训练样本中学习线性支持向量机
当映射函数是非线性函数时,学习到的含有核函数的支持向量机是非线性分类模型。也就是说,在核函数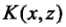 给定的条件下,可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在新特征空间里进行的,不需要显式地定义特征空间和映射函数,这样的技巧称为核技巧,它是巧妙地利用线性分类学习方法与核函数解决非线性问题的技术
给定的条件下,可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在新特征空间里进行的,不需要显式地定义特征空间和映射函数,这样的技巧称为核技巧,它是巧妙地利用线性分类学习方法与核函数解决非线性问题的技术
0x4: 常用核函数
1. 线性核(Linear Kernel) K(x,x′)=xx′K(x,x′)=xx′:

2. 多项式核(polynomial kernel function)
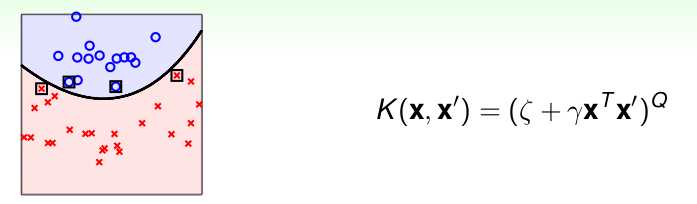
对应的支持向量机是一个Q次多项式分类器
3. 高斯核(gaussian kernel function)
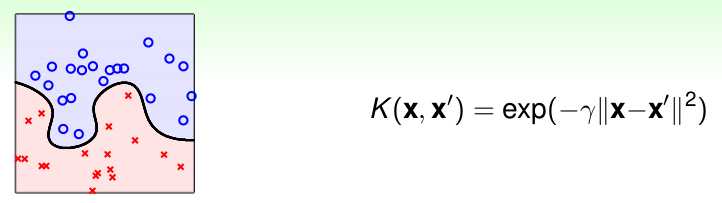
对应的支持向量机是高斯径向基函数(radial basis function)分类器
Relevant Link:
http://www.jianshu.com/p/446fae533b17
http://bytesizebio.net/2014/02/05/support-vector-machines-explained-well/
https://www.zhihu.com/question/21094489
https://www.reddit.com/r/MachineLearning/comments/15zrpp/please_explain_support_vector_machines_svm_like_i/
http://blog.csdn.net/u011067360/article/details/25503073
http://shomy.top/2017/02/19/svm03-kernel-trick/
https://wizardforcel.gitbooks.io/dm-algo-top10/content/svm-4.html
https://www.idaima.com/article/2725
https://www.zhihu.com/question/24627666
http://www.jianshu.com/p/ba59631855a3
6. SVM和感知机的区别
感知机和SVM都是二分类模型,但是它们之间在原理和策略思想上存在区别
1. 感知机根据误分类的样本点计算损失函数,相当于经验风险策略;而SVM不仅考虑从样本点计算经验风险,还引入了间隔最大约束,相当于结构化风险模型 2. 感知机是线性分类模型;SVM可以认为是以感知机为基础(它也有线性分类SVM),但是SVM可以通过核函数建立非线性分类模型;补充一句:逻辑斯蒂回归和深度神经网络本质上是利用了激活函数以及多层结构同样基于线性的感知机建立了非线性模型,它们和SVM的目的是一样的,只不过从另一个方向去实现该目的 3. 感知机采取梯度下降这类方式逐步逼近最优解(局部最优逼近全局最优);SVM通过拉格朗日对偶直接求解凸函数的全局最优解
0x1: 从一个数据集分类问题讨论开去 - 看感知机模型如何自然演进到SVM模型
我们前面说感知机模型是SVM的基础,我们接下来看一个例子
谈起分类,就不得不提一个经典分类概念:线性分类器
给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者-1,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper
plane),这个超平面的方程可以表示为(wT中的T代表转置),
假设函数就是特征属于y=1的概率

从而,当我们要判别一个新来的特征属于哪个类时,只需求 即可(它是一个决策函数),若
即可(它是一个决策函数),若 大于0.5就是y=1的类,反之属于y=0类。如果我们只从
大于0.5就是y=1的类,反之属于y=0类。如果我们只从 出发,希望模型达到的目标就是让训练数据中y=1的特征
出发,希望模型达到的目标就是让训练数据中y=1的特征 ,而是y=0的特征
,而是y=0的特征 。线性分类模型(感知机)就是要学习得到
。线性分类模型(感知机)就是要学习得到 ,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
如下图所示,现在有一个二维平面,平面上有两种不同的数据,分别用圈和叉表示。由于这些数据是线性可分的,所以可以用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所对应的y全是 -1 ,另一边所对应的y全是1
这个超平面可以用分类函数
确定了超平面之后,在进行分类的时候,遇到一个新的数据点x,将x代入f(x) 中,如果f(x)小于0则将x的类别赋为-1,如果f(x)大于0则将x的类别赋为1。接下来的问题是如何确定这个超平面?
这就是一个非常有趣的分界点了!!这是一个策略问题!!
1. 逻辑斯蒂回归和深度神经网络(多层逻辑斯蒂回归网络)选择的策略是误分类最小化策略,并使用梯度下降逐步逼近最优解的算法 2. SVM选择的策略是最大间隔距离最小化策略(最大间隔和最小化距离分别是2个约束公式),并使用拉格朗日乘子将这2个约束整合到一起,分别求偏导得到全局最优值
梯度下降我们不在本章讨论,我们来重点关注SVM的策略,还是回到上面找分离超平面的问题,从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定"最适合"的标准就是这条直线离直线两边的数据的间隔最大。所以,得寻找有着最大间隔的超平面(距离判定模型)
在超平面w*x+b=0确定的情况下,|w*x+b|能够表示点x到距离超平面的远近,而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了函数间隔(functional margin)的概念。定义函数间隔(用
而超平面(w,b)关于T中所有样本点(xi,yi)的函数间隔最小值(正值)(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
仔细看这个公式,它具备几个特点
1. 必须分类正确,才至少会是正值,如果那个样本点分类错了,结果就会是负值,将会降低总体的total function margin 2. 在分类正确的基础上,分类超平面和点离得越远,total function margin的值越大,且是正值
但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b)(等比缩放),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),所以只有函数间隔还远远不够。
事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔(geometrical margin)的概念。
假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x0 ,w 是垂直于超平面的一个向量,

根据平面几何知识,有

又由于 x0 是超平面上的点,满足 f(x0)=0 ,代入超平面的方程


随即让此式



为了得到


从上述函数间隔和几何间隔的定义可以看出:几何间隔就是函数间隔除以||w||,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离
定义出了模型,接下来要确定策略,即最小距离最大化策略
对一个数据集进行分类,当超平面离数据点的“间隔”越大(模型对新的样本点的判断容错度就越高,泛化能力就越好),分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半
通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得




 。回顾下几何间隔的定义
。回顾下几何间隔的定义




 ,这个目标函数便是在相应的约束条件
,这个目标函数便是在相应的约束条件
如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔




0x2: SVM和感知机对同一份数据集的分类效果对比
因为感知机本质上是线性分类器,感知机的策略是误分类损失最小化,所以我们这小节用一个线性可分数据集来对比线性支持向量集合线性分类器在分界线上的区别
# -*- coding:utf-8 -*- import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import SGDClassifier from sklearn.datasets.samples_generator import make_blobs from sklearn import linear_model if __name__ == "__main__": # we create 50 separable points X, Y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60) # fit the SVM model clf_svm = SGDClassifier(loss="hinge", alpha=0.01, n_iter=200, fit_intercept=True) clf_svm.fit(X, Y) # fit the Logistic Regression model clf_logreg = linear_model.LogisticRegression(C=1e5) # we create an instance of Neighbours Classifier and fit the data. clf_logreg.fit(X, Y) # plot the line, the points, and the nearest vectors to the plane xx = np.linspace(-1, 5, 10) yy = np.linspace(-1, 5, 10) X1, X2 = np.meshgrid(xx, yy) Z_SVM = np.empty(X1.shape) Z_LOG = np.empty(X1.shape) for (i, j), val in np.ndenumerate(X1): x1 = val x2 = X2[i, j] p_svm = clf_svm.decision_function([[x1, x2]]) p_log = clf_logreg.decision_function([[x1, x2]]) Z_SVM[i, j] = p_svm[0] Z_LOG[i, j] = p_log[0] # svm decision_function plt.contour(X1, X2, Z_SVM, [-1.0, 0.0, 1.0] , colors=‘blue‘, linestyles=[‘dashed‘, ‘solid‘, ‘dashed‘] ) plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired, edgecolor=‘black‘, s=20) # Logistic Regression model decision_function plt.contour(X1, X2, Z_LOG, [1.0], colors=‘orange‘, linestyles=‘solid‘) plt.axis(‘tight‘) plt.show()
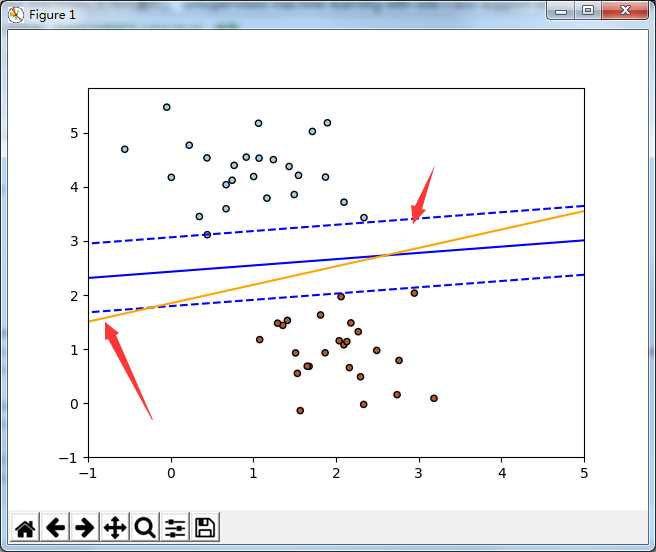
橙色的分解线是感知机(逻辑斯蒂回归分类)的分界线,蓝色的是SVM的分界线,可以看到,SVM的分界线泛化能力更好
Relevant Link:
http://blog.csdn.net/v_july_v/article/details/7624837 https://www.zhihu.com/question/51500780
7. Implementing and Visualizing SVM in Python with CVXOPT
svm-py-demo.py
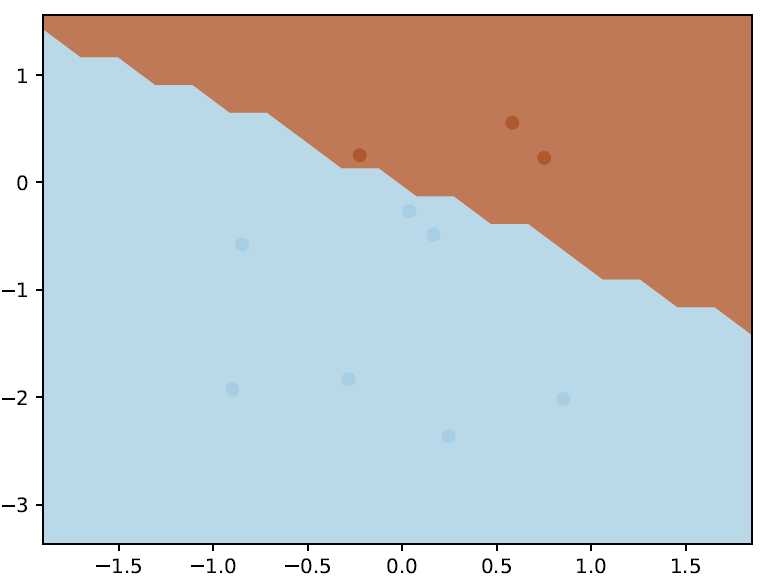
# -*- coding: utf-8 -*- #!/usr/bin/env python import svmpy import logging import numpy as np import matplotlib.pyplot as plt import matplotlib.cm as cm import itertools import argh def example(num_samples=10, num_features=2, grid_size=20, filename="svm.pdf"): # 随机产生一些num_features维度的向量 samples = np.matrix(np.random.normal(size=num_samples * num_features).reshape(num_samples, num_features)) print samples # 根据点所在空间位置是在坐标轴的上三角还是下三角进行label labels = 2 * (samples.sum(axis=1) > 0) - 1.0 print labels # 初始化一个线性核函数 trainer = svmpy.SVMTrainer(svmpy.Kernel.linear(), 0.1) # 根据输入样本得到一个SVM超平面分类面 predictor = trainer.train(samples, labels) # 根据已经得到的超平面对整个坐标系进行predict分类,并着色 plot(predictor, samples, labels, grid_size, filename) def plot(predictor, X, y, grid_size, filename): x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.linspace(x_min, x_max, grid_size), np.linspace(y_min, y_max, grid_size), indexing=‘ij‘) flatten = lambda m: np.array(m).reshape(-1,) result = [] for (i, j) in itertools.product(range(grid_size), range(grid_size)): point = np.array([xx[i, j], yy[i, j]]).reshape(1, 2) result.append(predictor.predict(point)) Z = np.array(result).reshape(xx.shape) plt.contourf(xx, yy, Z, cmap=cm.Paired, levels=[-0.001, 0.001], extend=‘both‘, alpha=0.8) plt.scatter(flatten(X[:, 0]), flatten(X[:, 1]), c=flatten(y), cmap=cm.Paired) plt.xlim(x_min, x_max) plt.ylim(y_min, y_max) plt.savefig(filename) if __name__ == "__main__": logging.basicConfig(level=logging.ERROR) argh.dispatch_command(example)
svm.py
import numpy as np import cvxopt.solvers import logging MIN_SUPPORT_VECTOR_MULTIPLIER = 1e-5 class SVMTrainer(object): def __init__(self, kernel, c): self._kernel = kernel self._c = c def train(self, X, y): """Given the training features X with labels y, returns a SVM predictor representing the trained SVM. """ lagrange_multipliers = self._compute_multipliers(X, y) return self._construct_predictor(X, y, lagrange_multipliers) def _gram_matrix(self, X): n_samples, n_features = X.shape K = np.zeros((n_samples, n_samples)) # TODO(tulloch) - vectorize for i, x_i in enumerate(X): for j, x_j in enumerate(X): K[i, j] = self._kernel(x_i, x_j) return K def _construct_predictor(self, X, y, lagrange_multipliers): support_vector_indices = lagrange_multipliers > MIN_SUPPORT_VECTOR_MULTIPLIER support_multipliers = lagrange_multipliers[support_vector_indices] support_vectors = X[support_vector_indices] support_vector_labels = y[support_vector_indices] # http://www.cs.cmu.edu/~guestrin/Class/10701-S07/Slides/kernels.pdf # bias = y_k - \sum z_i y_i K(x_k, x_i) # Thus we can just predict an example with bias of zero, and # compute error. bias = np.mean( [y_k - SVMPredictor( kernel=self._kernel, bias=0.0, weights=support_multipliers, support_vectors=support_vectors, support_vector_labels=support_vector_labels).predict(x_k) for (y_k, x_k) in zip(support_vector_labels, support_vectors)]) return SVMPredictor( kernel=self._kernel, bias=bias, weights=support_multipliers, support_vectors=support_vectors, support_vector_labels=support_vector_labels) def _compute_multipliers(self, X, y): n_samples, n_features = X.shape K = self._gram_matrix(X) print K # Solves # min 1/2 x^T P x + q^T x # s.t. # Gx \coneleq h # Ax = b P = cvxopt.matrix(np.outer(y, y) * K) q = cvxopt.matrix(-1 * np.ones(n_samples)) # -a_i \leq 0 # TODO(tulloch) - modify G, h so that we have a soft-margin classifier G_std = cvxopt.matrix(np.diag(np.ones(n_samples) * -1)) h_std = cvxopt.matrix(np.zeros(n_samples)) # a_i \leq c G_slack = cvxopt.matrix(np.diag(np.ones(n_samples))) h_slack = cvxopt.matrix(np.ones(n_samples) * self._c) G = cvxopt.matrix(np.vstack((G_std, G_slack))) h = cvxopt.matrix(np.vstack((h_std, h_slack))) A = cvxopt.matrix(y, (1, n_samples)) b = cvxopt.matrix(0.0) solution = cvxopt.solvers.qp(P, q, G, h, A, b) # Lagrange multipliers return np.ravel(solution[‘x‘]) class SVMPredictor(object): def __init__(self, kernel, bias, weights, support_vectors, support_vector_labels): self._kernel = kernel self._bias = bias self._weights = weights self._support_vectors = support_vectors self._support_vector_labels = support_vector_labels assert len(support_vectors) == len(support_vector_labels) assert len(weights) == len(support_vector_labels) logging.info("Bias: %s", self._bias) logging.info("Weights: %s", self._weights) logging.info("Support vectors: %s", self._support_vectors) logging.info("Support vector labels: %s", self._support_vector_labels) def predict(self, x): """ Computes the SVM prediction on the given features x. """ result = self._bias for z_i, x_i, y_i in zip(self._weights, self._support_vectors, self._support_vector_labels): result += z_i * y_i * self._kernel(x_i, x) return np.sign(result).item()
kernel.py
import numpy as np import numpy.linalg as la class Kernel(object): """Implements list of kernels from http://en.wikipedia.org/wiki/Support_vector_machine """ @staticmethod def linear(): return lambda x, y: np.inner(x, y) @staticmethod def gaussian(sigma): return lambda x, y: np.exp(-np.sqrt(la.norm(x-y) ** 2 / (2 * sigma ** 2))) @staticmethod def _polykernel(dimension, offset): return lambda x, y: (offset + np.inner(x, y)) ** dimension @classmethod def inhomogenous_polynomial(cls, dimension): return cls._polykernel(dimension=dimension, offset=1.0) @classmethod def homogenous_polynomial(cls, dimension): return cls._polykernel(dimension=dimension, offset=0.0) @staticmethod def hyperbolic_tangent(kappa, c): return lambda x, y: np.tanh(kappa * np.dot(x, y) + c) @staticmethod def radial_basis(gamma=10): return lambda x, y: np.exp(-gamma*la.norm(np.subtract(x, y)))
Relevant Link:
http://machinelearningmastery.com/understand-machine-learning-algorithms-by-implementing-them-from-scratch/ https://github.com/eriklindernoren/ML-From-Scratch/tree/master/mlfromscratch/unsupervised_learning https://github.com/ajtulloch/svmpy/blob/master/bin/svm-py-demo https://github.com/ajtulloch/svmpy https://github.com/goelhardik/svm-cvxopt http://goelhardik.github.io/2016/11/28/svm-cvxopt/ https://vimsky.com/article/222.html http://dataunion.org/4816.html
Copyright (c) 2016 LittleHann All rights reserved






