(本文是根据 neuralnetworksanddeeplearning 这本书的第三章Improving the way neural networks learn整理而成的读书笔记,根据个人口味做了删减)
上一章,我们介绍了神经网络容易出现的过拟合问题,并学习了最常用的正则化方法,以及其他一些技巧,今天,我们将介绍本章节最后两个问题:权重初始化和超参数的选择
权重初始化
到目前为止,我们都是用归一化高斯分布来初始化权值,但是,我们很想知道是否有其他初始化方法可以让网络训练得更好。
事实上,确实存在比高斯分布更好的方法。不过,我们需要先了解高斯分布的初始化会存在哪些缺陷。
假设我们有如下的网络结构,其中包含 1000 个输入神经元:
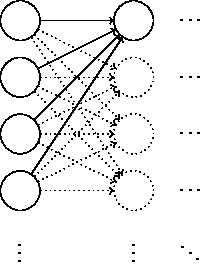
现在,我们聚焦于隐藏层第一个神经元。假设输入中,有一半的神经元是 0,一半的神经元是 1。输入到隐藏层的权重和为 \(z=\sum_j{w_j x_j}+b\)。由于有一半的 \(x_j=0\),所以 \(z\) 相当于是 501 个归一化的高斯分布随机变量的和。因此,\(z\) 本身也是一个高斯分布,其均值为 0,标准差为 \(\sqrt{501} \approx 22.4\)。这是一个很「宽」的分布:
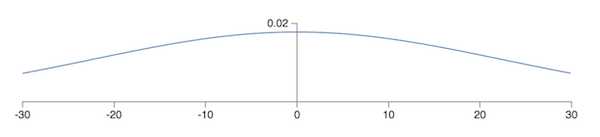
也就是说,大部分情况下 \(z \gg 1\) 或者 \(z \ll 1\)。对于采用 sigmoid 函数的 \(\sigma(z)\) 来说,这就意味着隐藏层可能已经收敛了(所谓收敛,就是训练开始变缓或停止了,而导致收敛的原因在于,偏导中的 \(\sigma‘(z)\) 在 \(|z|>1\) 时趋于 0,这样梯度下降就没法更新参数了)。之前我们用交叉熵函数解决了输出层中学习率低的问题,但对于中间的隐藏层并没有作用。而且,前一层隐藏层的输出如果也成高斯分布,那么再往后的隐藏层也会收敛。
改善这种问题的措施也很简单,既然问题根源在于高斯分布太「宽」,那么我们就想办法让它变「窄」,也就是标准差要变小。假设一个神经元有 \(n_{in}\) 个输入权值,那么我们只需要将所有权值按照均值为 0,标准差为 \(1/\sqrt{n_{in}}\) 的高斯分布初始化即可。这样得到的新的高斯分布就会「瘦高」得多。对于之前的例子,在 500 个输入为 0,500 个为 1 的情况下,新高斯分布的均值为 0,标准差为 \(\sqrt{3/2}=1.22…\),如下图所示:
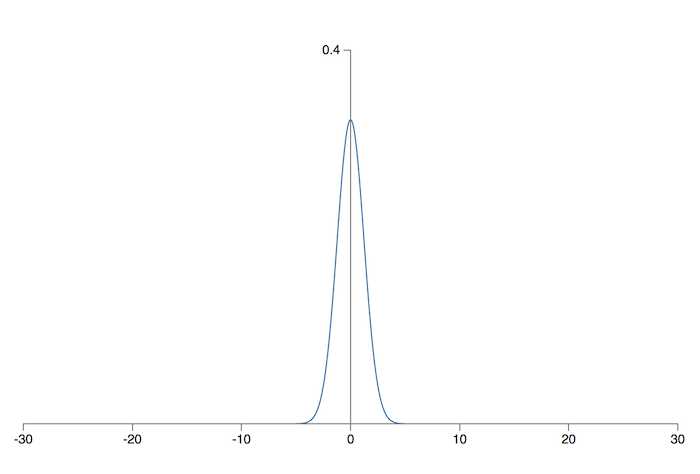
这样一来,\(z\) 的值普遍在 \([0, 1]\) 内,隐藏层过早收敛的情况也就有所缓解了。
我们再通过一组实验来看看不同初始化方法的效果:
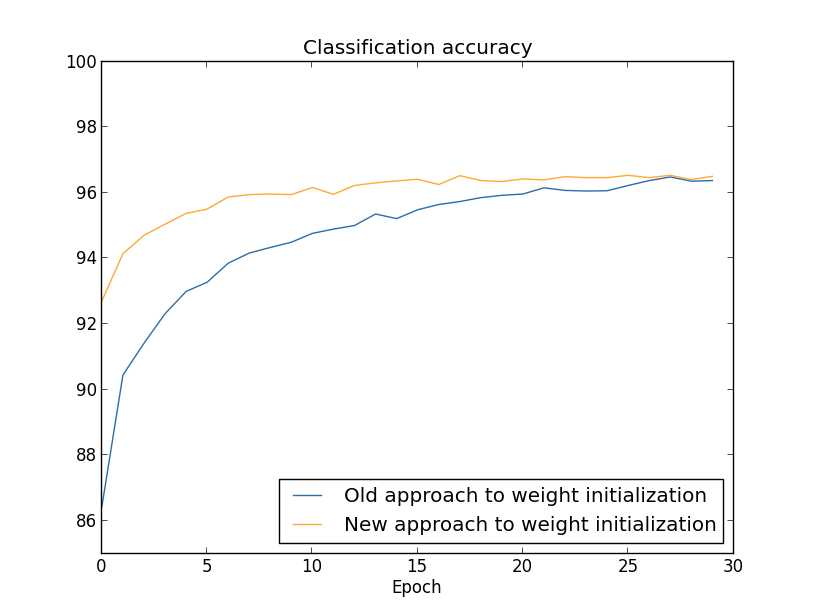
其中,橙线是用上面提及的新的高斯分布初始化,而蓝线则是一般的高斯分布。从结果来看,新的初始化方法可以加速网络的训练,但最终的准确率两者相当。不过在某些情况下,\(1/\sqrt{n_{in}}\) 的初始化方式会提高准确率,在下一章中,我们将看到类似的例子。
要注意的一点是,以上的初始化都是针对权值 weight 的,对偏差 bias 的初始化不影响网络的训练(原因暂时没想明白)。
如何选择超参数
到目前为止,我们都没有仔细讨论超参数该如何选择(如学习率 \(\eta\),正则化参数 \(\lambda\) 等等)。超参数的选择对网络的训练和性能都会产生影响。由于神经网络的复杂性,一旦网络出现问题,我们将很难定位问题的根源,搞不清楚到底是网络结构有问题,还是数据集有问题,还是超参数本身没选好。因此,这一节我们将学习一些选择超参数的「灵感」或者「准则」,减少在超参数选择上的失误。
宽泛的策略
之所以称之为宽泛,是因为这种策略不告诉如何调整超参数,而是让你尽可能快地得到反馈。只有尽快把握网络的学习情况,我们才有耐心和信息继续 debug(总不能每调整一次要等个十来分钟才出结果吧)。我自己在 debug 网络的时候也经常采用这些做法,比如,只用很小的数据集训练,或者将网络的结构变小等等。这些做法只有一个目的:让网络尽可能快地反馈结果,不管结果好坏,这是我们能继续调试下去的前提。在反复调试后,我们往往能得到一些「灵感」,之后再慢慢将问题变的更复杂一些,然后继续调试。
好了,下面我们针对学习率 \(\eta\)、L2 正则化参数 \(\lambda\) 和批训练的数据集大小学习一些比较有效的准则。
学习率
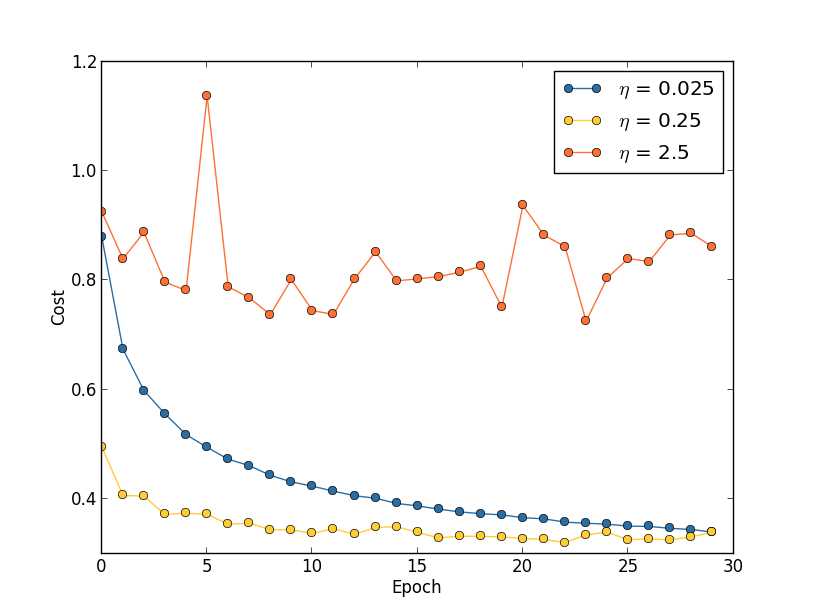
关于学习率的选择,Andrew Ng 在他的 Machine Learning 课程中有过详细的讲解。这里面最重要的是要避免学习率过大给梯度下降带来「抖动」的问题,如下图中的橙线所示。在设置学习率时,我们可以先设置一个小一点的数值,如 0.1,如果这个数值太大,则调低一个数量级到 0.01,甚至 0.001...如果发现学习过程中代价函数没有出现「抖动」的情况,再适当提高学习率,如由原来的 0.1 提高到 0.2、0.5...但最终不能超过造成「抖动」的阈值。
early stopping 选择训练轮数
在神经网络中,并不是训练得越多越好,之前已经提到过,训练太多轮可能导致过拟合。因此,我们要采取尽可能合适的训练轮数。early stopping 的具体做法是:在每一轮训练后观察验证集上的准确率,当验证集准确率不再上升时,就停止训练。这里的准确率不再上升指的是,在连续几轮(比如 10 轮)的训练后,准确率都不再有新的突破,始终维持在一个稳定的数值。
调整学习率
前面说过,学习率过大可能导致梯度下降出现「抖动」,过小又会导致网络训练太慢。在实际过程中,我们常常会遇到这样的问题:当网络开始训练时,由于 weights 不够好,这个时候加大学习率可以快速改善网络;当网络训练一段时间后,梯度下降开始到达最低点,这个时候小一点的学习率可以防治其越过最低点而出现「抖动」。因此,在训练过程中,更好的方法不是固定一个学习率,而是根据验证集上的准确率情况,逐步调整学习率(比如一开始设为 0.1,当准确率上升到 80% 后,调低到 0.01,上升到 90% 后,再继续调低,直到学习率只有初始值的千分之一为止)。
正则化参数
刚开始训练时,最好将正则化参数 \(\lambda\) 设为 0.0,等学习率确定并且网络可以正常训练后,再设置 \(\lambda\)。具体该设置为什么,没有通用的准则,只能根据实际情况判断,可以是 1.0,或者 0.1,或者 10.0。总之,要根据验证集上的准确率来判断。
批训练的数据集大小
理论上,我们完全可以在每次训练时只用一个样本,但这样会导致训练过程相当漫长,而多个样本进行批训练,在当今计算机的快速矩阵运算下并不比单个样本慢,这样相当于同时训练多个样本的时间和单个样本一样(当然,将所有样本都用于训练还是会影响速度,所以才会采用随机梯度训练的批样本)。另外,个人认为,综合多个样本再取均值进行训练,可以抵消部分噪音样本的影响。
