决策树之ID3算法
Content
1.ID3概念
2.信息熵
3.信息增益 Information Gain
4. ID3 bias
5. Python算法实现(待定)
一、ID3概念
ID3算法最早是由罗斯昆(J. Ross Quinlan)于1975年在悉尼大学提出的一种分类预测算法,算法的核心是“信息熵”。ID3算法通过计算每个属性的信息增益,认为信息增益高的是好属性,每次划分选取信息增益最高的属性为划分标准,重复这个过程,直至生成一个能完美分类训练样例的决策树。
决策树是对数据进行分类,以此达到预测的目的。该决策树方法先根据训练集数据形成决策树,如果该树不能对所有对象给出正确的分类,那么选择一些例外加入到训练集数据中,重复该过程一直到形成正确的决策集。决策树代表着决策集的树形结构。
ID3算法是一种贪心算法,用来构造决策树。ID3算法起源于概念学习系统(CLS),以信息熵的下降速度为选取测试属性的标准,即在每个节点选取还尚未被用来划分的具有最高信息增益的属性作为划分标准,然后继续这个过程,直到生成的决策树能完美分类训练样例。
首选分类方法:降低随机性——to a low entropy
红归红,绿归绿
回到classification 的本质,把混合的东西分开!
属于:增大信息增益——每次差异越大越好P.S.贪心算法:
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
奥卡姆剃刀原理:如无必要,勿增实体
ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,
即Iterative Dichotomiser 3,迭代二叉树3代,是Ross Quinlan发明的一种决策树算法,这个
算法的基础就是上面提到的奥卡姆剃刀原理,越是小型的决策树越优于大的决策树,尽管如此,也不总
是生成最小的树型结构,而是一个启发式算法。
在信息论中,期望信息越小,那么信息增益就越大,从而纯度就越高。ID3算法的核心思想就是以信息
增益来度量属性的选择,选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍
历可能的决策空间。
二、信息熵 Entropy
熵Entropy——测量随机性的一种方法
熵这个概念最早起源于物理学,在物理学中是用来度量一个热力学系统的无序程度,而在信息学里面,熵
是对不确定性的度量。在1948年,香农引入了信息熵,将其定义为离散随机事件出现的概率,一个系统越
是有序,信息熵就越低,反之一个系统越是混乱,它的信息熵就越高。所以信息熵可以被认为是系统有序
化程度的一个度量。
\[H(x) = - \sum_{i=1}^{n} P_{i} log_{2} P_{i} \]
三、信息增益 Information Gain
信息增益是针对一个一个特征而言的,就是看一个特征,系统有它和没有它时的信息量各是多少,两者
的差值就是这个特征给系统带来的信息量,即信息增益。
接下来以天气预报的例子来说明。下面是描述天气数据表,学习目标是play或者not play。
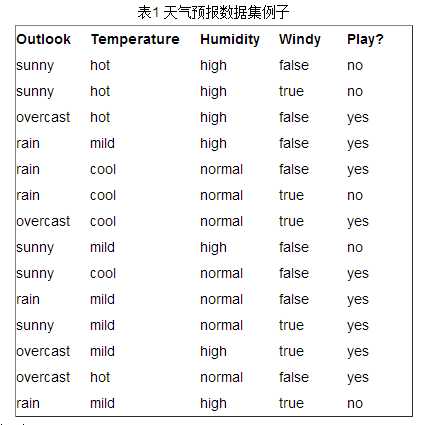
可以看出,一共14个样例,包括9个正例和5个负例。那么当前信息的熵计算如下
\[ Entropy(S) = -\frac{9}{14} log_2 \frac{9}{14} - \frac{5}{14} log_2 \frac{5}{14} = 0.940286\]
在决策树分类问题中,信息增益就是决策树在进行属性选择划分前和划分后信息的差值。假设利用
属性Outlook来分类,那么如下图
photo :outlook classification
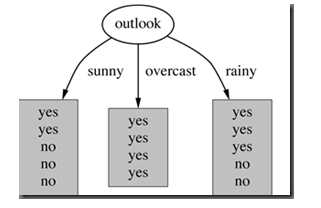
划分后,数据被分为三部分了,那么各个分支的信息熵计算如下
\[ Entropy(sunny) = -\frac{2}{5} log_2 \frac{2}{5} - \frac{3}{5} log_2 \frac{3}{5} = 0.970951\]
\[ Entropy(overcast) = 0\]
\[ Entropy(rainy) = -\frac{3}{5} log_2 \frac{3}{5} - \frac{2}{5} log_2 \frac{2}{5} = 0.970951\]
那么划分后的信息熵为
\[ Entropy(S|T) = \frac{5}{14}Entropy(sunny) +\frac{4}{14}Entropy(overcast)+\frac{5}{14}Entropy(rainy) = 0.693536 \]
Entropy(S|T)代表在特征属性T的条件下样本的条件熵。那么最终得到特征属性T带来的信息增益为
$$ IG(T) = Entropy(S) - Entropy(S|T) = 0.24675
信息增益计算公式:
\[ IG(S|T) = Entropy(S) - \sum_{value(T)} \frac{|S_v|}{S} Entropy(S_v) \]
其中为S全部样本集合,value(T)是属性T所有取值的集合,v是的T其中一个属性值,\(S_v\)是S中属性T的
值为v的样例集合,\(|S_v|\) 为\(S_v\)中所含样例数。
在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划
分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略。以上
就是ID3算法的核心思想。
四、 ID3 bias
review:搜索空间算法偏差
1.restriction bias 限定偏差
限定在假设集 hypothesis set
2.preference bias 优选偏差
告知首选的假设集中的假说的来源
- ID3 bias —— Inductive bias 归纳偏差
1.good splits near the top
2.correct over incorrect (偏向于正确的决策树而不是错误的决策树)
如果一个决策树在顶部有非常好的分割,但是生成了错误答案,它也不会选择。
P.S.看起来很愚蠢,but这就是工程思维。必须可量化,可执行。让机器可执行。
3.shorter trees(由第一条自然造成的结果)
参考:
http://blog.csdn.net/acdreamers/article/details/44661149
感悟:学习通信原理及信息论对 机器学习算法帮助很大
