问题描述:
输入是由一个随机过程产生的[0, 1)区间上均匀分布的实数。将区间[0, 1)划分为n个大小相等的子区间(桶),每桶大小1/n:[0, 1/n), [1/n, 2/n), [2/n, 3/n),…,[k/n, (k+1)/n ),…将n个输入元素分配到这些桶中,对桶中元素进行排序,注意,这里对每个桶中的元素进行排序其实可以选择很多算法,《算法导论》上是用了插入排序。
我在很多地方都看到有关这个问题的描述,发现很多人写的代码并不是《算法导论》上的桶排序,而是基数排序,两者的过程并不一样,虽然有部分过程类似。
桶排序要求输入数组中的数据是均匀分布在 [0, 1)上的,于是我用随机数产生了一系列[0, 1)之间的数。
即使输入数据不服从均匀分布,桶排序也仍然可以在线性时间内完成,只要输入数据满足下列性质:所有桶的大小的平方和总的元素数呈线性关系,
那么桶排序的时间复杂度就依旧是 Θ(n)。
下面的插入排序部分是基于之前插入排序写的。
-------------------------------------------代码------------------------------------------------
1 // 桶排序.cpp: 定义控制台应用程序的入口点。 2 // 3 4 #include "stdafx.h" 5 #include <iostream> 6 #include <vector> 7 #include <cstdlib> 8 #include <ctime> 9 10 using namespace std; 11 12 #define N 999 //三位小数。 13 14 int insertion_sort(vector<double> &A)//按升序排列 15 { 16 double key = 0; 17 int j = 0; 18 for (int i = 0; i < A.size(); i++)//依次取出原数组中的数 19 { 20 key = A[i]; 21 j = i - 1; 22 while (j >= 0 && A[j] > key)//如果按降序排列则改成j >= 0 && a[j] < key 23 { 24 A[j + 1] = A[j]; 25 j--; 26 } 27 A[j + 1] = key; 28 } 29 return 0; 30 } 31 32 int BUCKET_SORT(vector<double> &A)//数组A中的数据均匀地分布在[0,1)的范围中,那么我们把这个范围分成 10 段,对应10个桶 33 { 34 vector<vector<double>> bucket(10);//模拟二维数组,用指针数组也行 35 int temp; 36 for (int i = 0; i < A.size(); i++) 37 { 38 temp = (int)(A[i] * 10); 39 bucket[temp].push_back(A[i]); 40 } 41 42 for (int i = 0; i < 10; i++)//对每个桶进行插入排序 43 { 44 insertion_sort(bucket[i]); 45 } 46 47 int ptr = 0; 48 for (int i = 0; i < 10; i++) 49 for (int j = 0; j < bucket[i].size(); j++) 50 A[ptr++] = bucket[i][j]; 51 return 0; 52 } 53 54 int main() 55 { 56 vector<double> A; 57 double temp; 58 srand(time(NULL));//设置随机数种子,使每次获取的随机序列不同。 59 60 for (int i = 0; i < 10; i++) 61 { 62 temp = rand() % (N + 1) / (float)(N + 1);//生成0-1间的随机数。 63 A.push_back(temp); 64 } 65 for (auto c : A) 66 cout << c << ends; 67 cout << endl; 68 69 BUCKET_SORT(A); 70 for (auto c : A) 71 cout << c << ends; 72 cout << endl; 73 74 return 0; 75 }
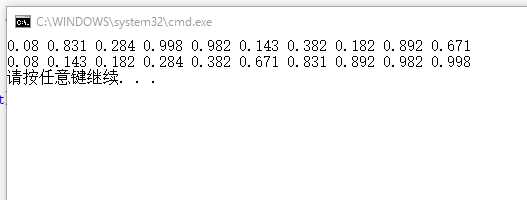
运行结果如下: