一、直线扫描算法:通过已知两点可以求得直线方程:
y = kx + b;
k = (y1-y0)/(x1-x0);
b = y0 - kx0;
1、数值微分法(DDA)
已知过端点P0 (x0, y0), P1(x1, y1)的直线段L:y = kx + b,容易得知直线斜率为:k = (y1-y0)/(x1-x0),(假设x1≠x0)。
我们假设|k|≤1,这样x每增加1,y将增加k,并且保证x每增加1,y的增量不能大于1;如果|k| > 1,则应该将x和y互换。由于k是浮点数,因此算法中需要将y舍入为int型,并圆整到最接近的位置。
DDA算法在每次迭代中的x, y值是上一步的值加上一个增量获得的,因此它是一个增量算法。但是这种方法直观,但效率太低,因为每一步需要一次浮点乘法和一次舍入运算。
2、中点画线法
在直线斜率在0~1直接的情况下,设当前像素点为(x,y),那么它的下一个像素点就是p1(x+1,y)或者p2(x+1,y+1),若称p1和p2的中点M(px+1,y+0.5),Q为理想直线与x+1垂线的交点,当Q在M的下方时,p1即为下一个像素点,否则p2即为下一个像素点。
3、Bresenham算法
过各行各列象素中心构造一组虚拟网格线。按直线从起点到终点的顺序计算直线与各垂直网格线的交点,然后确定该列象素中与此交点最近的象素。该算法的巧妙之处在于采用增量计算,使得对于每一列,只要检查一个误差项的符号,就可以确定该列的所求象素。
原理:

步骤:

二、区域填充算法
1、递归算法
从指定的种子点开始,向各个方向上搜索,逐个像素进行处理,直到遇到边界,各种种子填充算法只是在处理颜色和边界的方式上有所不同。
2、扫描线算法
扫描线种子填充算法的基本过程如下:当给定种子点(x, y)时,首先分别向左和向右两个方向填充种子点所在扫描线上的位于给定区域的一个区段,同时记下这个区段的范围[xLeft, xRight],然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段,并依次保存下来。反复这个过程,直到填充结束。
扫描线种子填充算法可由下列四个步骤实现:
(1) 初始化一个空的栈用于存放种子点,将种子点(x, y)入栈;
(2) 判断栈是否为空,如果栈为空则结束算法,否则取出栈顶元素作为当前扫描线的种子点(x, y),y是当前的扫描线;
(3) 从种子点(x,y)出发,沿当前扫描线向左、右两个方向填充,直到边界。分别标记区段的左、右端点坐标为xLeft和xRight;
(4) 分别检查与当前扫描线相邻的y - 1和y + 1两条扫描线在区间[xLeft,xRight]中的像素,从xLeft开始向xRight方向搜索,若存在非边界且未填充的像素点,则找出这些相邻的像素点中最右边的一个,并将其作为种子点压入栈中,然后返回第(2)步;
三、圆生成算法:通过给定圆中心点击圆半径绘制圆。
1.通过圆的定义:(x - Xc)^2 + (y - Yc)^2 = r^2;

2.假设圆的方程为:x2+y2=r2,则有函数:F(x,y)=x2+y2-r2
当F(x,y)>0时,对应的点(x,y)在圆外;
当F(x,y)<0时,对应的点(x,y)在圆外;
当F(x,y)=0时,对应的点(x,y)在圆上。
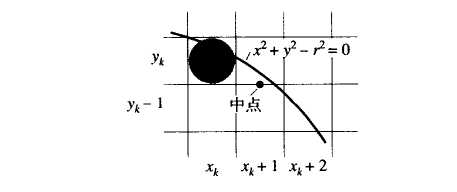
在第一象限上半1/8圆弧,如果已得到圆弧的象素点P(xp,yp),则下一可能的象素点是P1(xp+1,yp)和
P2(xp+1,yp-1)。究竟是P1还是P2 ,由P1和P2的中点M(xp+1,yp-0.5)的函数值F(xm,ym)来决定:
如果F(xm,ym)<0,说明圆弧在P1和M之间,取P1点为下一象素。
且下一象素的F(xp+2,yp-0.5)=F(xp+1,yp-0.5)+2xp+3
如果F(xm,ym)≥0,说明圆弧在P2和M之间,则取P2为下一象素。
且下一象素的F(xp+2,yp-1.5)=F(xp+1,yp-0.5)+2(xp-yp)+5
而F(1,r-0.5) = 1.25-r

分割凹多边形:

判断点是否在多边形内:
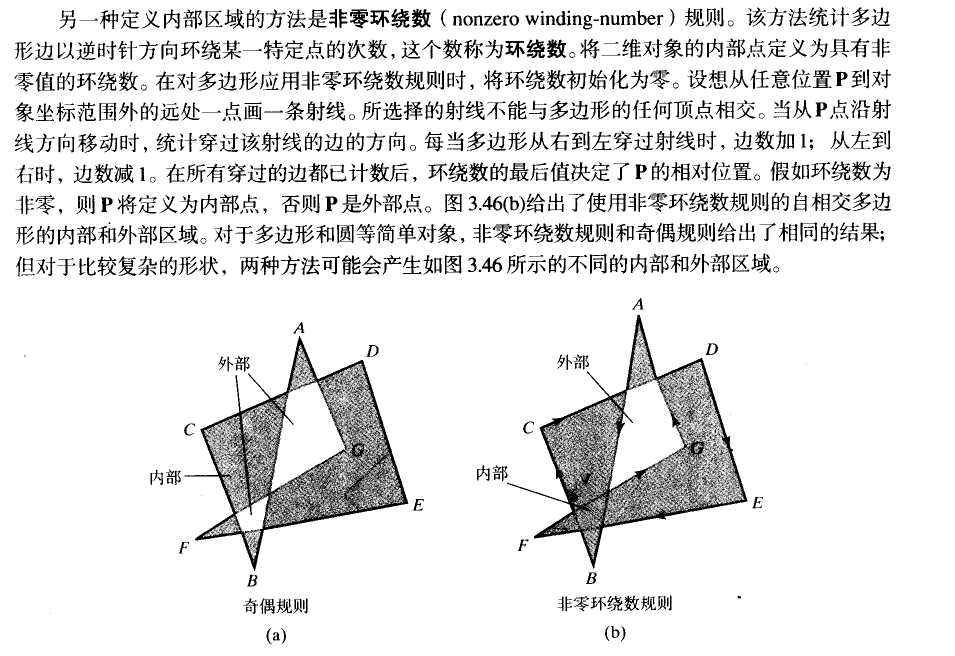
奇偶规则:从任一点P到对象范围以外的远点画一条射线,并统计该线与多边形的交点数目,当概数为奇数时,P时内部点,否则是外部点。
非零环绕数规则: