数据结构 Java版二叉排序树

时间：2018-01-16 14:00:20 阅读：190 评论：0 收藏：0 [点我收藏+]

　　二叉搜索树，又称为二叉查找树和二叉搜索树。它或者是一颗空树，或者具有下列性质的二叉树。

　　1 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值。

　　2 若它的右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值。

　　3 它的左、右子树也都为二叉搜索树。

　　构造一颗二叉搜索树，目的不是为了排序，而是为了提高查找、插入和删除关键字的速度。一个有序数据集上的查找速度总是要快于无序数据集，而二叉搜索树这种非线性的结构，也有利于插入和删除的实现。

　　二叉搜索树的查找性能取决于二叉搜索树的形状，问题在于二叉搜索树的形状是不确定的。例如{62, 88, 58, 47, 35, 73, 51, 99, 37, 93}，可以构建一棵正常的二叉搜索树。但是如果数组元素的次序是从小到大有序，如{35, 37, 47, 51, 58, 62, 73, 88, 93, 99}，则二叉搜索树就成了极端的单支树，依然是一棵二叉搜索树。查找结点99，左图只需要两次比较，而右图需要10次比较才能得到结果，差异很大。

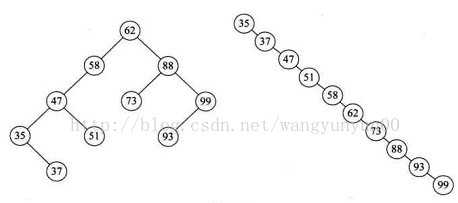
　　技术分享图片

　　二叉搜索树不一定是平衡的，即其深度与完全二叉树不一定相同。

// 实现了Comparable接口的元素可以通过compareTo方法来比较
public class BinarySearchTree<E extends Comparable<? super E>>

 1 // TreeNode静态嵌套类
 2 private static class TreeNode<E> {
 3     // 元素
 4     private E element;
 5     // 左孩子
 6     private TreeNode<E> left;
 7     // 右孩子
 8     private TreeNode<E> right;
 9     
10     private TreeNode(E e) {
11         element = e;
12         left = null;
13         right = null;
14     }
15 }

// 根结点
private BinarySearchTree<E> root;

// 无参构造方法
public BinarySearchTree() {
    root = null;
}

// 二叉搜索树置空
public void makeEmpty() {
    root = null;
}

// 判断树是否为空
public boolean isEmpty() {
    return root == null;
}

1 // 获取最小元素
2 public E findMin() {
3     if (isEmpty()) {
4         throw new NullPointerException();
5     }
6     
7     return findMin(root).element;
8 }

 1 // 子树上寻找最小值
 2 private TreeNode<E> findMin(TreeNode<E> treeNode) {
 3     if (treeNode == null) {
 4         return null;
 5     }
 6     
 7     while (treeNode.left != null) {
 8         treeNode = treeNode.left;
 9     }
10     
11     return treeNode;
12 }

1 // 获取最大元素
2 public E findMax() {
3     if (isEmpty()) {
4         throw new NullPointerException();
5     }
6     
7     return findMax(root).element;
8 }

 1 // 子树上寻找最大值
 2 private TreeNode<E> findMax(TreeNode<E> treeNode) {
 3     if (treeNode == null) {
 4         return null;
 5     }
 6     
 7     while (treeNode.right != null) {
 8         treeNode = treeNode.right;
 9     }
10     
11     return treeNode;
12 }

　　查找操作即判断是否包含指定元素：

　　先查找根结点，如果根结点的元素与指定元素相等，则返回true。否则，如果指定元素大于根结点，则查找右子树；如果小于根结点，则查找左子树。

// 判断是否包含指定元素
public boolean contains(E e) {
    return contains(root, e);
}

 1 // 判断是否包含指定元素
 2 private boolean contains(TreeNode<E> treeNode, E e) {
 3     if (treeNode == null) {
 4         return false;
 5     }
 6     
 7     while (treeNode != null) {
 8         int compareResult = e.compareTo(treeNode.element);
 9         if (compareResult == 0) {
10             return true;
11         } else if (compareResult < 0) {
12             treeNode = treeNode.left;
13         } else {
14             treeNode = treeNode.right;
15         }
16     }
17     
18     return false;
19 }

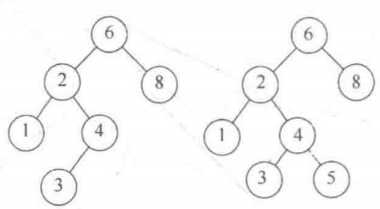
　　技术分享图片

　　插入5以前和以后的二叉搜索树

// 插入指定元素
public void insert(E e) {
    root = insert(root, e);
}

 1 // 子树上插入元素
 2 private TreeNode<E> insert(TreeNode<E> treeNode, E e) {
 3     if (treeNode == null) {
 4         return new TreeNode<E>(e, null, null);
 5     }
 6     
 7     int compareResult = e.compareTo(treeNode.element);
 8     if (compareResult < 0) {
 9         treeNode.left = insert(treeNode.left, e);
10     } else if (compareResult > 0) {
11         treeNode.right = insert(treeNode.right, e);
12     }
13     
14     return treeNode;
15 }

　　删除操作即删除第一次出现指定元素的结点，有3种情况：

　　1 叶子结点：直接删除即可。

　　2 仅有左或右子树的结点：上移子树即可。

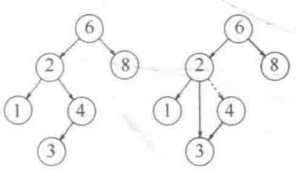
　　技术分享图片

　　结点4删除前后的情况

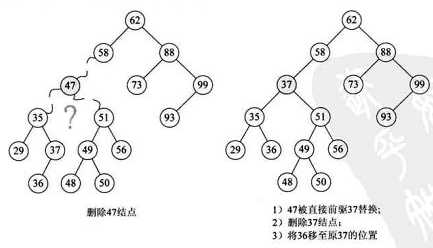
　　3 有左右子树的结点：用删除结点的直接前驱或者直接后继来替换当前结点，调整直接前驱或者直接后继的位置。

　　技术分享图片

// 刪除指定元素
public void remove(E e) {
    root = remove(root, e);
}

 1 // 子树上删除元素
 2 private TreeNode<E> remove(TreeNode<E> treeNode, E e) {
 3     if (treeNode == null) {
 4         return null;
 5     }
 6     
 7     int compareResult = e.compareTo(treeNode.element);
 8     TreeNode<E> l = treeNode.left, r = treeNode.right;
 9     if (compareResult < 0) {
10         treeNode.left = remove(l, e);
11     } else if (compareResult > 0) {
12         treeNode.right = remove(r, e);
13     } else if (l != null && r != null) {
14         treeNode.element = findMax(l).element;
15         treeNode.left = remove(treeNode.left, treeNode.element);
16     } else {
17         treeNode = (l != null) ? l : r;
18     }
19     
20     return treeNode;
21 }

1 // 遍历树
2 public void printTree() {
3     if (root == null) {
4         throw new NullPointerException();
5     }
6     
7     inorder(root);
8 }

 1 // 中序遍历
 2 private void inorder(TreeNode<E> treeNode) {
 3     if (treeNode == null) {
 4         return;
 5     }
 6     
 7     TreeNode<E> l = treeNode.left, r = treeNode.right;
 8     if (l != null) {
 9         inorder(l);
10     }
11     
12     System.out.print(" " + treeNode.element);
13     
14     if (r != null) {
15         inorder(r);
16     }
17 }

　　完整代码：

  1 // 实现了Comparable接口的元素可以通过compareTo方法来比较
  2 public class BinarySearchTree<E extends Comparable<? super E>> {
  3     // TreeNode静态嵌套类
  4     private static class TreeNode<E> {
  5         // 元素
  6         private E element;
  7         // 左孩子
  8         private TreeNode<E> left;
  9         // 右孩子
 10         private TreeNode<E> right;
 11         
 12         private TreeNode(E e) {
 13             element = e;
 14             left = null;
 15             right = null;
 16         }
 17     }
 18     
 19     // 根结点
 20     private TreeNode<E> root;
 21     
 22     // 无参构造方法
 23     public BinarySearchTree() {
 24         root = null;
 25     }
 26     
 27     // 二叉搜索树置空
 28     public void makeEmpty() {
 29         root = null;
 30     }
 31     
 32     // 判断树是否为空
 33     public boolean isEmpty() {
 34         return root == null;
 35     }
 36     
 37     // 判断是否包含指定元素
 38     public boolean contains(E e) {
 39         return contains(root, e);
 40     }
 41     
 42     // 获取最小元素
 43     public E findMin() {
 44         if (isEmpty()) {
 45             throw new NullPointerException();
 46         }
 47         
 48         return findMin(root).element;
 49     }
 50     
 51     // 获取最大元素
 52     public E findMax() {
 53         if (isEmpty()) {
 54             throw new NullPointerException();
 55         }
 56         
 57         return findMax(root).element;
 58     }
 59         
 60     // 插入指定元素
 61     public void insert(E e) {
 62         root = insert(root, e);
 63     }
 64     
 65     // 刪除指定元素
 66     public void remove(E e) {
 67         root = remove(root, e);
 68     }
 69         
 70     // 遍历树
 71     public void printTree() {
 72         if (root == null) {
 73             throw new NullPointerException();
 74         }
 75         
 76         inorder(root);
 77     }
 78     
 79     // 判断子树上是否包含指定元素
 80     private boolean contains(TreeNode<E> treeNode, E e) {
 81         if (treeNode == null) {
 82             return false;
 83         }
 84         
 85         while (treeNode != null) {
 86             int compareResult = e.compareTo(treeNode.element);
 87             if (compareResult == 0) {
 88                 return true;
 89             } else if (compareResult < 0) {
 90                 treeNode = treeNode.left;
 91             } else {
 92                 treeNode = treeNode.right;
 93             }
 94         }
 95         
 96         return false;
 97     }
 98     
 99     // 子树上寻找最小值
100     private TreeNode<E> findMin(TreeNode<E> treeNode) {
101         if (treeNode == null) {
102             return null;
103         }
104         
105         while (treeNode.left != null) {
106             treeNode = treeNode.left;
107         }
108         
109         return treeNode;
110     }
111     
112     // 子树上寻找最大值
113     private TreeNode<E> findMax(TreeNode<E> treeNode) {
114         if (treeNode == null) {
115             return null;
116         }
117         
118         while (treeNode.right != null) {
119             treeNode = treeNode.right;
120         }
121         
122         return treeNode;
123     }
124         
125     // 子树上插入元素
126     private TreeNode<E> insert(TreeNode<E> treeNode, E e) {
127         if (treeNode == null) {
128             return new TreeNode<E>(e);
129         }
130         
131         int compareResult = e.compareTo(treeNode.element);
132         if (compareResult < 0) {
133             treeNode.left = insert(treeNode.left, e);
134         } else if (compareResult > 0) {
135             treeNode.right = insert(treeNode.right, e);
136         }
137         
138         return treeNode;
139     }
140     
141     // 子树上删除元素
142     private TreeNode<E> remove(TreeNode<E> treeNode, E e) {
143         if (treeNode == null) {
144             return null;
145         }
146         
147         int compareResult = e.compareTo(treeNode.element);
148         TreeNode<E> l = treeNode.left, r = treeNode.right;
149         if (compareResult < 0) {
150             treeNode.left = remove(l, e);
151         } else if (compareResult > 0) {
152             treeNode.right = remove(r, e);
153         } else if (l != null && r != null) {
154             treeNode.element = findMax(l).element;
155             treeNode.left = remove(treeNode.left, treeNode.element);
156         } else {
157             treeNode = (l != null) ? l : r;
158         }
159         
160         return treeNode;
161     }
162     
163     // 中序遍历
164     private void inorder(TreeNode<E> treeNode) {
165         if (treeNode == null) {
166             return;
167         }
168         
169         TreeNode<E> l = treeNode.left, r = treeNode.right;
170         if (l != null) {
171             inorder(l);
172         }
173         
174         System.out.print(" " + treeNode.element);
175         
176         if (r != null) {
177             inorder(r);
178         }
179     }
180     
181     public static void main(String[] args) {
182         BinarySearchTree<String> binarySearchTree = new BinarySearchTree<String>();
183         String[] key = {"62", "88", "58", "47", "35", "73", "51", "99", "37", "93"};
184         for (int i = 0; i < 10; i++) {
185             binarySearchTree.insert(key[i]);
186         }
187         
188         System.out.println("中序遍历结果：");
189         binarySearchTree.printTree();
190         System.out.println();
191         
192         binarySearchTree.remove("58");
193         System.out.println("删除58后中序遍历结果：");
194         binarySearchTree.printTree();
195         System.out.println();
196     }
197 }

　　输出结果：

中序遍历结果：
 35 37 47 51 58 62 73 88 93 99
删除58后中序遍历结果：
 35 37 47 51 62 73 88 93 99

　　参考资料

　　二叉排序树（查询、插入、删除）

　　《数据结构与算法分析Java语言描述原书第3版》 P78-86

数据结构 Java版二叉排序树

标签：代码查找 pareto java 分享算法分析 rgs 参考资料相同

原文地址：https://www.cnblogs.com/WJQ2017/p/8290298.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行