1. 完全二叉树:叶节点只能出现在最后层或次下层,并且最下面一层的节点都集中在该层的最左边的二叉树。
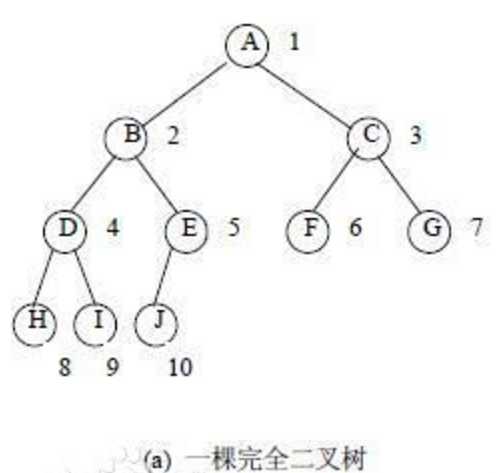
2. 二叉堆:堆是一颗二叉树,并且满足下面的条件:
(1)树的每一层都是满,除了最后一层的最右边元素
(2)任意一个父节点都大于或等于(小于或等于)两个子节点。(大于或等于的为最大堆,小于或等于的为最小堆)
(3)每个结点的左子树或右子树都是二叉堆(最大堆或最小堆)
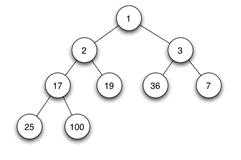
最小堆 堆的形状
3. 堆的存储:
使用数组的方式存储(从下标0开始),每个父节点的左右子节点为2*i+1 和 2*i+2,子节点的父节点为(i-1)/2。
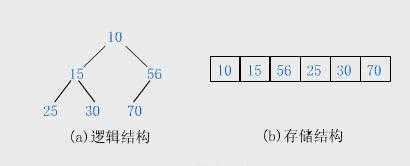
4. C++实现最小堆:
/*最小堆的插入节点*/ void MinHeapInsertNum(std::vector<int> & a, int num) { /* 把插入的元素放在堆的最后面,通过自底向上的不断上潜,来插入新元素 */ /* 由于堆的高度为log(n),所以插入效率是O(log(n)) */ a.push_back(num); //尾结点插入元素 int tmp = a[a.size()-1]; //tmp为要插入的元素的值 int i = a.size()-1; //i是子节点 int j = (i-1)/2; //j是父节点 while(j>=0 && i!=0) //i必须不等于0 因为 j=(int)0-0.5=0,会无限循环 { if(tmp >= a[j]) //如果是最大堆的插入,则改为: if(tmp <= a[j]) break; else { a[i] = a[j]; //父节点值比子节点大,所以父节点的值要下堆到子节点的位置。 i = j; //子节点上移 j = (i-1)/2; //父节点上移 } } a[i] = tmp; //父节点下堆完成后,把新元素插入在符合要求的位置(某个父节点下的子节点位置) } /*最小堆的删除根节点*/ int MinHeapDeleteNum(std::vector<int> & a) { /* 将根节点和尾结点交换位置后,删除尾节点,之后根节点自顶向下不断下潜,来完成堆*/ /* 根节点的每次下潜要与左右子节点比较,即总共2*log(n)的比较次数,所有删除效率为O(log(n))*/ //头结点与尾结点交换位置 std::swap(a[0],a[a.size()-1]); //将最后一个元素释放,即释放了头结点 a.pop_back(); //现在的头结点从上向下沉,即数据下沉堆化 int tmp = a[0]; int i = 0; //i为父节点 int j = i*2+1; //j为子节点 while(j<a.size()) { //找出当前父节点的左右子节点中,最小的那个 if( (j+1) < (a.size()-1) && a[j+1]<a[j] ) ++j; if(tmp<=a[j]) //找到了头结点的正确位置 break; else { a[i] = a[j]; //子节点的值比父节点小,所以子节点要上堆到当前父节点的位置 i = j; //父节点下移 j = i*2+1; //子节点下移 } } a[i] = tmp; //子节点上堆完成后,将原始堆的尾结点放在适当的位置 return HeadNum; } /*最小堆的堆化*/ void MakeMinHeap(std::vector<int> & a) { /* 从原始树的次下层开始,每一个元素都自顶向下地下潜(若该元素比子节点大,则该元素下潜)*/ /* 在最坏的情况下,总的比较次数是2(n-log(n+1)),所有堆化效率是O(n) */ //所有子堆进行自顶往下的堆化 for(int k=a.size()/2-1; k>=0; k--) { int tmp = a[k]; int i = k; //i为父节点 int j = i*2+1; //j为子节点 while(j<a.size()) { //找出子节点中最小的那个 if( (j+1) < (a.size()-1) && a[j+1]<a[j] ) ++j; if(tmp<=a[j]) break; else { a[i] = a[j]; //子节点的值比父节点小,所以子节点要上堆到当前父节点的位置 i = j; //父节点下移 j = i*2+1; //子节点下移 } } a[i] = tmp; } }
5. 堆排序:
将普通的二叉树构建成一颗最小堆,依次删除最小堆的根节点,得到的出队顺序就是堆排序的结果。实现代码如下:
/*最小堆出队顺序为从小到大*/ std::vector<int> MinHeapSort(std::vector<int> & a) { /* ① 构造堆 ② 删除堆的根节点,即对剩下的堆删除n-1次根节点,得到的输出序列就是堆排序结果 */ /* 构造堆的效率为O(n),删除堆根节点的总效率为O(nlog(n)),所以总效率为O(nlog(n))*/ std::vector<int> res; while(!a.empty()) { res.push_back(MinHeapDeleteNum(a)); } return res; }
