0.背景
Tim Salimans等人认为之前的GANs虽然可以生成很好的样本,然而训练GAN本质是找到一个基于连续的,高维参数空间上的非凸游戏上的纳什平衡。然而不幸的是,寻找纳什平衡是一个十分困难的问题。在现有的针对特定场景算法中,找不适合GAN游戏的算法,因为GAN的实现通常是使用梯度下降的方法去训练GAN网络的目标函数,而不是真的找零和游戏中的纳什平衡。且目标函数本身是非凸函数,其中是连续参数且参数空间维度很高,所以如果真的去搜寻纳什平衡,那么这些算法都是无法收敛的。
当游戏中每个人都认为自己当前是最小损失的时候,那么就是达到了纳什平衡。这直观的让我们认为,可以使用传统的基于梯度最小化的方法去同时最小化每个人的损失函数。即,假设判别器和生成器的损失函数为:\(J^{(D)}(\theta^{(D)},\theta^{(G)})\);\(J^{(G)}(\theta^{(D)},\theta^{(G)})\)。纳什平衡的点\((\theta^{(D)},\theta^{(G)})\)上,\(J^{(D)}\)关于\(\theta^{(D)}\)最小且\(J^{(G)}\)关于\(\theta^{(G)}\)最小。不过这基本很难实现,因为当修改\(\theta^{(D)}\)且降低\(J^{(D)}\)时,会增加\(J^{(G)}\),而修改\(\theta^{(G)}\)且降低\(J^{(G)}\)时,会增加\(J^{(D)}\),因此梯度下降就无法收敛了。举个例子:
- 一个游戏者的目标函数是xy,其参数为x;
- 另一个游戏者的目标函数是-xy,其参数是y
梯度下降会遇到一个稳定的点,而不是收敛到x=y=0(理想的平衡点)。
总结来说,就是之前基于梯度下降训练GAN的方法同时最小化每个游戏者的损失函数,是缺乏他们都收敛的保证的。所以Tim Salimans等人提出了三个有利于模型训练的方法,意在能够较好的收敛:
- feature matching:类似于最大均值差异
- minibatch features:借鉴于部分bn的想法
- virtual batch normalization:bn的一个扩展
1. 三个提出的建议
1.1 特征匹配
特征匹配是通过在生成器上指定一个新目标,从而防止在当前判别器基础上过度训练的问题。不是简单的最大化判别器的输出,而是让生成器生成的数据能够匹配真实数据的统计特征。这其中,判别器只需要指定哪些统计特征需要匹配。具体来说,Salimans等人通过让生成器去匹配判别器中间层上的特征值。即:
让\(f(x)\)表示判别器中间层的激活值,生成器新的目标就是\(||E_{x\sim p_{data}}f(x)-E_{z\sim p_{z(z)}}f(G(z))||^2_2\)。其中判别器的\(f(x)\)还是按照以往方法训练。新的目标函数可以让生成器有个固定点,该点可以准确的匹配训练数据的分布,虽然理论上无法保证达到这个固定点,不过实验中显示这的确有助于传统的GAN训练变得稳定高效。
1.2 minibatch discrimination
在GAN的训练中,一个主要的失败状况就是生成器会陷入一个parameter setting,且该位置总是输出相同的点。当生成器陷入这种情况时,判别器的梯度总是会指向相似的方向,从而没有判别性,生成器也就只生成同一类同一个结果了。因为判别器是单独处理每个样本的,所以梯度之间就没有方向等坐标信息,所以没法说当前生成器的输出和另一个输出之间有多不同。即此时判别器只能识别真假,却不能识别是不是来自生成器的同一个输出。
Salimans等人认为通过让判别器同时判别多个样本,从而能够避免掉这类问题,即“minibatch discrimination”。
- 假设第i个输入为\(x_i\);
- \(f(x_i)\in R^A\)表示判别器中间层输出的特征向量;
- 将其乘以一个张量\(T\in R^{A\times B\times C}\),从而生成矩阵\(M_i\in R^{B\times C}\);
- 基于不同的样本生成的矩阵\(M_i\),\(i\in \{1,2,...,n\}\)的行之间计算\(L_1\)距离:
\(c_b(x_i,x_j)=exp\left(-||M_{i,b}-M_{j,b}||_{L_1}\right)\in R\)
其中b表示矩阵的第b行;- 这minibatch layer中关于样本\(x_i\)的输出\(o(x_i)\)定义为,样本\(x_i\)与其他样本之间的\(c_b(x_i,x_j)\)的和:
\(o(x_i)_b=\sum_{j=1}^nc_b(x_i,x_j)\in R\)
\(o(x_i)=\left[o(x_i)_1,o(x_i)_2,...,o(x_i)_B\right]\in R^B\)
\(o({\bf X}\in R^{n\times B})\)
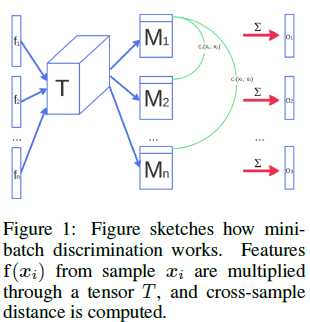
如上述步骤所述,最后是将每个样本得到的\(o(x_i)\)按照行进行堆叠得到\(o({\bf X})\),然后将其输入到下一层判别器的网络层。在进行minibatch discrimination是分别计算伪造数据和真实数据的(即在一个minibatch中不存在同时具有伪造数据和真实数据)。同样的,判别器需要对每个样本输出其为真的概率,不过现在借助于minibatch中其他样本的信息,即side information。从而让生成器更快的生成视觉可接受的伪造数据,在这方面,它优于特征匹配。不过有趣的是,当在半监督学习中,你所需要的目标是为了获得一个强分类器,那么特征匹配的方法更好。
1.3 历史平均(Historical averaging)
当使用历史平均的方法时,每个游戏者的损失函数会包含一项\(||\theta-\frac{1}{t}\sum_{i=1}^t\theta[i]||^2\),这里\(\theta[i]\)表示在时间为\(i\)时候的参数值。参数的历史平均可以采用在线更新的方式,所以学习规则可以适用于很长的时间序列。该方法是受到《Iterative solution of games by fictitious play》中fictitious play算法的启发。Salimans等人等人发现该方法可以在低维,连续的非凸游戏中找到平衡,如一个最小最大游戏,其中一个游戏者控制x,另一个游戏者控制y,值函数为:
\[(f(x)-1)(y-1),
\begin{cases}
f(x)=x,& x<0\f(x)=x^2,& otherwise
\end{cases}
\]
而在此类toy类的游戏中,梯度下降方法因为找不到平衡点,从而失效。
1.4 One-sided label smoothing
标签平滑方法最初来自1980s,近年来重新被使用。主要就是将分类器的0和1替换成更平滑的值,如0.1和0.9。此方法也可以增加神经网络对 对抗样本的鲁棒性。
即将正类结果乘以\(\alpha\),负类结果乘以\(\beta\),从而最优分类器变成:
\[D(x)=\frac{\alpha p_{data}(x)+\beta p_model(x)}{p_{data}(x)+p_{model}(x)}\]
不过分子中的\(p_{model}\)是有问题的,因为当\(p_{data}\)接近于0,而\(p_{model}\)又很大的时候,来自\(p_{model}\)的错误样本没法让模型参数更靠近数据(即让网络学到真实数据的分布)。因而只平滑正样本到\(\alpha\),让负样本到0(即不平滑负类)
1.5 虚拟bn(virtual batch normalization)
BN极大的提升了神经网络的优化过程,不过它会导致一个输入样本在神经网络输出的时候极大的依赖minibatch中其他的输入。为了避免这个问题,从而引入了VBN,在这其中每个样本都是基于一批引用样本(reference batch)的统计信息基础上进行归一化的,这批引用样本一旦在训练开始选中,在整个过程都会引用。这批引用样本自己的归一化当然也是基于自己这批引用样本。VBN计算代价比较大,因为他需要在前向传播中读取两个minibatch数据,所以这个方法只用在生成网络中。
2.图像质量评估
GAN因为缺少一个目标函数,从而无法将其与其他模型进行性能上的比较。一个直观的性能度量就是让人来评价样本的视觉质量。不过当样本量太大的时候,该方法不可行;一个替代的方法就是期望用其他模型来评估伪造数据的质量:用inception模型去计算每一张生成样本的条件标签分布\(p(y|x)\)。期望
- 包含有意义对象的图像其条件标签分布的熵会比较低;
- 模型生成的不同图片的边缘分布\(\int p(y|x=G(z))dz\)会有高熵。
将这两个要求组合起来,度量方法就是:\(exp(E_xKL(p(y|x)||P(y)))\),从而值就能够较容易的比较了。该方法无法成功的作为一个对象去训练,不过却是一个很好的用来代替人工评估的度量方法。
3.半监督学习
对于通常的多分类,就是\(p_{model}(y=j|x)=\frac{exp(l_j)}{\sum_{k=1}^Kexp(l_k)}\)。对于有监督学习,这样一个模型就通过最大化真实标签和模型给的标签\(p_{model}(y|x)\)之间的交叉熵。
而对于标准分类器的半监督学习,就是将GAN生成器生成的样本增加到数据集中,也就是将生成的数据标记为一个新的"生成"类,\(y=K+1\),对应的让分类器的输出维度从K到K+1。然后使用\(p_{model}(y=K+1|x)\)来提供当前输入样本是伪造的概率(对应GAN结构中\(1-D(x)\))。现在我们也可以从无标签数据中学习了,且是通过最大化\(logp_{model}(y \in\{1,...K\}|x)\)得到的。假设数据集中一半是真实数据,一半是生成数据,那么训练分类器的损失函数为:
\[L=-E_{x,y\sim p_{data}\; (x,y)}\left[logp_{model}(y|x)\right]-E_{x\sim G}\left[\log p_{model}(y=K+1|x)\right]\]
将其分成2个部分即:
其中:
将总的交叉熵损失函数分成标准的有监督损失函数和无监督损失函数,其中无监督损失函数就是标准的GAN网络\(D(x)=1-p_{model}(y=K+1|x)\)代入:
同时最小化有监督损失和无监督损失的最优解的方法是:基于某个缩放函数\(c(x),有\)\(exp[l_j(x)]=c(x)p(y=j,x)\forall j<K+1\)和\(exp[l_{K+1}(x)]=c(x)P_G(x)\),从而让无监督损失和有监督损失保持一致,通过同时最小化这两个损失函数从而达到最优解。在实际操作中,\(L_{unsupervised}\)只有在最小化分类器不麻烦的情况下才有帮助,所以需要训练G来逼近真实数据分布。一种方法是使用分类器作为判别器D,训练G从而最小化GAN网络的值。Salimans等人虽然还未明白G与分类器之间的关系,不过实验显示在无监督学习中,使用特征匹配的方式优化G效果很好,而使用minibatch discriminiation就一点效果都没。
这里的K+1的分类器有点过参数化了。如果对每个输出logit都减去一个函数\(f(x)\),即\(l_j(x)\leftarrow l_j(x)-f(x)\forall j\)。也不会改变softmax的输出。这也就是说等效的\(l_{K+1}(x)=0\forall x\),从而\(L_{supervised}\)变成K个类别的有监督损失函数,从而判别器为\(D(x)=\frac{Z(x)}{Z(x)+1}\),其中\(Z(x)=\sum_{k=1}^Kexp[l_k(x)]\).
