原博来自http://www.cnblogs.com/skywang12345/
弗洛伊德算法介绍
和Dijkstra算法一样,弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
基本思想
通过Floyd计算图G=(V,E)中各个顶点的最短路径时,需要引入一个矩阵S,矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。
假设图G中顶点个数为N,则需要对矩阵S进行N次更新。初始时,矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞。 接下来开始,对矩阵S进行N次更新。第1次更新时,如果"a[i][j]的距离" > "a[i][0]+a[0][j]"(a[i][0]+a[0][j]表示"i与j之间经过第1个顶点的距离"),则更新a[i][j]为"a[i][0]+a[0][j]"。 同理,第k次更新时,如果"a[i][j]的距离" > "a[i][k]+a[k][j]",则更新a[i][j]为"a[i][k]+a[k][j]"。更新N次之后,操作完成!
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
弗洛伊德算法图解
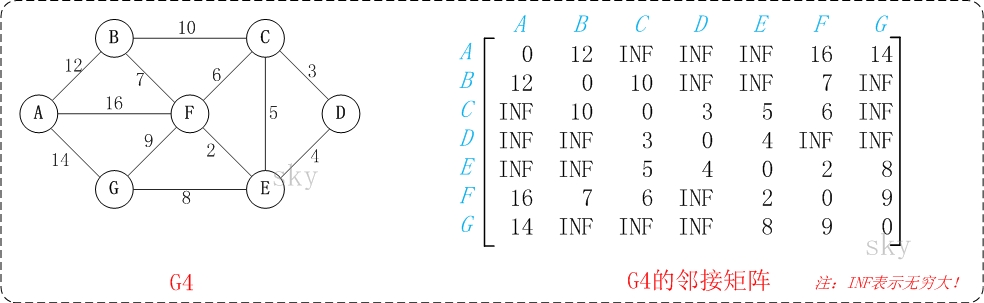
以上图G4为例,来对弗洛伊德进行算法演示。
初始状态:S是记录各个顶点间最短路径的矩阵。
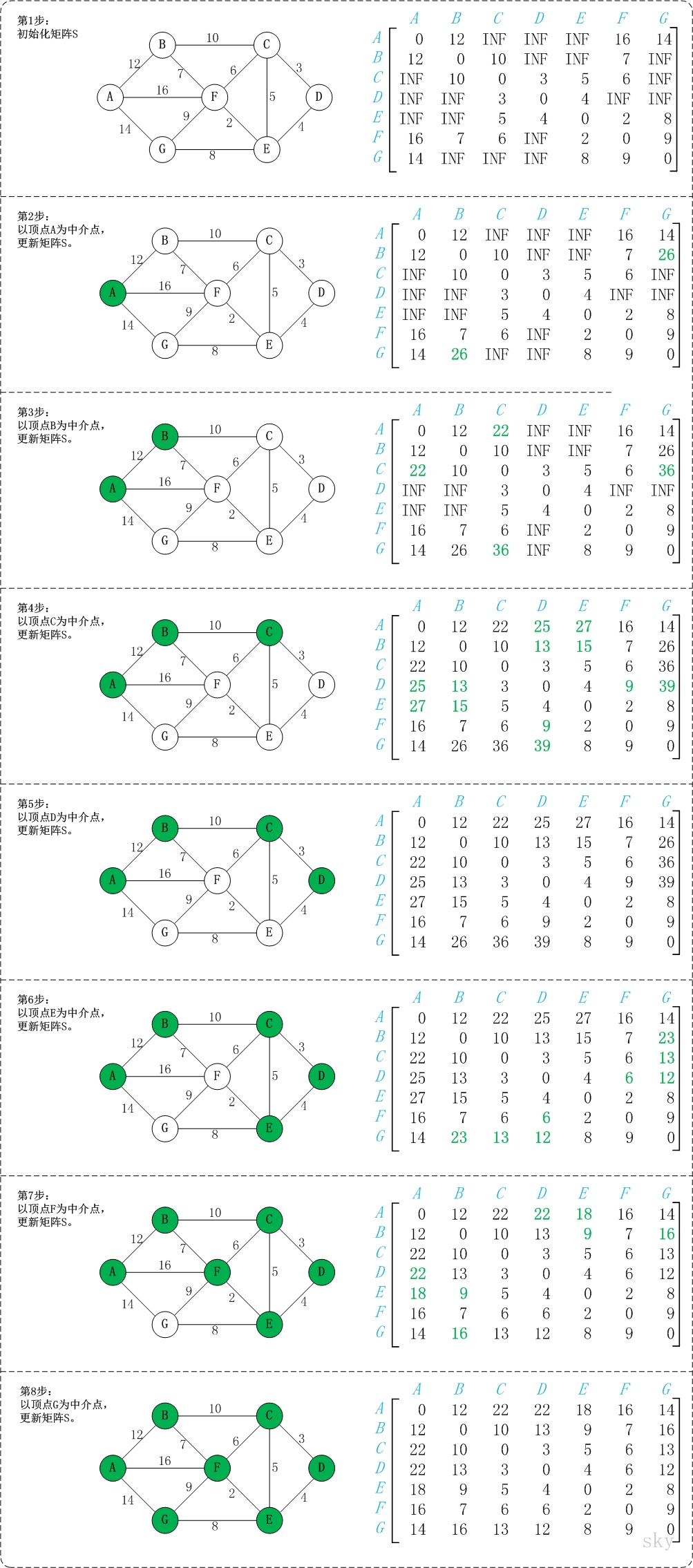
第1步:初始化S。
矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞。实际上,就是将图的原始矩阵复制到S中。
注:a[i][j]表示矩阵S中顶点i(第i个顶点)到顶点j(第j个顶点)的距离。
第2步:以顶点A(第1个顶点)为中介点,若a[i][j] > a[i][0]+a[0][j],则设置a[i][j]=a[i][0]+a[0][j]。
以顶点a[1]6,上一步操作之后,a[1][6]=∞;而将A作为中介点时,(B,A)=12,(A,G)=14,因此B和G之间的距离可以更新为26。
同理,依次将顶点B,C,D,E,F,G作为中介点,并更新a[i][j]的大小。
弗洛伊德算法的代码说明
以"邻接矩阵"为例对弗洛伊德算法进行说明,对于"邻接表"实现的图在后面会给出相应的源码。
1. 基本定义
1 // 邻接矩阵 2 typedef struct _graph 3 { 4 char vexs[MAX]; // 顶点集合 5 int vexnum; // 顶点数 6 int edgnum; // 边数 7 int matrix[MAX][MAX]; // 邻接矩阵 8 }Graph, *PGraph;
Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
2. 弗洛伊德算法
1 /* 2 * floyd最短路径。 3 * 即,统计图中各个顶点间的最短路径。 4 * 5 * 参数说明: 6 * G -- 图 7 * path -- 路径。path[i][j]=k表示,"顶点i"到"顶点j"的最短路径会经过顶点k。 8 * dist -- 长度数组。即,dist[i][j]=sum表示,"顶点i"到"顶点j"的最短路径的长度是sum。 9 */ 10 void floyd(Graph G, int path[][MAX], int dist[][MAX]) 11 { 12 int i,j,k; 13 int tmp; 14 15 // 初始化 16 for (i = 0; i < G.vexnum; i++) 17 { 18 for (j = 0; j < G.vexnum; j++) 19 { 20 dist[i][j] = G.matrix[i][j]; // "顶点i"到"顶点j"的路径长度为"i到j的权值"。 21 path[i][j] = j; // "顶点i"到"顶点j"的最短路径是经过顶点j。 22 } 23 } 24 25 // 计算最短路径 26 for (k = 0; k < G.vexnum; k++) 27 { 28 for (i = 0; i < G.vexnum; i++) 29 { 30 for (j = 0; j < G.vexnum; j++) 31 { 32 // 如果经过下标为k顶点路径比原两点间路径更短,则更新dist[i][j]和path[i][j] 33 tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]); 34 if (dist[i][j] > tmp) 35 { 36 // "i到j最短路径"对应的值设,为更小的一个(即经过k) 37 dist[i][j] = tmp; 38 // "i到j最短路径"对应的路径,经过k 39 path[i][j] = path[i][k]; 40 } 41 } 42 } 43 } 44 45 // 打印floyd最短路径的结果 46 printf("floyd: \n"); 47 for (i = 0; i < G.vexnum; i++) 48 { 49 for (j = 0; j < G.vexnum; j++) 50 printf("%2d ", dist[i][j]); 51 printf("\n"); 52 } 53 }
完整代码可以见:http://www.wutianqi.com/?p=1903