ps：本博客内容根据唐宇迪的的机器学习经典算法  学习视频复制总结而来

http://www.abcplus.com.cn/course/83/tasks

逻辑回归

问题描述：我们将建立一个逻辑回归模型来预测一个学生是否被大学录取。假设你是一个大学系的管理员，你想根据两次考试的结果来决定每个申请人的录取机会。你有以前的申请人的历史数据，你可以用它作为逻辑回归的训练集。对于每一个培训例子，你有两个考试的申请人的分数和录取决定。为了做到这一点，我们将建立一个分类模型，根据考试成绩估计入学概率。

数据下载：https://pan.baidu.com/s/1pNbtrjP

数据大概长这个样

1、查看数据基本属性

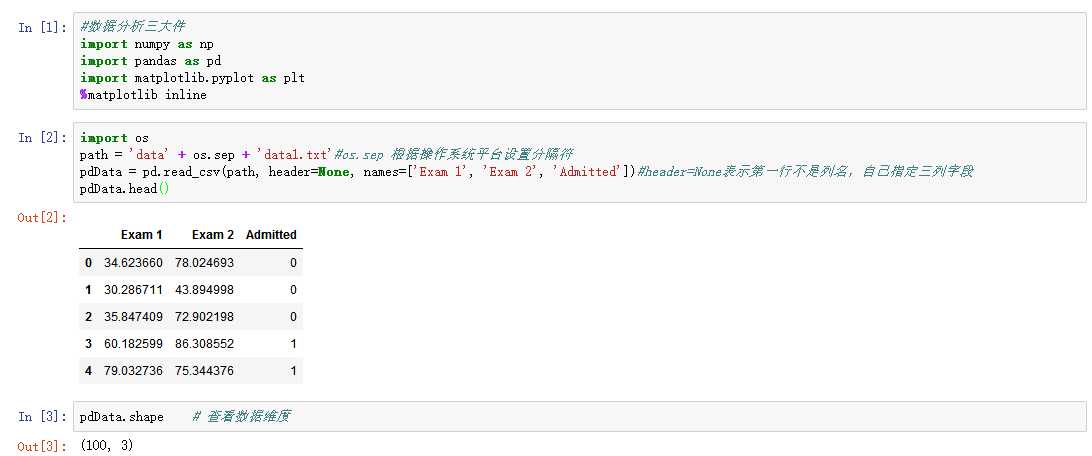
2、画图观察

plot结构剖析

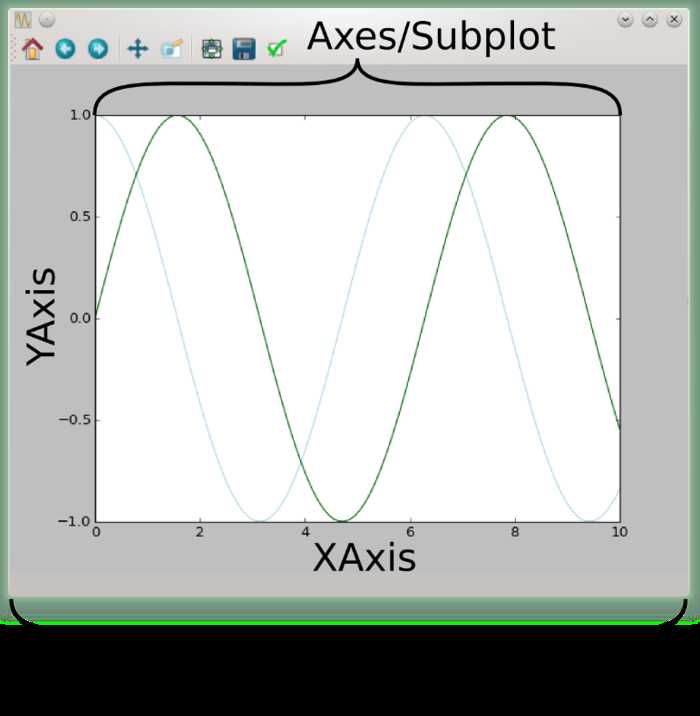
上图来自https://www.jianshu.com/p/b4b5dd20e48a

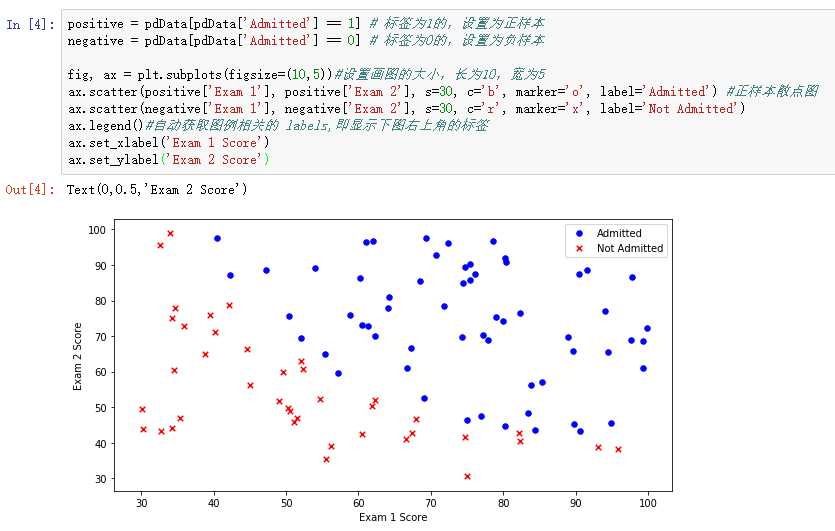
3、建立分类器（求解出三个参数 θ0、θ1、θ2）

设定阈值，根据阈值判断录取结果（此处设置为50%，≥50%即判断录取）

要完成的模块： 
- sigmoid : 映射到概率的函数

• model : 返回预测结果值

• cost : 根据参数计算损失

• gradient : 计算每个参数的梯度方向

• descent : 进行参数更新

• accuracy: 计算精度

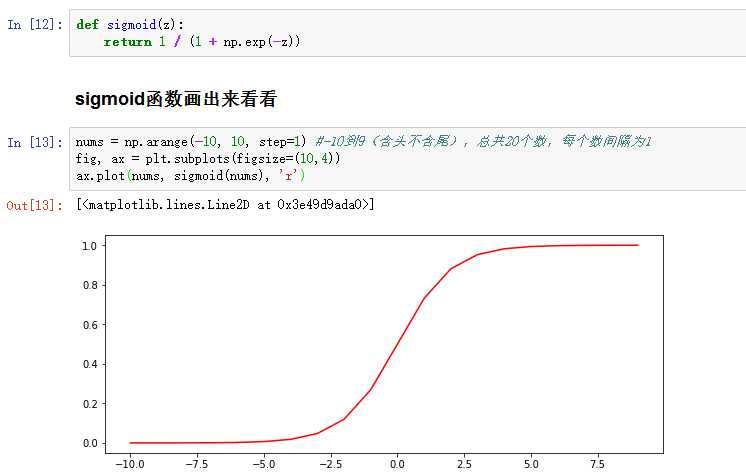
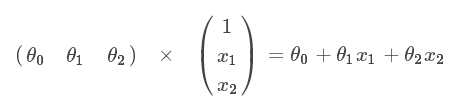
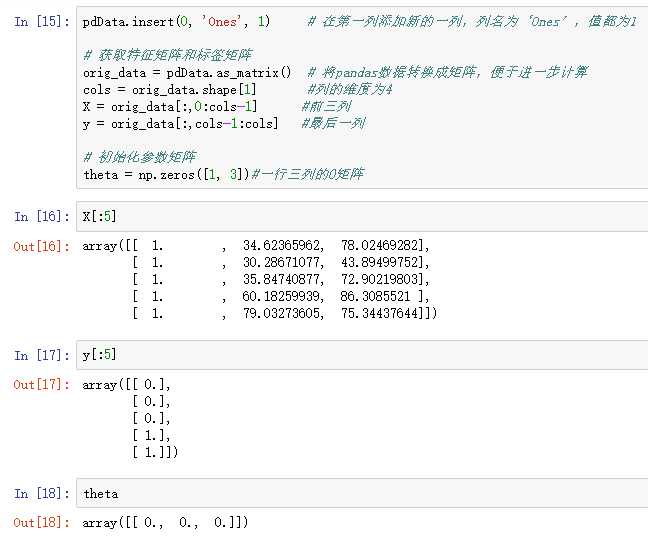
4、损失函数 

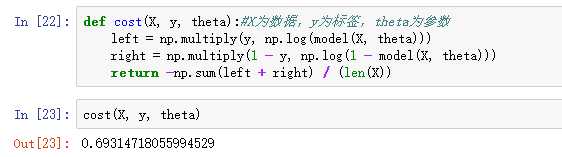
5、计算梯度

6、梯度下降（比较三种梯度下降方法）

下面这段代码仅仅是将过程可视化

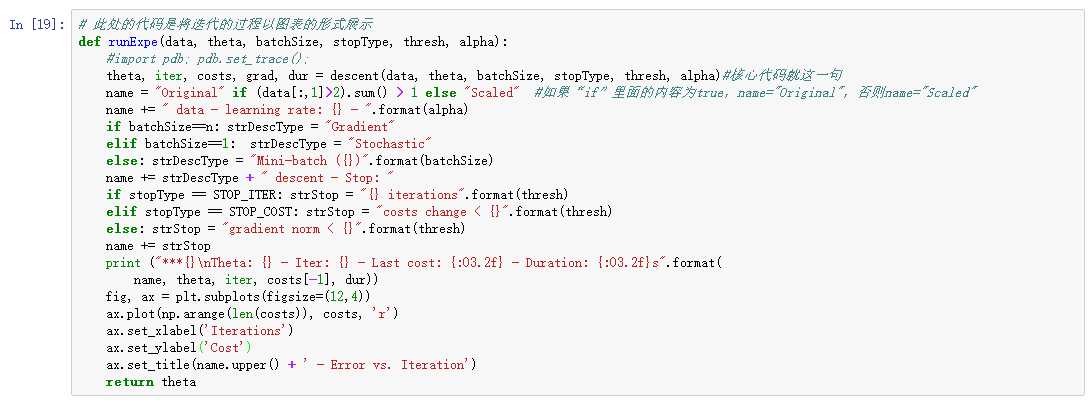
7、不同的停止策略

①设定迭代次数

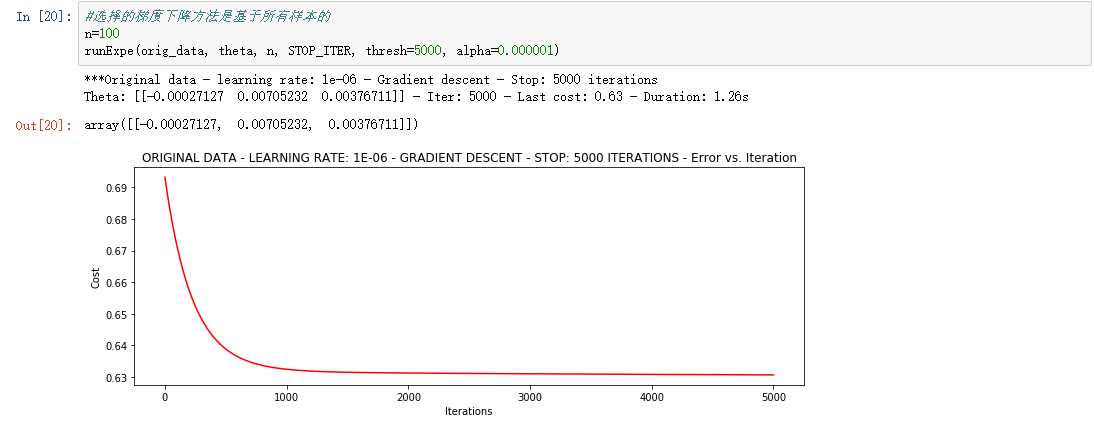
②根据损失值停止

上面的迭代次数过少，修改阈值为1E-6，迭代次数大概需要110000次 。会发现值再次降低

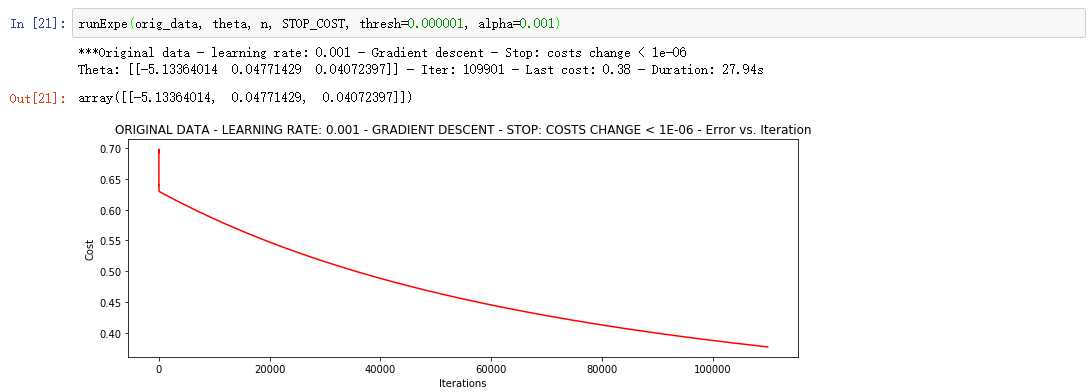
这种策略虽然准确度较高，但是迭代次数多，计算量大

③、根据梯度变化停止

设定阈值 0.05,差不多需要40 000次迭代

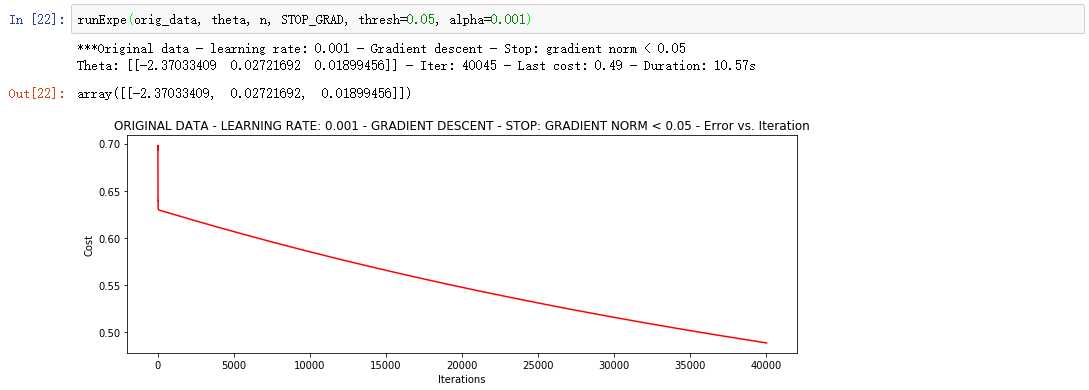
8、对比不同的梯度下降方法

 ①Stochastic descent  随机梯度下降

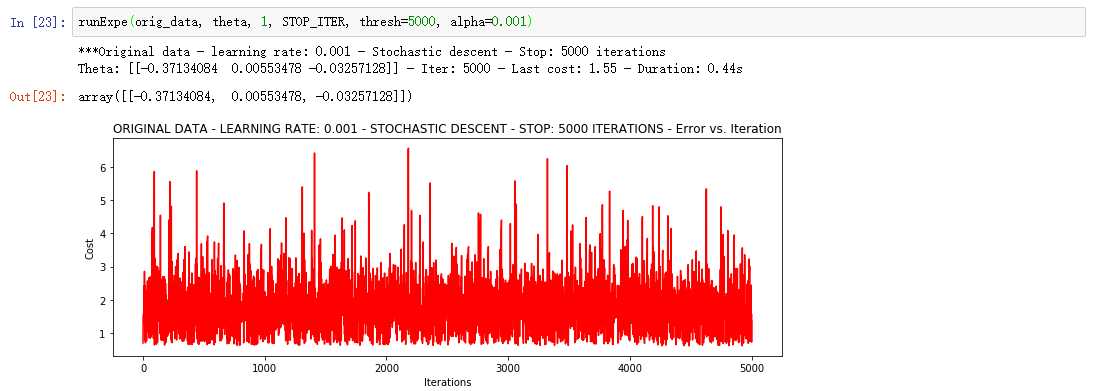
相当不稳定,再来试试把学习率调小一些

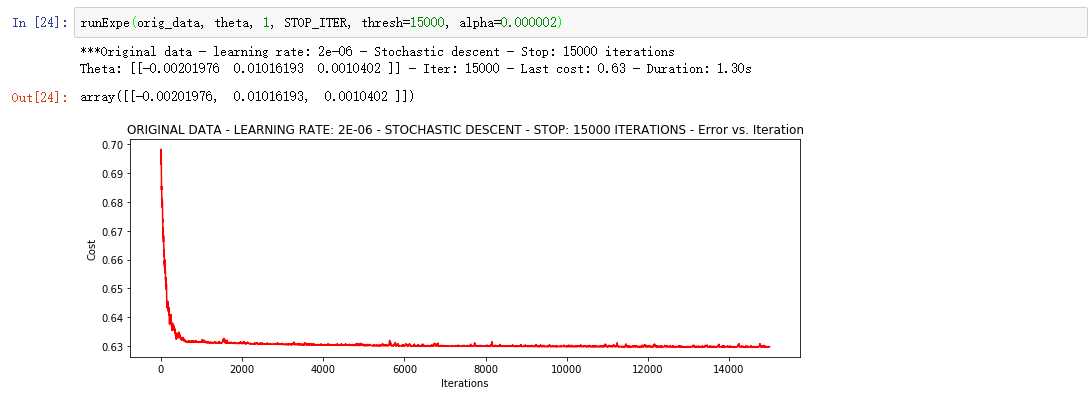
速度快，效果和稳定性都差，需要很小的学习率

②Mini-batch descent 小批量梯度下降

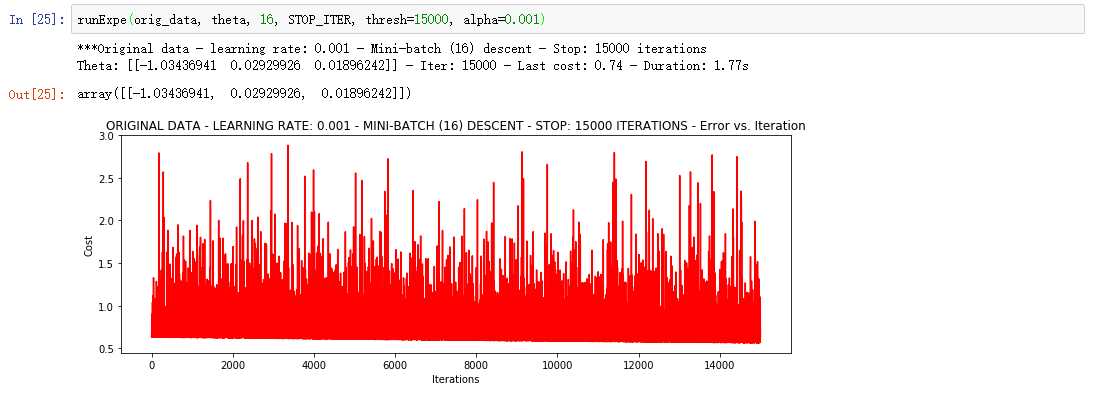
标准化/归一化

浮动仍然比较大，我们来尝试下对数据进行标准化 将数据按其属性(按列进行)减去其均值，然后除以其方差。最后得到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1。

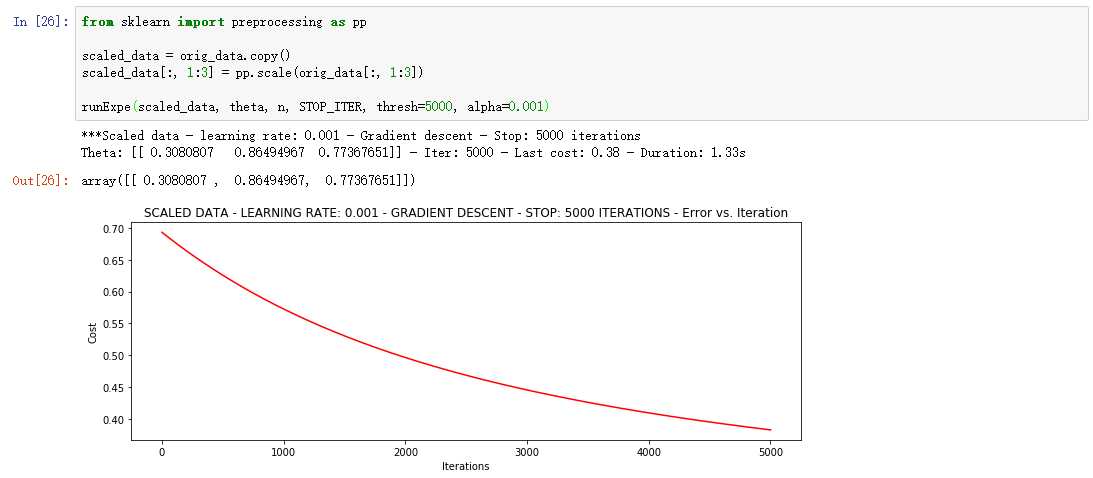
它好多了！原始数据，只能达到达到0.61，而我们得到了0.38个在这里！ 所以对数据做预处理是非常重要的。

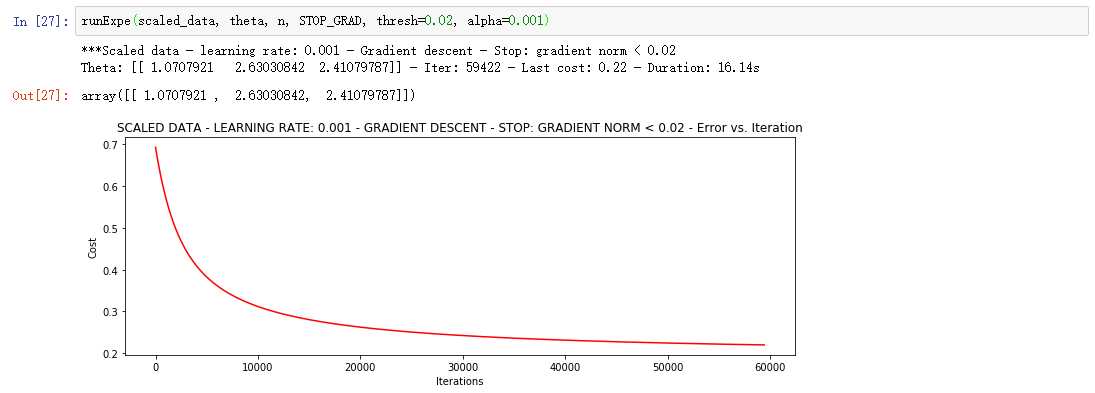
更多的迭代次数会使得损失下降的更多！

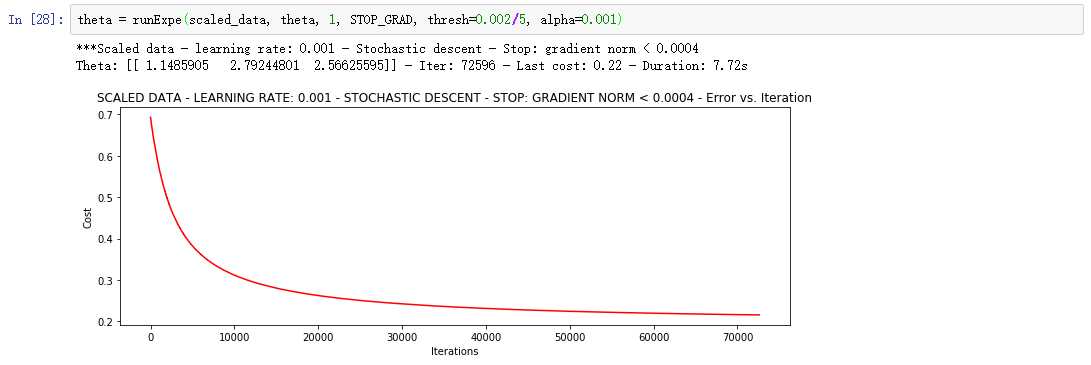
随机梯度下降更快，但是我们需要迭代的次数也需要更多，所以还是用batch的比较合适！

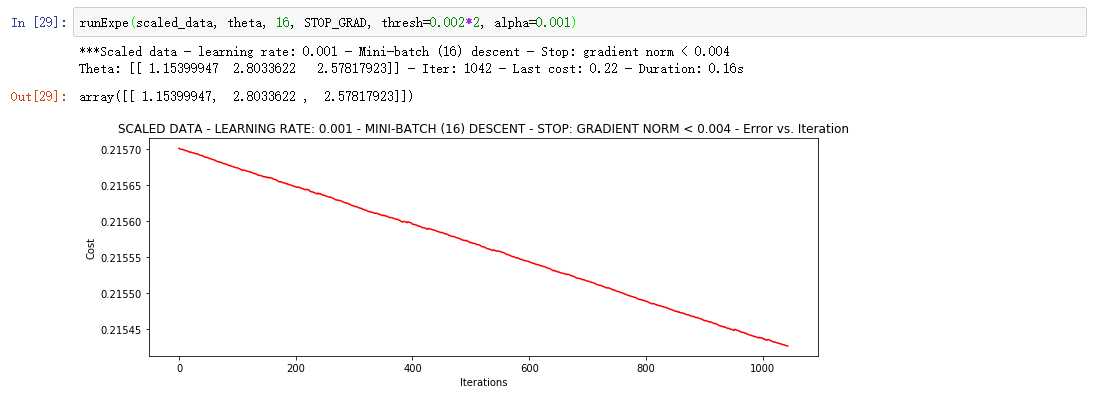
9、精度