【RMQ】 Range Minimum/Maximum Query 范围最值问题
【ST算法】
解决RMQ问题的有效算法
预处理 经过预处理构造出d,预处理时间复杂度 O(nlogn)
运用动态规划的思想 d(i, j) 表示 范围 i ~ i + 2j-1 的最小值则有状态转移方程
d(i, j) = min { d(i, j-1) , d(i + 2j-1 , j-1) }
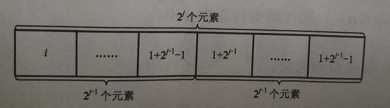
设原数据存储在数组a[] , 则初始状态
d( i , 0 ) = a[ i ]
查询给定区间的最值 时间复杂度O(1)
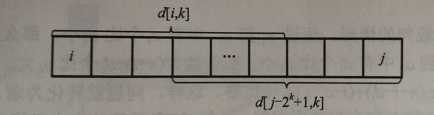
设查询区间为 [ L, R ]
区间长度为 length = R - L + 1 < = 2k (其中k为满足条件的最大整数)
则查询结果为 min { d(L, k) , d( r- 2k + 1 , k ) }
【模板】
#include<iostream> #include<vector> #include<algorithm> using namespace std; /* RMQ-ST算法 区间最小值模板 区间最大值需更改 min() 为 max() by chsobin */ const int maxn = 100; int dp[maxn][maxn]; void RMQ_init(const vector<int>& A){ int n = A.size(); for(int i=0;i<n;++i) dp[i][0] = A[i]; for(int j=1; (1<<j)<=n; j++){ for(int i=0; i+(1<<j)-1<n; i++){ dp[i][j] = min(dp[i][j-1], dp[i + (1<<(j-1))][j-1]); } } } int RMQ(int L, int R){ int k = 0; while( (1<<(k+1)) <= R-L+1 ) k++; return min(dp[L][k], dp[R-(1<<k)+1][k]); } int main() { int a[10] = {1, 5, 8, 7, 2, 6, 1, 9, 3, 4}; vector<int> A(a, a+10); RMQ_init(A); for(int i=0;i<A.size();++i){ cout << A[i] << " "; } cout << endl; while(1){ int L, R; cout << "[L, R]"; cin >> L >> R; cout << RMQ(L, R) << endl; } return 0; }
【题目】
hdu3183

/* 解题思路: 使用RMQ,设原数字长为n,那么除去m个数字后还剩n-m个数字。 (1)因为有n-m个数字,那么在1到m+1位置中最小的那个数字必是结果中的第一个数字,记录其位置为pos (2)然后从这个位置的下个位置pos+1开始到m+2位置的数字中最小的那个数字必定是结果中第二个数字,以此类推下去向后找。 (3)为了保证数字最小,所以要保证高位最小,还要保证数字长度满足条件 */ #include<iostream> #include<cstring> using namespace std; const int maxn = 1010; char a[maxn]; int dp[maxn][11]; char ans[maxn]; int n, m; //自定义 比较规则 int MIN(int i, int j){ return a[i] <= a[j] ? i : j; } //预处理 void init(){ for(int i=0;i<n;++i){ dp[i][0] = i; } for(int j=1;(1<<j)<=n;++j){ for(int i=0;(i + (1<<j) -1 ) < n;++i){ dp[i][j] = MIN(dp[i][j-1], dp[i+ (1<<(j-1)) ][j-1]); } } } //查询 int query(int L, int R){ int k=0; int temp = R-L+1; int sum = 1; while(sum <= temp){ ++k; sum *= 2; } k--; return MIN( dp[L][k], dp[R-(1<<k)+1][k] ); } int main(){ int L = 0; int R = 0; while(scanf("%s%d", a, &m)==2){ int index = 0; L = 0; R = m; n = strlen(a); m = n - m; init(); // // for(int i=0;i<n;++i){ // for(int j=0; (i + (1<<j) -1 ) < n; ++j){ // printf("%c ", a[dp[i][j]]); // } // printf("\n"); // } while(m--){ // cout << "L = "<< L << "R = " << R << endl; L = query(L, R); ans[index++] = a[L]; L++; R++; if(R==n) R = n-1; //保证R不越界 } ans[index] = ‘\0‘; int k = 0; for(;k<index;++k){ //去除前导零 if(ans[k] != ‘0‘) break; } if(k==index) printf("0\n"); else printf("%s\n", ans+k); } return 0; }
【参考】
白书P197

