并查集 - 知乎专栏
这个时候我们就希望重新设计一种数据结构,能够高效的处理这三种操作,分别是
- MAKE-SET(x),创建一个只有元素x的集合,且x不应出现在其他的集合中
- UNION(x, y),将元素x所在集合Sx和元素y所在的集合Sy合并,这里我们假定Sx不等于Sy
- FIND-SET(x),查找元素x所在集合的代表
并查集的具体实现。
对于有根树或者说森林的表示,可以用一个数组parent来实现。
parent[i]记录元素i的父节点的编号,如果节点i本身就是根节点,那么parent[i]就是-1。
MAKE-SET操作就是将parent数组赋值为-1,代码比较简单就不贴了。
UNION操作需要找到两个元素的根,并把其中一个元素的根节点设置为另一个元素的根节点,其实就是调用了两次FIND-SET,代码如下
下面讲一讲并查集的具体实现。对于有根树或者说森林的表示,可以用一个数组parent来实现。parent[i]记录元素i的父节点的编号,如果节点i本身就是根节点,那么parent[i]就是-1。MAKE-SET操作就是将parent数组赋值为-1,代码比较简单就不贴了。UNION操作需要找到两个元素的根,并把其中一个元素的根节点设置为另一个元素的根节点,其实就是调用了两次FIND-SET,代码如下

再来说下FIND-SET这个操作的实现。首先有个很朴素的算法,对父节点递归调用FIND-SET,直到找到根为止。如果父节点是-1,那么返回当前节点,否则递归调用查询父亲的根节点。代码如下
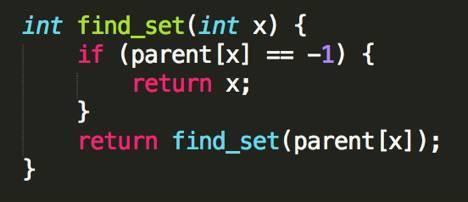
细心的同学会发现,如果我们这棵树很深,那么每次调用FIND-SET可能会需要O(n)的时间,总的复杂度在最坏情况下就是O(nQ)了,那不是更差了吗?
这时候,我们就要引入路径压缩这个概念。什么是路径压缩呢?就是在递归找到根节点的时候,把当前节点到根节点间所有节点的父节点都设置为根节点。举个例子
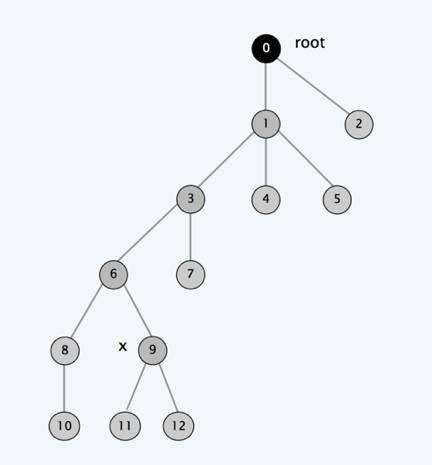
我们来看下图,首先我们有个这样的一棵树,现在要找到元素9所在树的根节点,在找根节点的过程中使用路径压缩,也就是说9到根的路径上的节点9,6,3,1的父节点都设置成为根节点0,所以呢,在FIND-SET(9)之后,树的形态就变成了下面的样子
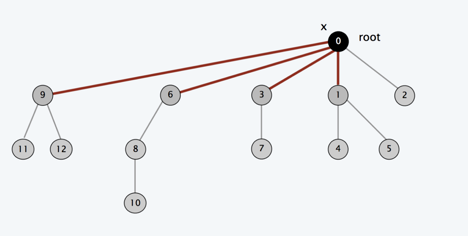
我们可以看到经过路径压缩的节点及其子树到根节点的深度减小了很多,所以在以后的操作中,查找根节点的速度会快很多,平摊下来每次FIND-SET的操作几乎是常数级别的。代码也相当简单,就只多了一句话

刚刚在合并的过程中,并没有提到说到如何选取根,一般情况下两个根节点随意选取一个,如果需要更优的算法,可以按秩合并。除此以外,并查集还能处理带权的情况,因为时间的关系就不在线上分享了。
