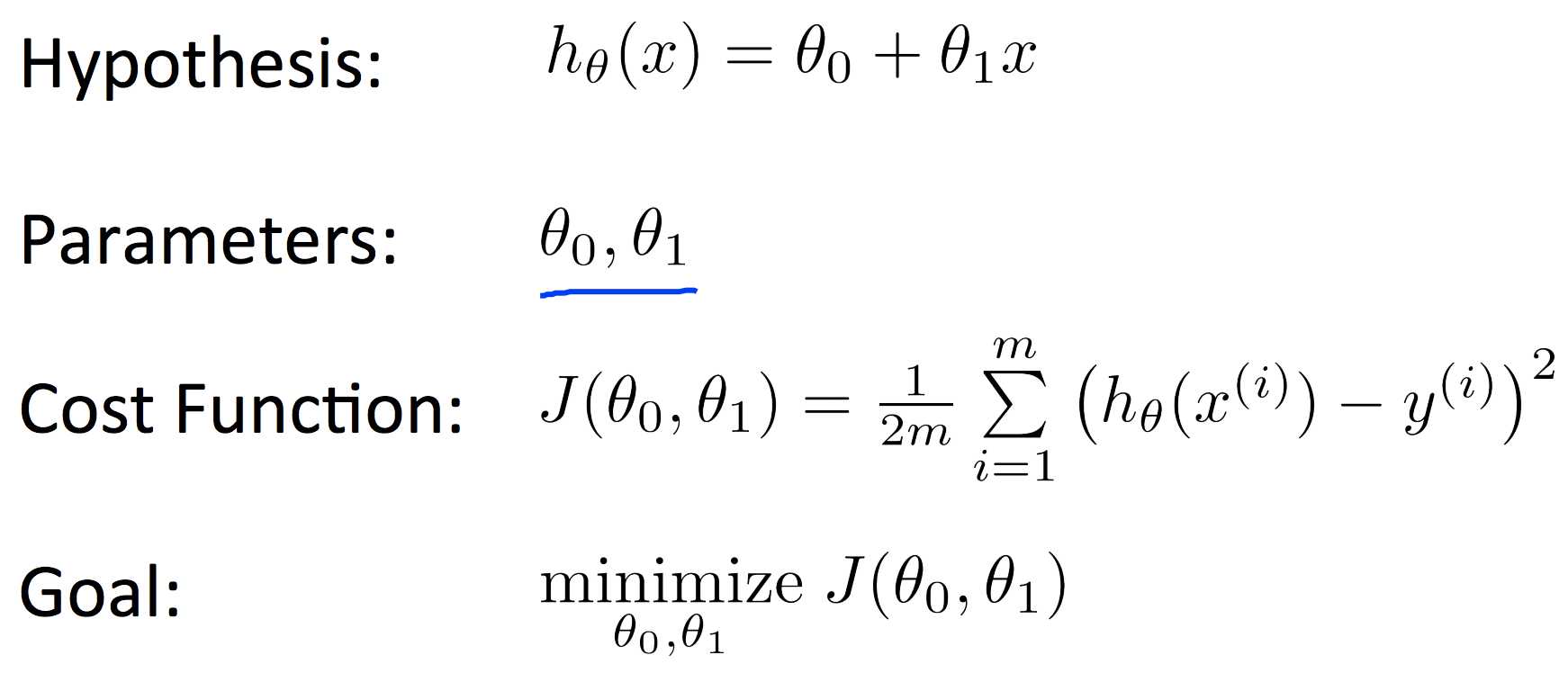Model and Cost Function
Model Representation | 模型表示
To establish notation for future use, we’ll use \(x^{(i)}\) to denote the “input” variables (living area in this example), also called input features, and \(y^{(i)}\) to denote the “output” or target variable that we are trying to predict (price). A pair (\(x^{(i)}\),\(y^{(i)}\)) is called a training example, and the dataset that we’ll be using to learn—a list of m training examples \((x^{(i)}\),\(y^{(i)});i=1,...,m—is\) called a training set. Note that the superscript “(i)” in the notation is simply an index into the training set, and has nothing to do with exponentiation. We will also use X to denote the space of input values, and Y to denote the space of output values. In this example, X = Y = ?.
为了建立未来使用的符号,我们将使用\(x^{(i)}\)来表示“输入”变量(在这个例子中的居住面积),也称为输入要素,\(y^{(i)}\)来表示“输出”或目标变量我们试图预测(价格)。一个对(\(x^{(i)}\),\(y^{(i)}\))被称为一个训练样本,我们将用来学习的数据集 - m个训练样本列表\((x^{(i)}\),\(y^{(i)}); i= 1,...,m-is\) 被称为训练集。注意到符号中的上标“(i)”仅仅是训练集中的一个索引,与取幂无关。我们还将用x来表示输入值的空间,用y来表示输出值的空间。在这个例子中,X = Y =?。
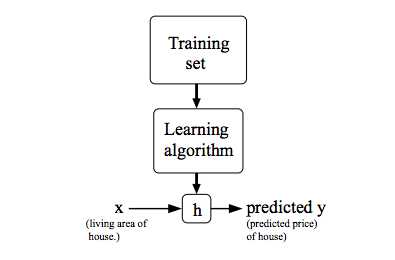
To describe the supervised learning problem slightly more formally, our goal is, given a training set, to learn a function h : X → Y so that h(x) is a “good” predictor for the corresponding value of y. For historical reasons, this function h is called a hypothesis. Seen pictorially, the process is therefore like this:
为了更形式化地描述监督学习问题,我们的目标是在给定训练集的情况下,学习函数\(h:X→Y\),使得\(h(x)\)是\(y\)的相应值的“好”预测器。由于历史原因,这个函数h被称为假设(hypothesis)。看图像,过程是这样的:
When the target variable that we’re trying to predict is continuous, such as in our housing example, we call the learning problem a regression problem. When y can take on only a small number of discrete values (such as if, given the living area, we wanted to predict if a dwelling is a house or an apartment, say), we call it a classification problem.
当我们试图预测的目标变量是连续的时候,比如在我们住房的例子中,我们把学习问题称为回归问题。当y只能接受少量离散值(比如,如果考虑到居住面积,我们想要预测一个住宅是房子还是公寓),我们称之为分类问题。
Cost Function | 代价函数
We can measure the accuracy of our hypothesis function by using a cost function. This takes an average difference (actually a fancier version of an average) of all the results of the hypothesis with inputs from x‘s and the actual output y‘s.
\(J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^{m}(\hat{y_i}?y_i)^2=\frac{1}{2m}\sum_{i=1}^{m}(h_θ(x_i)?y_i)^2\)
To break it apart, it is \(\frac1 2 \bar{x}\) where \(\bar{x}\) is the mean of the squares of $h_θ(x_i)?y_i $, or the difference between the predicted value and the actual value.
This function is otherwise called the "Squared error function", or "Mean squared error". The mean is halved \((\frac1 2)\) as a convenience for the computation of the gradient descent, as the derivative term of the square function will cancel out the \(\frac1 2\) term. The following image summarizes what the cost function does:
我们可以通过使用成本函数来衡量我们的假设函数的准确性。这需要假设的所有结果的平均差异(实际上是一个平均值的更漂亮的版本)与来自x的输入和实际输出y的输入。
\(J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^{m}(\hat{y_i}?y_i)^2=\frac{1}{2m}\sum_{i=1}^{m}(h_θ(x_i)?y_i)^2\)
把它分解开来,其中x是hθ(xi)-yi平方的平均值,或者是预测值与实际值之间的差值。这个函数被称为“平方误差函数”或“均方误差”。由于平方函数的微分项将抵消第12项,所以平均值被减半(12)以方便计算梯度下降。以下图片总结了成本函数的作用: