Introduction
这两天看了一下这篇文章,我就这里分享一下,不过我还是只记录一下跟别人blog上没有,或者自己的想法(ps: 因为有时候翻blog时候发现每篇都一样还是挺烦的= =) 。为了不重复前人的工作,我post一个不小心翻到的博客权值简化(1):三值神经网络(Ternary Weight Networks),整个论文内容及实现都讲的很全面了,可以翻阅一下,我也借鉴一下。
文中主要工作的点在三个方面:
- 增加了网络的表达力(expressive ability)。在{1,0,1}基础上增加了 $\alpha$ 作为scaled factor;
- 压缩模型大小。当然主要是weight的压缩。比起FPWN(full precision weight network)有16~32x的提升,但是BPWN(binary precision weight network)的2x大小(ps:当然在TWN的caffe代码里面,都由float double类型存储,因为这需要在应该上方面来实现);
- 减少计算需求。主要相比于BPWN增多了0,当然这方面也需硬件来获得提升,在该caffe代码里面并没有;
Ternary Quantization
在我的理解看来,文中最核心的内容是:将有约束的并且两变量之间互相依赖的优化问题,逐步拆分最后用具有先验的统计方法来近视解决。
最初的优化问题:
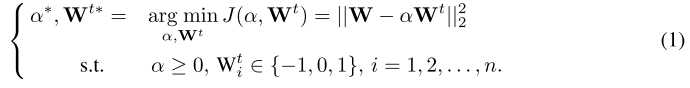
将$W^{t}$的约束具体化为:
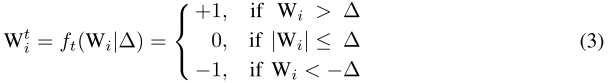
并将其带入公式(1),将$W^{t}$的优化转化为$\Delta^$的优化:
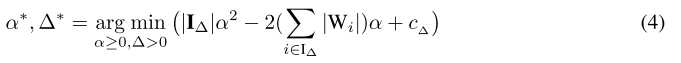
然后对公式(4)中的$\alpha$求偏导,得到:

因为$\alpha$和$\Delta$相互依赖,将(5)代入(4)消去$\alpha$:
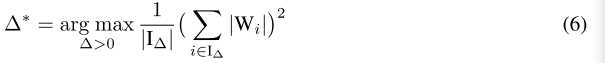
但问题来了,公式(6)依然没法求,而文中就根据先验知识,假设$W_i$服从$N(0,\sigma^2)$分布,近视的$\Delta^$为$0.6\sigma$($0.6\sigma$等于$0.75E(|W|)$)。因此作者采用粗暴的方法,把$\Delta^$设为$\Delta^*\approx0.7E(|W|)\approx\frac{n}{0.7}\sum_{i=1}^n|W_i|$
//caffe-twns
//blob.cpp
template <typename Dtype>
void Blob<Dtype>::set_delta(){
float scale_factor = TERNARY_DELTA * 1.0 / 10; //delta = 0.7
Dtype delta = (Dtype) scale_factor * this->asum_data() / this->count(); // 0.7*(E|W_i|)/num
delta = (delta <= 100) ? delta : 100;
delta = (delta >= -100) ? delta : -100;
this->delta_ = delta;
}
template <typename Dtype>
void Blob<Dtype>::set_delta(Dtype delta){
delta = (delta <= 100) ? delta : 100;
delta = (delta >= -100) ? delta : -100;
this->delta_ = delta;
}Implement
我借用一张图

步骤3~5,其中第5步代码在上面:
template <typename Dtype>
void Blob<Dtype>::ternarize_data(Phase phase){
if(phase == RUN){
// if(DEBUG) print_head();
//LOG(INFO) << "RUN phase...";
// caffe_sleep(3);
return; // do nothing for the running phase
}else if(phase == TRAIN){
//LOG(INFO) << "TRAIN phase ...";
// caffe_sleep(3);
}else{
//LOG(INFO) << "TEST phase ...";
// caffe_sleep(3);
}
// const Dtype delta = 0; // default value;
// const Dtype delta = (Dtype) 0.8 * this->asum_data() / this->count();
this->set_delta(); //defualt 0.7*(E|W_i|)/num or set by user
const Dtype delta = this->get_delta();
Dtype alpha = 1;
if (!data_) { return; }
switch (data_->head()) {
case SyncedMemory::HEAD_AT_CPU:
{
caffe_cpu_ternary<Dtype>(this->count(), delta, this->cpu_data(), this->mutable_cpu_binary()); //quantized weight to ternary
alpha = caffe_cpu_dot(this->count(), this->cpu_binary(), this->cpu_data()); //scale-alpha: (E |W_i|) i belong to I_delta
alpha /= caffe_cpu_dot(this->count(), this->cpu_binary(), this->cpu_binary()); //(1/num_binary)*alpha
caffe_cpu_scale(this->count(), alpha, this->cpu_binary(), this->mutable_cpu_binary());
// this->set_alpha(alpha);
}
return;
case SyncedMemory::HEAD_AT_GPU:
case SyncedMemory::SYNCED:
#ifndef CPU_ONLY
{
caffe_gpu_ternary<Dtype>(this->count(), delta, this->gpu_data(), this->mutable_gpu_binary());
Dtype* pa = new Dtype(0);
caffe_gpu_dot(this->count(), this->gpu_binary(), this->gpu_data(), pa);
Dtype* pb = new Dtype(0);
caffe_gpu_dot(this->count(), this->gpu_binary(), this->gpu_binary(), pb);
alpha = (*pa) / ((*pb) + 1e-6);
this->set_alpha(alpha);
caffe_gpu_scale(this->count(), alpha, this->gpu_binary(), this->mutable_gpu_binary());
// this->set_alpha((Dtype)1);
// LOG(INFO) << "alpha = " << alpha;
// caffe_sleep(3);
}
return;
#else
NO_GPU;
#endif
case SyncedMemory::UNINITIALIZED:
return;
default:
LOG(FATAL) << "Unknown SyncedMemory head state: " << data_->head();
}
}步骤6~7,其中在第6步作者在caffe-twns直接采用传统caffe的方法,而$Z=XW\approx X(\alpha W^t)=(\alpha X)\bigoplus W^t $更偏向与在硬件加速的优化(因为本身在caffe-twns的ternary就采用float或者double,并且用blas或cudnn加速也无法直接跳过0值):
//conv_layer.cpp
template <typename Dtype>
void ConvolutionLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
// const Dtype* weight = this->blobs_[0]->cpu_data();
if(BINARY){
this->blobs_[0]->binarize_data();
}
if(TERNARY){
this->blobs_[0]->ternarize_data(this->phase_); //quantized from blob[0] to ternary sand stored in cpu_binary()
/*
Dtype alpha = (Dtype) this->blobs_[0]->get_alpha();
for(int i=0; i<bottom.size(); i++){
Blob<Dtype>* blob = bottom[i];
caffe_cpu_scale(blob->count(), alpha, blob->cpu_data(), blob->mutable_cpu_data());
}
*/
}
const Dtype* weight = (BINARY || TERNARY) ? this->blobs_[0]->cpu_binary() : this->blobs_[0]->cpu_data();
...
}步骤11~19,weight的Update是在full precision上,而计算gradient则是用ternary weight:
//conv_layer.cpp
template <typename Dtype>
void ConvolutionLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom) {
const Dtype* weight = this->blobs_[0]->cpu_data();
Dtype* weight_diff = this->blobs_[0]->mutable_cpu_diff();
for (int i = 0; i < top.size(); ++i) {
...
if (this->param_propagate_down_[0] || propagate_down[i]) {
for (int n = 0; n < this->num_; ++n) {
// gradient w.r.t. weight. Note that we will accumulate diffs.
if (this->param_propagate_down_[0]) {
this->weight_cpu_gemm(bottom_data + n * this->bottom_dim_,
top_diff + n * this->top_dim_, weight_diff);
}
// gradient w.r.t. bottom data, if necessary.
if (propagate_down[i]) {
this->backward_cpu_gemm(top_diff + n * this->top_dim_, weight,
bottom_diff + n * this->bottom_dim_);
}
}
}
}
}