标签:相对 过程 c++ title 返回结果 精确 算法 计算 优化
毕业半年, 平时工作总是关注业务、架构,而却越来越少关注性能, 也再也没有做过任何涉及算法的工作了希望有时间把这些拉下的东西拾起来,毕竟不论是使用什么语言,从事什么行业,只要是程序员,算法才是真正的基础。
题目来自leetcode,代码语言通常为C/C++,后期可能个别题目会用Golang
万事开头难,但坚持下去其实更难。
(2018.2.3)
题目1:给定和,获取加数
描述: 给定一个整数数组,以及一个整数,已知这个整数是数组内某两个元素的和,现在需要找到,并返回这两个元素的索引,例如:
整数数组:{11, 7, 12, 2}
整数 :9
返回结果:{1, 3}
(假定结果一定存在于给定数组,并且不需要考虑存在多组结果)
题目链接:https://leetcode.com/problems/two-sum/description/
解答:
1、最传统的方法就是挨个查找,判断结果,具体步骤是:
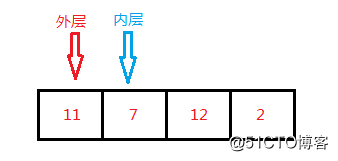
每一趟都从下图第一个元素(11)开始, 固定住第一个元素不变,计算当前元素与其后每个元素的值之和,判断是否等于目标整数
这种方法,最坏的情况下,数组内每一对元素都会被计算一次,因此时间复杂度为O(N * N)
代码:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> ret;
int sz = nums.size();
for(size_t i = 0; i < sz - 1; ++i) {
for(size_t j = i + 1; j < sz; ++j) {
if(nums[i] + nums[j] == target) {
ret.push_back(i);
ret.push_back(j);
return ret;
}
}
}
return ret;
}2、上面的贪婪法可以将步骤分解为两部分,外层循环和内层循环,每当外层循环执行一步,内层循环都需要逐个遍历剩下的元素,执行一趟时间复杂度为O(N)的过程,在整个过程中,外层循环是无法优化的,而内层的循环作为优化,可以考虑用空间换取时间的思路:即事先对整个数组建立索引,使得每一趟的内层循环不再是遍历,而是精确查找,使得算法的时间复杂度由O(N*N)变为O(N*1)
具体步骤是:
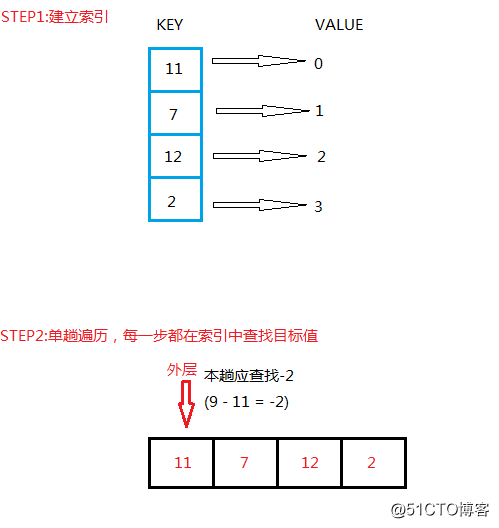
3、建立索引的过程可以分解到外层循环的每一步当中:
一开始无索引,每一步都在索引中查找目标元素,如果没有,则将当前元素存入索引,并迭代至下一步
比较1、2、3方法,
1方法时间复杂度为O(N*N),最低效,
2、3方法整体时间复杂度都是O(N),区别在于 2方法是在一开始就建立了完整的索引,而3方法则是在迭代的过程中逐步建立索引
在悲观的情况下,2、3方法效率是相同的
在乐观的情况下,3方法只需要向索引中存放一个元素,因此相对来说更高效
标签:相对 过程 c++ title 返回结果 精确 算法 计算 优化
原文地址:http://blog.51cto.com/zhweizhi/2068543