【快速傅里叶变换】
参考:从多项式乘法到快速傅里叶变换 by miskcoo
FFT 学习笔记 by Menci
特点:FFT用于O(n log n)解决多项式乘法。
(一)多项式的表示法:
系数表示法:f(x)=a[n-1]*x^(n-1)+...+a[0],称为n-1次多项式。
点值表示法:一个n-1次多项式在复数域中有n个根,即n个(x,y)可以唯一确定一个n-1次多项式。
对于一个多项式,从其系数表示法到其点值表示法的变换称为离散傅里叶变换(DFT),反之称为傅里叶逆变换(IDFT)。
朴素的离散傅里叶变换,枚举实现的复杂度为O(n^2)。
快速傅里叶变换是指以O(n log n)的复杂度实现IDF和IDFT的算法,常用Cooley-Tukey算法。
(二)复数
复数是形如a+bi的数字,当b=0时为实数,b≠0时为虚数,a=0时为纯虚数。
定义一个平面为复平面,那么平面内的每个点(a,b)唯一对应一个复数a+bi,i可以理解为y轴上的单位长度,正如1是x轴上的单位长度。
i的本质是在数轴上定义旋转变换,i是1逆时针旋转90°,那么i^2=-1。
复数相加,遵循平行四边形定则。
复数相乘,模长相乘,幅角相加。
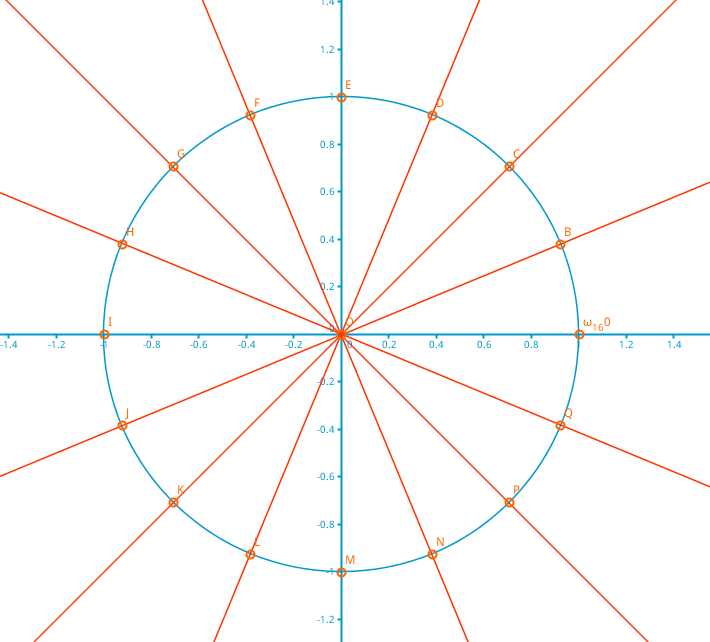
(三)单位根
以圆点为起点,以复平面单位圆的n等分点为终点,作n个向量,设所得幅角为正且最小的向量对应的复数为ω(1,n),即n次单位根。(括号左为上标,右为下标)。
其中B点是单位根ω(1,n),逆时针以此为ω(2,n),ω(3,n)...,ω(n,n)=ω(n,0)=1。
计算公式:ω(k,n)=cos ( 2kπ/n ) + i*sin ( 2kπ/n )

 图片来源:
图片来源: