ng机器学习视频笔记（十一） ——K-均值算法理论

ng机器学习视频笔记（十一）

——K-均值算法理论

（转载请附上本文链接——linhxx）

一、概述

         K均值（K-Means）算法，是一种无监督学习（Unsupervised learning）算法，其核心是聚类（Clustering），即把一组输入，通过K均值算法进行分类，输出分类结果。

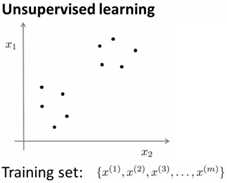
         由于K均值算法是无监督学习算法，故这里输入的样本和之前不同了，输入的样本只有样本本身，没有对应的样本分类结果，即这里的输入的仅仅是{x⁽¹⁾,x⁽²⁾,…x^(m)}，每个x没有对应的分类结果y⁽ⁱ⁾，需要我们用算法去得到每个x对应的y。

         K均值算法，常用的场景包括市场分析中分析不同用户属于哪类用户、社交网络中分析用户之间的关系、计算机集群设计分析、星系形成过程分析等。

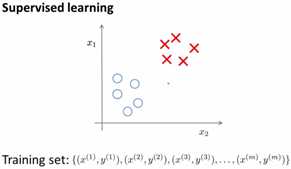
         无监督学习和监督学习输入的区别如下：

二、算法基本步骤

1、前提

         现假设数据点有m个，需要有K个分类。

2、步骤

         1）随机初始化K个点，作为K个分类的中心点，每个中心点称为聚类中心（cluster centroid），也成为簇。下图是K=2时，随机选2个簇。

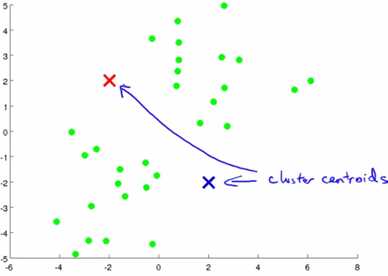
         2）根据K个中心点，遍历所有样本，分别计算每个样本到每个中心点的距离，把样本分到最近的举例。

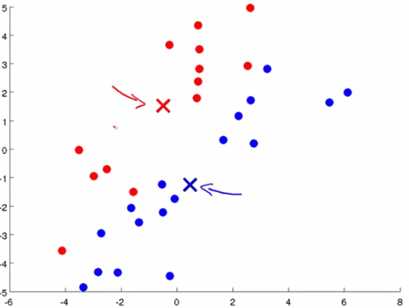
3）分类完成后，根据分类完成的结果，计算在每个分类中的样本的平均值，把聚类中心移动到这些平均值中。

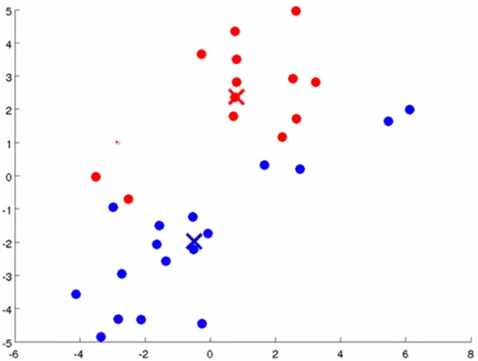
         4）重复步骤2、步骤3，直到聚类中心稳定。

         综上，步骤如下：

3、特殊情况

         当随机选到的某个聚类中心，如果在一次分类中，没有一个样本被分到这个聚类中心，则如果有固定的分类结果数量要求，则需要重新随机选择初始聚类中心，重新进行K均值计算。为了速度较快，可以存储这些没有任何分类结果的点，在随机初始聚类中心时，避免选到这些点。

三、代价函数

1、符号

         在K均值算法中，K（大写）表示分类结果数量（K=3表示样本要分成3类），k（小写）表示第k个聚类中心， C⁽ⁱ⁾表示样本x⁽ⁱ⁾所属的聚类中心编号，μ_k表示第k个聚类中心的位置，μ_C⁽ⁱ⁾表示x⁽ⁱ⁾所属的聚类中心位置。

         例如，x⁽ⁱ⁾被分类到第5个聚类中心，则C⁽ⁱ⁾=5，μ_C⁽ⁱ⁾= μ₅。

2、代价函数

         K均值算法的代价函数，又称为K均值算法的dispulsion函数，公式如下：

         可以证明，对于代价函数的公式：

1）K均值算法的第二步（即选好聚类中心后，需要把每个样本分类到对应的聚类中心），对于优化代价函数而言，相当于固定μ的值，来计算J(c)的最优情况。

2）算法的第三步（即通过计算每个聚类的样本均值重新选定聚类中心），对于优化代价函数而言，相当于通过μ的优化来确定最优的J。

四、初始化聚类中心

1、前提

         随机初始化聚类中心，前提是要求总的分类数量K小于样本数量m，否则分类没有意义。

2、步骤

         1）在m个样本中，随机选出K个样本。

         2）令μ₁、μ₂…μ_k等于这K个样本。

         简单来说，即在样本中随机初始化聚类中心，而不是漫无目的的在整个坐标系中来随机。

3、存在问题——局部最小值

         K均值算法的代价函数，也存在局部最优解（极小值）的情况，这个对于K均值算法来说非常不好，如下图所示：

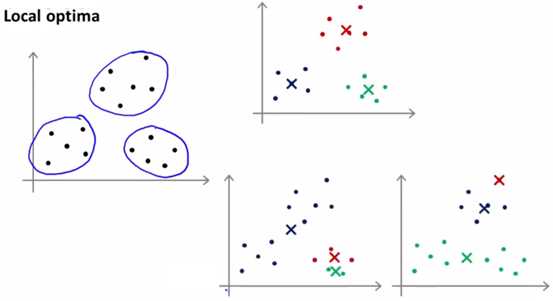
         上图左边是待分类的样本，右边上方是根据日常经验来说应该被分类的样子，而右边下面两个分类结果，都是出现局部极小值的结果。即一开始随机初始化的时候，有两个初始化点都被初始化在本来应该被分在一个类的“地盘”，这就导致后面优化的时候，会不断的按这个本来就错误的方式来优化。

4、解决方案

         为了避免局部最小值的情况，可以多次进行K均值算法的运算。每次分类稳定后，记录该分类的方式，以及该分类方式下最终的代价函数（即每个点到聚类中心点的距离的平方和），然后取这些分类结果中，带价值最小的分类方式，作为最终的分类方式。

         如下图所示：

         通常而言，当执行K均值算法超过50次，则最终一般可以避免局部最优解的错误分类结果。

         另外，局部最优解，一般只在K比较小（K在2~10左右）的时候容易发生，当K非常大时，通常不会发生局部最优解，或者说这种局部最优解和最佳解的差距也不是非常大，可以接受。

五、确定分类数量K

         在不确定要分几类时，需要确定分类数量K。

1、方法一：肘部法则

         肘部法则（Elbow Method），即通过改变K值，描绘出K和代价函数J的图像，并且确定在某个K时，代价函数降低的最多（图像类似人类的肘部），则取这个K作为应当的分类结果，如下图的左边的图像所示。

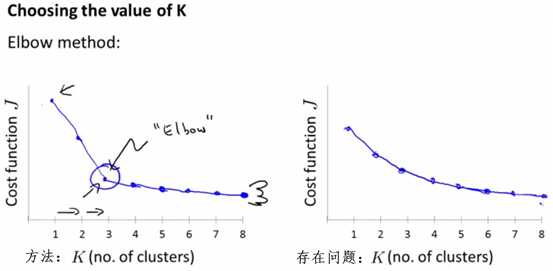
         但是肘部法则存在问题，如上图的右图所示，当K-J的图像，不存在一个剧烈的降低点（从图像中无法明确哪个K是肘部），而是比较平缓的降低，则此时无法通过肘部法则来明确选择哪个K是最佳的。

2、方法二

         当肘部法则无法确定K时，更通用的方式，是分析当前的业务场景，并且通过业务场景，来明确所需要的分类结果。

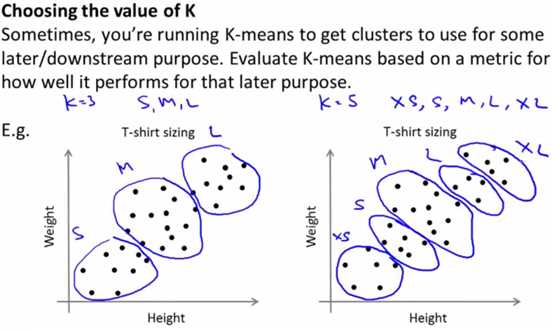
         例如下图是根据 身高和体重的人群分布，需要确定设计的T恤衫的尺寸。例如可以分为3类（左图）、5类（右图），分类都是合理的。

         此时，就需要通过认为的经验分析，明确应该选哪种K作为最佳分类。

六、小结

         K均值算法，作为无监督学习方法，其思想和分析方式，和监督学习算法有比较大的不同。应当明确，监督学习是提前告知分类结果，而无监督学习并没有提前告知分类结果，他们是有不同的业务场景，因此必然设计思想完全不同。

——written by linhxx

更多最新文章，欢迎关注微信公众号“决胜机器学习”，或扫描右边二维码。