前面的文章对线性回归做了一个小结,文章在这: 线性回归原理小结。里面对线程回归的正则化也做了一个初步的介绍。提到了线程回归的L2正则化-Ridge回归,以及线程回归的L1正则化-Lasso回归。但是对于Lasso回归的解法没有提及,本文是对该文的补充和扩展。以下都用矩阵法表示,如果对于矩阵分析不熟悉,推荐学习张贤达的《矩阵分析与应用》。
1. 回顾线性回归
首先我们简要回归下线性回归的一般形式:
hθ(X)=Xθhθ(X)=Xθ
需要极小化的损失函数是:
J(θ)=12(Xθ?Y)T(Xθ?Y)J(θ)=12(Xθ?Y)T(Xθ?Y)
如果用梯度下降法求解,则每一轮θθ迭代的表达式是:
θ=θ?αXT(Xθ?Y)θ=θ?αXT(Xθ?Y)
其中αα为步长。
如果用最小二乘法,则θθ的结果是:
θ=(XTX)?1XTYθ=(XTX)?1XTY
2. 回顾Ridge回归
由于直接套用线性回归可能产生过拟合,我们需要加入正则化项,如果加入的是L2正则化项,就是Ridge回归,有时也翻译为脊回归。它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项,和一个调节线性回归项和正则化项权重的系数αα。损失函数表达式如下:
J(θ)=12(Xθ?Y)T(Xθ?Y)+12α||θ||22J(θ)=12(Xθ?Y)T(Xθ?Y)+12α||θ||22
其中αα为常数系数,需要进行调优。||θ||2||θ||2为L2范数。
Ridge回归的解法和一般线性回归大同小异。如果采用梯度下降法,则每一轮θθ迭代的表达式是:
θ=θ?(βXT(Xθ?Y)+αθ)θ=θ?(βXT(Xθ?Y)+αθ)
其中ββ为步长。
如果用最小二乘法,则θθ的结果是:
θ=(XTX+αE)?1XTYθ=(XTX+αE)?1XTY
其中E为单位矩阵。
模型变量多的缺点呢?有,这就是下面说的Lasso回归。
3. 初识Lasso回归
Lasso回归有时也叫做线性回归的L1正则化,和Ridge回归的主要区别就是在正则化项,Ridge回归用的是L2正则化,而Lasso回归用的是L1正则化。Lasso回归的损失函数表达式如下:
J(θ)=12n(Xθ?Y)T(Xθ?Y)+α||θ||1J(θ)=12n(Xθ?Y)T(Xθ?Y)+α||θ||1
其中n为样本个数,αα为常数系数,需要进行调优。||θ||1||θ||1为L1范数。
4. 用坐标轴下降法求解Lasso回归
坐标轴下降法顾名思义,是沿着坐标轴的方向去下降,这和梯度下降不同。梯度下降是沿着梯度的负方向下降。不过梯度下降和坐标轴下降的共性就都是迭代法,通过启发式的方式一步步迭代求解函数的最小值。
坐标轴下降法的数学依据主要是这个结论(此处不做证明):一个可微的凸函数J(θ)J(θ), 其中θθ是nx1的向量,即有n个维度。如果在某一点θˉˉˉθˉ,使得J(θ)J(θ)在每一个坐标轴θˉˉˉiθˉi(i = 1,2,...n)上都是最小值,那么J(θˉˉˉi)J(θˉi)就是一个全局的最小值。
于是我们的优化目标就是在θθ的n个坐标轴上(或者说向量的方向上)对损失函数做迭代的下降,当所有的坐标轴上的θiθi(i = 1,2,...n)都达到收敛时,我们的损失函数最小,此时的θθ即为我们要求的结果。
下面我们看看具体的算法过程:
1. 首先,我们把θθ向量随机取一个初值。记为θ(0)θ(0) ,上面的括号里面的数字代表我们迭代的轮数,当前初始轮数为0.
2. 对于第k轮的迭代。我们从θ(k)1θ1(k)开始,到θ(k)nθn(k)为止,依次求θ(k)iθi(k)。θ(k)iθi(k)的表达式如下:
θ(k)i∈argminθiJ(θ(k)1,θ(k)2,...θ(k)i?1,θi,θ(k?1)i+1,...,θ(k?1)n)θi(k)∈argmin?θiJ(θ1(k),θ2(k),...θi?1(k),θi,θi+1(k?1),...,θn(k?1))
也就是说θ(k)iθi(k)是使J(θ(k)1,θ(k)2,...θ(k)i?1,θi,θ(k?1)i+1,...,θ(k?1)n)J(θ1(k),θ2(k),...θi?1(k),θi,θi+1(k?1),...,θn(k?1))最小化时候的θiθi的值。此时J(θ)J(θ)只有θ(k)iθi(k)是变量,其余均为常量,因此最小值容易通过求导求得。
如果上面这个式子不好理解,我们具体一点,在第k轮,θθ向量的n个维度的迭代式如下:
θ(k)1∈argminθ1J(θ1,θ(k?1)2,...,θ(k?1)n)θ1(k)∈argmin?θ1J(θ1,θ2(k?1),...,θn(k?1))
θ(k)2∈argminθ2J(θ(k)1,θ2,θ(k?1)3...,θ(k?1)n)θ2(k)∈argmin?θ2J(θ1(k),θ2,θ3(k?1)...,θn(k?1))
...
θ(k)n∈argminθnJ(θ(k)1,θ(k)2,...,θ(k)n?1,θn)θn(k)∈argmin?θnJ(θ1(k),θ2(k),...,θn?1(k),θn)
3. 检查θ(k)θ(k)向量和θ(k?1)θ(k?1)向量在各个维度上的变化情况,如果在所有维度上变化都足够小,那么θ(k)θ(k)即为最终结果,否则转入2,继续第k+1轮的迭代。
以上就是坐标轴下降法的求极值过程,可以和梯度下降做一个比较:
5. 用最小角回归法求解Lasso回归
第四节介绍了坐标轴下降法求解Lasso回归的方法,此处再介绍另一种常用方法, 最小角回归法(Least Angle Regression, LARS)。
在介绍最小角回归前,我们先看看两个预备算法,好吧,这个算法真没有那么好讲。
5.1 前向选择(Forward Selection)算法
第一个预备算法是前向选择(Forward Selection)算法。
前向选择算法的原理是是一种典型的贪心算法。要解决的问题是对于:
Y=XθY=Xθ这样的线性关系,如何求解系数向量θθ的问题。其中YY为 mx1的向量,XX为mxn的矩阵,θθ为nx1的向量。m为样本数量,n为特征维度。
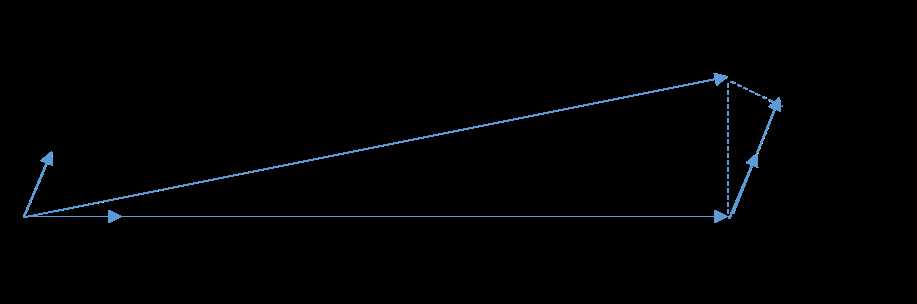
把 矩阵XX看做n个mx1的向量XiXi(i=1,2,...n),在YY的XX变量XiXi(i =1,2,...m)中,选择和目标YY最为接近(余弦距离最大)的一个变量XkXk,用XkXk来逼近YY,得到下式:
Yˉˉˉˉ=XkθkYˉ=Xkθk
5.2 前向梯度(Forward Stagewise)算法
第二个预备算法是前向梯度(Forward Stagewise)算法。
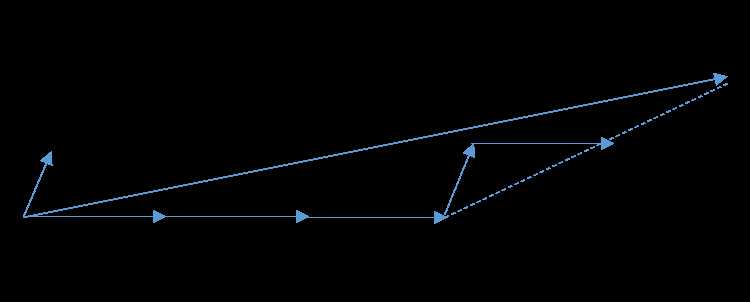
前向梯度算法和前向选择算法有类似的地方,也是在YY的XX变量XiXi(i =1,2,...n)中,选择和目标YY最为接近(余弦距离最大)的一个变量XkXk,用XkXk来逼近YY,但是前向梯度算法不是粗暴的用投影,而是每次在最为接近的自变量XtXt的方向移动一小步,然后再看残差YyesYyes和哪个XiXi(i =1,2,...n)最为接近。此时我们也不会把XtXt 去除,因为我们只是前进了一小步,有可能下面最接近的自变量还是XtXt。如此进行下去,直到残差YyesYyes减小到足够小,算法停止。
有没有折中的办法可以综合前向梯度算法和前向选择算法的优点,做一个折中呢?有!这就是终于要出场的最小角回归法。
5.3 最小角回归(Least Angle Regression, LARS)算法
好吧,最小角回归(Least Angle Regression, LARS)算法终于出场了。最小角回归法对前向梯度算法和前向选择算法做了折中,保留了前向梯度算法一定程度的精确性,同时简化了前向梯度算法一步步迭代的过程。具体算法是这样的:
首先,还是找到与因变量YY最接近或者相关度最高的自变量XkXk,使用类似于前向梯度算法中的残差计算方法,得到新的目标YyesYyes,此时不用和前向梯度算法一样小步小步的走。而是直接向前走直到出现一个XtXt,使得XtXt和YyesYyes的相关度和XkXk与YyesYyes的相关度是一样的,此时残差YyesYyes就在XtXt和XkXk的角平分线方向上,此时我们开始沿着这个残差角平分线走,直到出现第三个特征XpXp和YyesYyes的相关度足够大的时候,即XpXp到当前残差YyesYyes的相关度和θtθt,θkθk与YyesYyes的一样。将其也叫入到YY的逼近特征集合中,并用YY的逼近特征集合的共同角分线,作为新的逼近方向。以此循环,直到YyesYyes足够的小,或者说所有的变量都已经取完了,算法停止。此时对应的系数θθ即为最终结果。
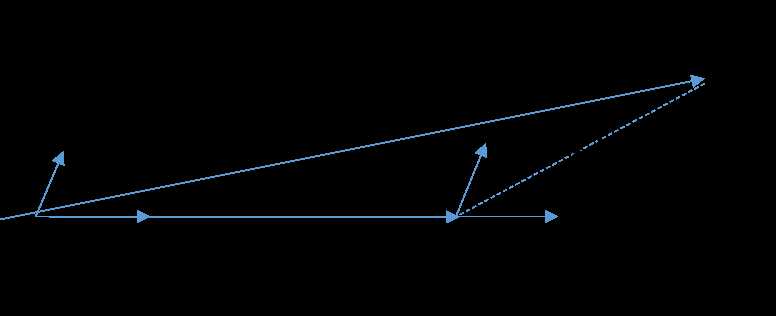
当θθ只有2维时,例子如上图,和YY最接近的是X1X1,首先在X1X1上面走一段距离,一直到残差在X1X1和X2X2的角平分线上,此时沿着角平分线走,直到残差最够小时停止,此时对应的系数ββ即为最终结果。此处θθ计算设计较多矩阵运算,这里不讨论。
最小角回归法是一个适用于高维数据的回归算法,其主要的优点有:
1)特别适合于特征维度n 远高于样本数m的情况。
2)算法的最坏计算复杂度和最小二乘法类似,但是其计算速度几乎和前向选择算法一样
3)可以产生分段线性结果的完整路径,这在模型的交叉验证中极为有用
主要的缺点是:
由于LARS的迭代方向是根据目标的残差而定,所以该算法对样本的噪声极为敏感。
6. 总结
Lasso回归是在ridge回归的基础上发展起来的,如果模型的特征非常多,需要压缩,那么Lasso回归是很好的选择。一般的情况下,普通的线性回归模型就够了。
另外,本文对最小角回归法怎么求具体的θθ参数值没有提及,仅仅涉及了原理,如果对具体的算计推导有兴趣,可以参考Bradley Efron的论文《Least Angle Regression》,网上很容易找到。
