监督学习
对于一个房价预测系统,给出房间的面积和价格,以面积和价格作坐标轴,绘出各个点。
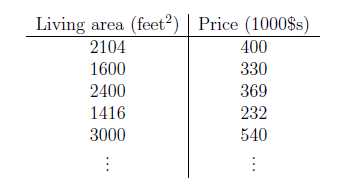
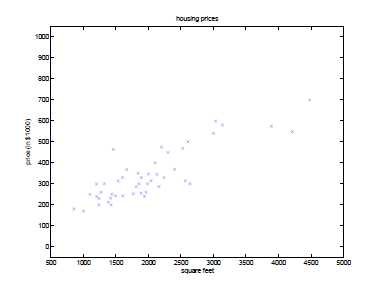
定义符号:
\(x_{(i)}\)表示一个输入特征\(x\)。
\(y_{(i)}\)表示一个输出目标\(y\)。
\((x_{(i)},y_{(i)})\)表示一个训练样本。
\(\left\{(x_{(i)},y_{(i)});i=1,\dots,m\right\}\)代表m个样本,也称为训练集。
上标\((i)\)代表样本在训练集中的索引。
\(\mathcal{X}\)代表输入值的空间,\(\mathcal{Y}\)代表输出值的空间。\(\mathcal{X}=\mathcal{Y}=\mathbb{R}\)
监督学习的目标,就是给定一个训练集,学习一个函数\(h\):\(\mathcal{X} \mapsto \mathcal{Y}\)。\(h(x)\)是对于y的对应值的一个“好”的预测。函数\(h\)被称为hypothesis函数(假设函数)
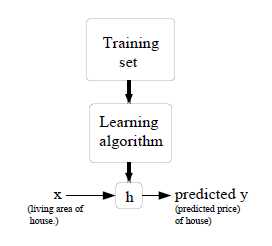
如果我们预测的目标值是连续的,那么,这种问题被称为回归问题,如果\(y\)只是一个离散的小数字,那么,这种问题叫做分类问题。
线性回归
假设房价不仅与面积有关,还与卧室数有关,如下:
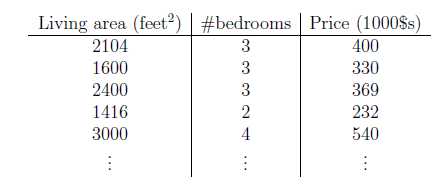
这时候的\(x\)是一个2维向量\(\in \mathbb{R^2}\)。其中\(x_1^{(i)}\)表示第\(i\)个样本的房子面积,\(x_2^{(i)}\)表示第\(i\)个样本的房子卧室数。
现在我们决定将y近似为x的线性函数,公式如下:
\[h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2\]
\(\theta_i\)是线性函数空间从\(\mathcal{X}\)到\(\mathcal{Y}\)映射的参数(权重)。把公式简化:
\[h(x)=\sum_{i=0}^n \theta_ix_i=\theta^Tx\]
其中\(x_0\)=1,因此\(x_0\theta_0=\theta_0\)是截距。\(\theta\)和\(x\)都是向量,\(n\)是输入值的数量(不包括\(x_0\))
为了学习参数\(\theta\),我们定义损失函数:
\[J(\theta)=\frac{1}{2}\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})^2\]
上式产生一个普通最小二乘法回归模型。
1 LMS(least mean squares)算法
为了选择一个\(\theta\)来使\(J(\theta)\)最小化,先随机对\(\theta\)设置随机值,然后使用一个搜索算法来不断更新\(\theta\)以使\(\theta\)收敛到希望达到的最小化\(J(\theta)\)的值。这里用梯度下降算法,首先初始化\(\theta\),然后不断执行更新:
\[\theta_j:=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J(\theta)\]
\(\alpha\)是学习率(learning rate)。上式同时对所有的\(j = (0,\dots,n)\)值执行。
首先求一个样本\((x,y)\)的偏导数,后面再求总和:
\[\begin{align} \frac{\partial}{\partial \theta_j}J(\theta)&=\frac{\partial}{\partial \theta_j}\frac{1}{2}(h_{\theta}(x)-y)^2\\&=2*\frac{1}{2}(h_{\theta}(x)-y)*\frac{\partial}{\partial \theta_j}(h_{\theta}(x)-y)\\&=(h_{\theta}(x)-y)*\frac{\partial}{\partial \theta_j}\left(\sum_{i=0}^n \theta_ix_i-y\right)\\&=(h_{\theta}(x)-y)x_j\\\end{align}\]
对于单个样本,更新规则(LMS更新规则或Widrow-Hoff学习规则):
\[\theta_j:=\theta_j+\alpha\left(y^{(i)}-h_{\theta}(x^{(i)})\right)x_j^{(i)}\]
上式中更新规则与\((y_{(i)}-h_{\theta(x_{(i)})})\)误差项成正比,如果预测结果与输出值相差小,则\(\theta\)变化小;反之,则变化大。
批量梯度下降:
对于所有的\(\theta\)值重复计算直至收敛\(\{\)
\[\theta_j:=\theta_j+\alpha \begin{matrix} \sum_{i=1}^m (y_{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)} \end{matrix}\]
\(\}\)
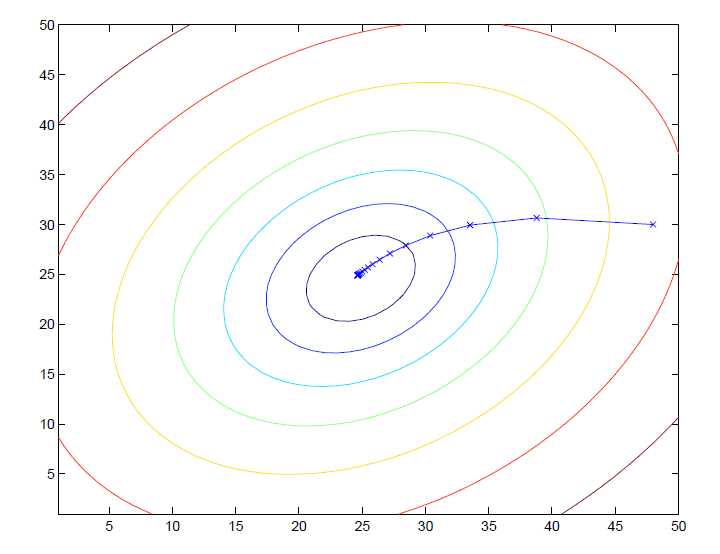
计算出\(\theta_1\)和\(\theta_2\)后,代入\(h_{\theta}(x)\)中作为\(x\)的函数,绘制的图如下:
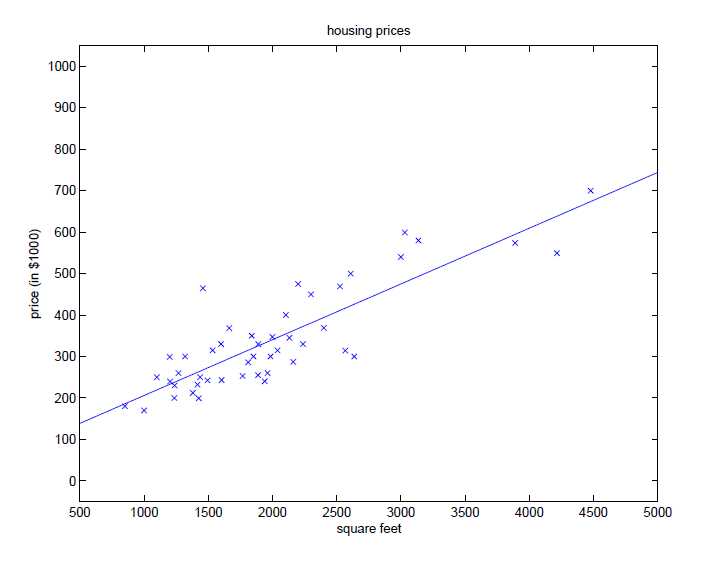
随机梯度下降(增量梯度下降):
\[\begin{align} Loop \{ \\& for\;i=1\;to\;m \{ \\&& \theta_j:=\theta_j+\alpha(y_{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)}&(for every j) \\&\} \\\} \\\end{align}\]
每次只对一个样本进行更新。
随机梯度下降通常比批量梯度下降要好,因为批量梯度下降是每次更新整个训练集,十分耗时。
2 正态方程
梯度下降是最小化\(J\)的方法之一,除此之外,正态方程也能最小化\(J\)。通过对\(\theta_j\)求导,然后让它等于0,以使得\(J\)最小化。
2.1矩阵导数
函数\(f\):\(\mathbb{R}^{m\times n} \mapsto \mathbb{R}\)映射,表示从\((m,n)\)矩阵到一个实数的函数。我们定义函数\(f\)对\(A\)求导:
\[\nabla_Af(A) = \begin{bmatrix} \frac{\partial f}{\partial A_{11}} & \dots & \frac{\partial f}{\partial A_{1n}} \\vdots & \ddots & \vdots \\frac{\partial f}{\partial A_{m1}} & \dots & \frac{\partial f}{\partial A_{mn}} \\end{bmatrix}\]
\(\nabla_Af(A)\)是一个\((m,n)\)的矩阵,每个元素是\(\frac{\partial f}{\partial A_{ij}}\),比如,如果
\(A=\begin{bmatrix} A_{11}&A_{12}\\ A_{21}&A_{22}\\ \end{bmatrix}\)是一个\(2\times 2\)矩阵。函数$f:\mathbb{R}^{2 \times 2} \mapsto \mathbb{R} $:
\[f(A) = \frac{3}{2}A_{11}+5A_{12}^2+A_{21}A_{22}\]
因此,函数\(f\)对\(A\)求导:
\[\nabla_Af(A) = \begin{bmatrix} \frac{3}{2}&10A_{12}\A_{22}&A_{21}\\end{bmatrix}\]
迹运算
对于一个\(n\times n\)的矩阵求迹,公式:
\[trA=\sum_{i=1}^n A_{ii}\]
如果\(a\)是一个实数(例如一个\(1\times 1\)的矩阵),那么\(tr\,a = a\)。
对于两个矩阵\(A\)和\(B\),迹运算有:
\[trAB=trBA\]
多个矩阵:
\[trABC=trCAB=trBCA\]
\[trABCD=trDABC=trCDAB=trBCDA\]
对于两个相等方阵\(A\)和\(B\),还有一个实数\(A\),有公式:
\[trA=trA^T\]
\[tr(A+B)=trA+trB\]
\[traA=atrA\]
矩阵导数公式:
\[\nabla_A trAB = B^T\qquad \qquad \qquad \qquad(1)\]
\[\nabla_{A^T} f(A) = (\nabla_Af(A))^T \qquad \qquad \qquad(2)\]
\[\nabla_A trABA^TC = CAB + C^TAB^T \qquad \qquad \qquad(3)\]
\[\nabla_A |A| = |A|(A^{-1})^T \qquad \qquad \qquad(4)\]
令\(A\in \mathbb{R}^{n\times m}\),\(B\in \mathbb{R}^{m\times n}\)求证公式(1)\(\nabla_A trAB = B^T\):
\[A=\begin{bmatrix} A_{11} & \dots & A_{1m}\\vdots & \ddots & \vdots\A_{n1} & \dots & A_{nm} \end{bmatrix}\]
\[B=\begin{bmatrix} B_{11} & \dots & B_{1n}\\vdots & \ddots & \vdots\B_{m1} & \dots & B_{mn} \end{bmatrix}\]
\[\begin{align} \nabla_A trAB&= \nabla_A tr\left(\begin{bmatrix} A_{11} & \dots & A_{1m}\\vdots & \ddots & \vdots\A_{n1} & \dots & A_{nm} \end{bmatrix} \times \begin{bmatrix} B_{11} & \dots & B_{1n}\\vdots & \ddots & \vdots\B_{m1} & \dots & B_{mn} \end{bmatrix}\right)\&=\nabla_A tr\left(\begin{bmatrix} A_{11}B_{11}+A{12}B_{21}+\dots+A_{1m}B_{m1}&\dots&A_{11}B_{1k}+A_{12}B_{2k}+\dots+A_{1m}B_{mk}&\dots&A_{11}B_{1n}+A{12}B_{2n}+\dots+A_{1m}B_{mn}\\vdots&\vdots&\vdots&\vdots&\vdots\A_{k1}B_{11}+A{k2}B_{21}+\dots+A_{km}B_{m1}&\dots&A_{k1}B_{1k}+A_{k2}B_{2k}+\dots+A_{km}B_{mk}&\dots&A_{k1}B_{1n}+A{k2}B_{2n}+\dots+A_{km}B_{mn}\\vdots&\vdots&\vdots&\vdots&\vdots\A_{n1}B_{11}+A{n2}B_{21}+\dots+A_{nm}B_{m1}&\dots&A_{n1}B_{1k}+A_{n2}B_{2k}+\dots+A_{nm}B_{mk}&\dots&A_{n1}B_{1n}+A{n2}B_{2n}+\dots+A_{nm}B_{mn} \end{bmatrix}\right)\&=\nabla_A \left(A_{11}B_{11}+A{12}B_{21}+\dots+A_{1m}B_{m1}+A_{k1}B_{1k}+A_{k2}B_{2k}+\dots+A_{km}B_{mk}+A_{n1}B_{1n}+A{n2}B_{2n}+\dots+A_{nm}B_{mn}\right)\&=\begin{bmatrix} B_{11}&\dots&b_{m1}\\vdots&\ddots&\vdots\B_{1n}&\dots&B_{mn} \end{bmatrix}\&=B^T \\\end{align}\]
方程(4)可以利用矩阵逆的伴随表示来得到。
2.2 最小二乘回归
获取一个训练集,定义决策矩阵\(X\)是\((m\times n)\)(如果包含截距项,则是\((m\times n+1)\)):
\[X=\begin{bmatrix}
—(x^{(1)})^T—\—(x^{(2)})^T—\—\vdots—\—(x^{(m)})^T—
\end{bmatrix}\]
令\(\overrightarrow y\)作为一个m维向量,包含训练集的所有目标值。
\[\overrightarrow y=\begin{bmatrix} —(y^{(1)})—\—(y^{(2)})—\—\vdots—\—(y^{(m)})— \end{bmatrix}\]
因为\(h_{\theta}(x^{(i)})=(x^{(i)})^T\theta\),\(\theta\)是一个\((n\times 1)\)向量,所以有:
\[\begin{align} X\theta-\overrightarrow y &= \begin{bmatrix} —(x^{(1)})^T\theta—\—(x^{(2)})^T\theta—\—\vdots—\—(x^{(m)})^T\theta— \end{bmatrix} - \begin{bmatrix} —(y^{(1)})—\—(y^{(2)})—\—\vdots—\—(y^{(m)})— \end{bmatrix}\&=\begin{bmatrix} h_{\theta}(x^{(1)})-(y^{(1)})\h_{\theta}(x^{(2)})-(y^{(2)})\\vdots\h_{\theta}(x^{(m)})-y^{(m)}) \end{bmatrix} \\\end{align}\]
对于一个向量\(z\),我们有\(z^Tz=\begin{matrix} \sum_i z_i^2 \end{matrix}\):
\[\begin{align} \frac{1}{2}(X\theta-\overrightarrow y)^T(X\theta-\overrightarrow y)&=\frac{1}{2} \sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})^2 \\&=J(\theta) \\\end{align}\]
在对\(\theta\)求导前,首先根据方程(2)和方程(3),得:
\[\nabla_{A^T}trABA^TC = B^TA^TC^T + BA^TC\qquad \qquad \qquad \qquad(5)\]
因此:
\[\begin{align} \nabla_{\theta}J(\theta) &=\nabla_{\theta}\frac{1}{2}(X\theta-\overrightarrow y)^T(X\theta-\overrightarrow y)\&=\frac{1}{2}\nabla_{\theta}(\theta^TX^TX\theta-\theta^TX^T\overrightarrow y-\overrightarrow y^TX\theta+\overrightarrow y^T\overrightarrow y)\&=\frac{1}{2}\nabla_{\theta}tr(\theta^TX^TX\theta-\theta^TX^T\overrightarrow y-\overrightarrow y^TX\theta+\overrightarrow y^T\overrightarrow y)\&=\frac{1}{2}\nabla_{\theta}(tr\theta^TX^TX\theta-2tr\overrightarrow y^TX\theta)\&=\frac{1}{2}(X^TX\theta+X^TX\theta-2X^T\overrightarrow y)\&=X^TX\theta-X^T\overrightarrow y \end{align}\]
在第三步,因为\(\theta=(n\times 1),X=(m\times n)\),所以\(\theta^TX^TX\theta-\theta^TX^T\overrightarrow y-\overrightarrow y^TX\theta+\overrightarrow y^T\overrightarrow y\)计算后得出是一个\((1\times 1)\)矩阵,即一个实数,根据\(tr\,a = a\)可推导出第2步和第3步。第5步用方程(5),通过使\(A^T=\theta,B=B^T=X^TX和C=I还有方程(1)\)得出。要使\(J\)最小化,则令\(\nabla_{\theta}J(\theta)\)为0,得出:
\[X^TX\theta=X^T\overrightarrow y\]
所以,要使\(J\)最小化,则需要令:
\[\theta=(X^TX)^{-1}X^T\overrightarrow y\]
3 概率解释
为什么在处理一个回归问题的时候可以用线性回归,特别是为什么可以用最小二乘法来计算损失函数\(J\)。
现在,让我们通过下面方程来假设输出变量和输入之间的关系:
\[y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)}\]
在这里\(\epsilon^{(i)}\)是误差项,代表在建模时没有考虑到的因素,或者是随机噪声。根据高斯分布(Gaussian distribution),现在假设\(\epsilon^{(i)}\)是独立同分布(IID,independently and indentically distributed),其中使高斯分布的均值\(\mu\)为0,方差为\(\sigma^2\),即\(\epsilon^{(i)}\in \mathcal{N}(0,\sigma^2)\),因此,\(\epsilon^{(i)}\)的密度是:
(\(\epsilon^{(i)}\)之所以假设为高斯分布是因为根据中心极限定理,大量相互独立的变量之和是符合正态分布的。)
\[p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}\right)\]
即给定\(x^{(i)}\)和参数\(\theta\)时,函数值应服从高斯分布:
\[p(y^{(i)}|x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right)\]
\(p(y^{(i)}|x^{(i)};\theta)\)是给定\(\theta\)和\(x^{(i)}\)的\(y^{(i)}\)的分布,其中\(\theta\)不属于条件,不是一个随机变量。
\(y^{(i)}\)的分布表示:\(y^{(i)}|x^{(i)};\theta \sim \mathcal{N}(\theta^Tx^{(i)},\sigma^2)\)
上面是一个样本的分布方程,现在给写一个\(X\)和\(\theta\),得到预测值\(\overrightarrow y\)的函数,其中\(\theta\)是定值,该方程也称为似然函数:
\[L(\theta)=L(\theta;X,\overrightarrow y)=p(\overrightarrow y|X;\theta)\]
注意,上式是基于\(\epsilon^{(i)}\)的独立性假设,方程也可以表示:
\[\begin{align}L(\theta) &=\coprod_{i=1}^m p(y^{(i)}|x^{(i)};\theta)\&=\coprod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp\big(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\big)\\end{align}\]
现在,为了找出参数\(\theta\)的最优解,通过极大似然来选择出使\(L(\theta)\)最大化的\(\theta\)值。首先,用对数似然函数代替似然函数
\[\begin{align}\ell(\theta) &=logL(\theta)\&=log\coprod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp\big(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\big)\&=\sum_{i=1}^m log\frac{1}{\sqrt{2\pi}\sigma}exp\big(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\big)\&=mlog\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}*\frac{1}{2}\sum_{i=1}^m (y^{(i)}-\theta^Tx^{(i)})^2 \end{align}\]
要极大化\(\ell(\theta)\),则需要极小化
\[\frac{1}{2}\sum_{i=1}^m (y^{(i)}-\theta^Tx^{(i)})^2\]
这就是最小二乘损失函数\(J(\theta)\)。
4 局部加权线性回归
对于一个从\(x\in \mathbb{R}\)预测\(y\)的问题,下面左图中,使用了\(y=\theta_0+\theta_1x\)来匹配数据集。然而实际上,图中的数据并不是一条直线。
现在如果添加多一个特征\(x^2\),即\(y=\theta_0+\theta_1x+\theta_2x^2\),结果能够更好的匹配数据,然而,如果添加过多的特征,如右图所示,虽然通过了数据集的每一个点,然而这并不是十分好的结果。
对于左图所示的情况,函数明显没有很好地描述数据,这样的情况称为欠拟合;而右图的情况被称为过拟合
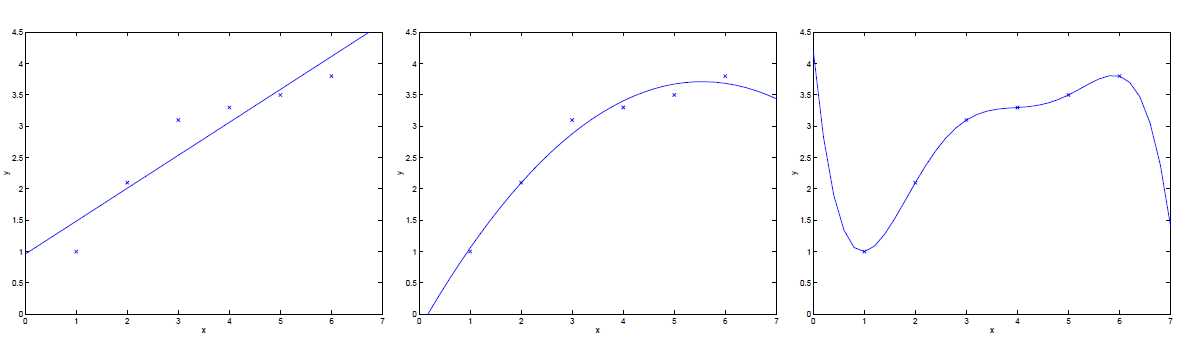
因此,特征的选择对于确保学习算法的良好性能很有帮助。
局部加权线性回归(LWR)能够使特性的选择对于算法来说不那么重要。
一般的线性回归算法,为了获取预测值,需要:
1,找到使\(\sum_{i=1} (y^{(i)}-\theta^Tx^{(i)})^2\)最小化的\(\theta\)
2, 输出\(\theta^Tx\)
局部加权线性回归算法:
1,找到使\(\sum_{i=1} w^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2\)最小化的\(\theta\)
2, 输出\(\theta^Tx\)
其中\(w^{(i)}\)是一个非负的权重值。
\[w^{(i)}=exp\big(-\frac{(x^{(i)}-x)^2}{2\tau^2}\big)\]
\(\tau\)参数控制了权值变化的速率,
当\(|x^{(i)}-x|\)很小时,\(w^{(i)}\)接近1,如果\(|x^{(i)}-x|\)很大,\(w^{(i)}\)接近0。其中\(x\)是我们需要评估的点。因此,选择\(\theta\)时对于离\(x\)近的训练样本有高的权重,而对于与训练样本距离大的有小的权重。这样就达到了局部加权的目的。
局部加权线性回归属于非参数学习算法,而之前的线性回归算法属于参数学习算法。
线性回归算法有固定的参数\(\theta\),一旦确定了\(\theta\)值后,我们不再需要保留训练数据,以对新的特征值进行预测。
而局部加权线性回归算法需要保留整个训练集以便计算\(w^{(i)}\)。
