看了这本书的第一个算法—k-近邻算法,这个算法总体构造思想是比较简单的,在ACM当中的话就对应了kd树这种结构。首先需要给定训练集,然后给出测试数据,求出训练集中与测试数据最相近的k个数据,根据这k个数据的属性来确定我们测试数据的属性。
书上的例子是给了四个点以及这四个点的标签,分别是A,A,B,B,现在给定一测试点,需要根据这四个训练集来判断该测试点的标签应该是A还是B。
1 from numpy import * 2 import operator 3 4 def createDataSet(): 5 group = array([[1.0,1.1], [1.0,1.0], [0,0], [0,0.1]]) 6 labels = [‘A‘, ‘A‘, ‘B‘, ‘B‘] 7 return group, labels 8 9 def classify0(inX, dataSet, labels, k): 10 dataSetSize = dataSet.shape[0] 11 diffMat = tile(inX, (dataSetSize,1)) - dataSet #统一矩阵,实现加减 12 sqDiffMat = diffMat**2 13 sqDistances = sqDiffMat.sum(axis=1) #进行累加,axis=0是按列,axis=1是按行 14 distances = sqDistances**0.5 #开根号 15 sortedDistIndicies = distances.argsort() #按升序进行排序,返回原下标 16 classCount = {} 17 for i in range(k): 18 voteIlabel = labels[sortedDistIndicies[i]] 19 classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 #get是字典中的方法,前面是要获得的值,后面是若该值不存在时的默认值 20 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
#在python3中没有iteritems,key在这里是按照字典的第二个元素来排序,降序排序 21 return sortedClassCount[0][0] #获得字典中第一对映射中的第一个值 22 23 24 if __name__ == "__main__": 25 dataSet, labels = createDataSet() 26 inX = [0.2, 0.2] 27 print(classify0(inX, dataSet, labels, 2))
代码详解:
①array
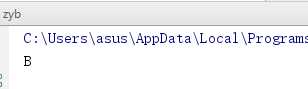
这是numpy库中,它就是用来构造矩阵的:
1 from numpy import array 2 3 a = array([[1,1], 4 [2,3]]) 5 b = array([[0,1], 6 [3,2]]) 7 c = a-b 8 print(c)
②tile()函数
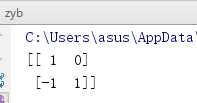
tile(A,repes)返回shape = repes的矩阵,每个元素是A
1 from numpy import tile 2 3 a = [1,2,3] 4 b = tile(a,(2,3)) 5 print(b)

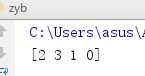
③argsort()
按序排列,返回原始下标
1 from numpy import argsort 2 3 a = [4,3,1,2] 4 b = argsort(a) 5 print(b)