An Old but Classic Problem
给定一个$n$个点,$m$条边的带正权有向图。给定$s$和$t$,询问$s$到$t$的所有权和为正路径中,第$k$短的长度。
Notice
定义两条路径不同,当且仅当它们的边集中存在一条边,使得它只在其中的一条路径上。
Solution#1 Shortest Path & A*
对于Dijstra算法,有一个结论就是,当一个点第$k$次出队的时候,此时路径长度就是$s$到它的第$k$短路。
那为什么还要A*呢?我试了试,写了个Dijstra,然后交了一发poj 2449,于是MLE了。。。如果您觉得我的Dijstra太丑了,您可以手写一个交一发。
所以用A*来优化优化状态数(其实就是玄学优化,需要你的人品还有出题人的素质)。
首先建反图,跑一次最短路算法,得到每个点到$t$的最短路的距离。
然后用当前走的距离加上到终点的最短路的长度作为优先级进行A*。
那如何得到答案?
- 当一个点第k次出队时,答案是它的优先级
- 当终点第k次出队时,答案是它已经走的路程
据说A*可以被卡成$O\left(nk\log n \right )$,只是我不会QAQ。
Code

1 /** 2 * poj 3 * Problem#2449 4 * Accepted 5 * Time: 250ms 6 * Memory: 9252k 7 */ 8 #include <iostream> 9 #include <fstream> 10 #include <sstream> 11 #include <algorithm> 12 #include <cstdio> 13 #include <cstdlib> 14 #include <cstring> 15 #include <ctime> 16 #include <cctype> 17 #include <cmath> 18 #include <vector> 19 #include <queue> 20 #include <stack> 21 #include <map> 22 #include <set> 23 #include <bitset> 24 using namespace std; 25 typedef bool boolean; 26 27 typedef class Edge { 28 public: 29 int end; 30 int next; 31 int w; 32 33 Edge(int end = 0, int next = -1, int w = 0):end(end), next(next), w(w) { } 34 }Edge; 35 36 const int N = 1e3, M = 1e5; 37 38 typedef class MapManager { 39 public: 40 int cnt; 41 int h[N + 5]; 42 Edge edge[M + 5]; 43 44 MapManager() { } 45 MapManager(int n):cnt(-1) { 46 // h = new int[(n + 1)]; 47 // edge = new Edge[(m + 1)]; 48 memset(h, -1, sizeof(int) * (n + 1)); 49 } 50 51 inline void addEdge(int u, int v, int w) { 52 edge[++cnt] = (Edge(v, h[u], w)); 53 // h[u] = (signed)edge.size() - 1; 54 h[u] = cnt; 55 } 56 57 inline int start(int node) { return h[node]; } 58 59 Edge& operator [] (int pos) { 60 return edge[pos]; 61 } 62 }MapManager; 63 #define m_endpos -1 64 65 int n, m; 66 MapManager g; 67 MapManager rg; 68 int s, t, k; 69 int ds[N + 5]; 70 71 inline void init() { 72 scanf("%d%d", &n, &m); 73 memset(g.h, -1, sizeof(int) * (n + 1)); 74 memset(rg.h, -1, sizeof(int) * (n + 1)); 75 for(int i = 1, u, v, w; i <= m; i++) { 76 scanf("%d%d%d", &u, &v, &w); 77 g.addEdge(u, v, w); 78 rg.addEdge(v, u, w); 79 } 80 scanf("%d%d%d", &s, &t, &k); 81 // ds = new int[(n + 1)]; 82 } 83 84 #define g rg 85 #define f ds 86 #define que que1 87 boolean vis[N + 5]; 88 queue<int> que; 89 boolean spfa(int s, int t) { 90 memset(f, 0x7f, sizeof(int) * (n + 1)); 91 memset(vis, false, sizeof(boolean) * (n + 1)); 92 que.push(s); 93 f[s] = 0; 94 while(!que.empty()) { 95 int e = que.front(); 96 que.pop(); 97 vis[e] = false; 98 for(int i = g.start(e); i != m_endpos; i = g[i].next) { 99 int& eu = g[i].end; 100 // cout << e << " " << eu << " " << i <<endl; 101 if(f[e] + g[i].w < f[eu]) { 102 f[eu] = f[e] + g[i].w; 103 if(!vis[eu]) { 104 que.push(eu); 105 vis[eu] = true; 106 } 107 } 108 } 109 } 110 return (f[t] != 0x7f7f7f7f); 111 } 112 #undef g 113 #undef f 114 #undef que 115 116 typedef class Status { 117 public: 118 int node; 119 int dis; 120 int priority; 121 122 Status(int node = 0, int dis = 0):node(node), dis(dis), priority(h()) { } 123 124 int h() { 125 return dis + ds[node]; 126 } 127 128 boolean operator < (Status b) const { 129 return priority > b.priority; 130 } 131 }Status; 132 133 int label[N + 5]; 134 priority_queue<Status> que; 135 int bfs(int s, int t) { 136 if(s == t) k++; 137 // label = new int[(n + 1)]; 138 memset(label, 0, sizeof(int) * (n + 1)); 139 que.push(Status(s, 0)); 140 while(!que.empty()) { 141 Status e = que.top(); 142 que.pop(); 143 label[e.node]++; 144 if(e.node == t && label[e.node] == k) 145 return e.dis; 146 for(int i = g.start(e.node); i != m_endpos; i = g[i].next) { 147 if(label[g[i].end] < k) 148 que.push(Status(g[i].end, e.dis + g[i].w)); 149 } 150 } 151 return -1; 152 } 153 154 inline void solve() { 155 if(!spfa(t, s)) { 156 puts("-1"); 157 return; 158 } 159 printf("%d", bfs(s, t)); 160 } 161 162 int main() { 163 init(); 164 solve(); 165 return 0; 166 }
Solution#2 Shortest Path & Protractable Heap
考虑建立反图,然后跑最短路算法得到以$t$为根的最短路径生成树。
当走了一条非树边$(u, v, w)$意味着什么?
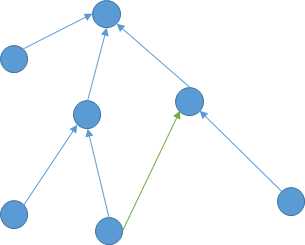
最终的路径长度就会因此增加$f[v] - f[u] + w$。
对于一条路径,我们依次将它经过的非树边记下来,约定得到的序列是这条路径的非树边序列。
考虑对于一个合法的非树边序列,我们可以找到唯一的一条$s$到$t$的路径与之对应。
因此,$k$短路的长度就等于第$k$小的代价和加上$s$到$t$的最短路的长度。
考虑如何来得到一个合法的非树边序列。
- 找到一条起点在当前点$p$到根$t$的路径上的非树边
- 令p等于这条边的终点。
我们可以通过这样的方法来得到所有的非树边序列。但是我们并不需要所有的非树边序列,因此当找到第$x$短路后再进行拓展状态,然后用优先队列来维护。
但是这样每次拓展时间复杂度可达$O(m)$,总时间复杂度可以达到$O\left(mk\log \left (mk \right ) \right )$。
令人无法接受。但是其中真正会被用到的状态十分少。
因此可以像UVa 11997那样进行优化。
当一个非树边序列出队时,代价和比它大的才可能有用。
因此,考虑一个非树边序列出队时通过下面的方法来进行得到新的序列:
- 追加操作:假如最后一条非树边的终点为$v$,找到一条起点在$v$到$t$的路径上代价最小的非树边追加在当前非树边序列后
- 替换操作:将最后一条非树边更换为代价比它大的1条非树边。
例如图中橙色虚线是被替换掉的非树边,紫色是新加入的非树边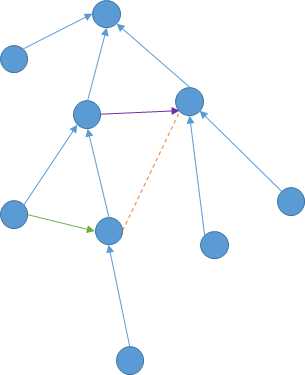
考虑用一些可持久化数据结构(如可持久化斜堆,可持久化线段树,可持久化Treap)来维护起点在点$u$到根的路径上的非树边的代价。
对于替换操作,
- 如果用的可持久化堆,那么把最后一条非树边替换为它所在的堆(你从哪个堆把它拿出来的)中它的左右子节点代表的边。
- 如果用的可持久化平衡树,那么把最后一条非树边直接替换为它的后继
- ......
这是一个很稳定的算法,时间复杂度$O\left ( n + m\log m + k\log k \right )$。就是常数有点大,sad.....
注意一些细节
- 计算代价时需要考虑终点是否可以到达$t$
- 考虑$s = t$时,要求的$k$短路包不包含0
- $k$短路不存在,队首为空
Code

1 /** 2 * poj 3 * Problem#2449 4 * Accepted 5 * Time: 438ms 6 * Memory: 15196k 7 */ 8 #include <algorithm> 9 #include <iostream> 10 #include <cstring> 11 #include <cstdio> 12 #include <vector> 13 #include <queue> 14 using namespace std; 15 typedef bool boolean; 16 17 #define pii pair<int, int> 18 #define fi first 19 #define sc second 20 21 typedef class Node { 22 public: 23 int val, ed; 24 Node *l, *r; 25 26 Node() { } 27 Node(int val, int ed, Node *l, Node *r):val(val), ed(ed), l(l), r(r) { } 28 }Node; 29 30 #define Limit 1000000 31 32 Node pool[Limit]; 33 Node* top = pool; 34 35 Node* newnode(int val, int ed) { 36 if(top >= pool + Limit) 37 return new Node(val, ed, NULL, NULL); 38 top->val = val, top->ed = ed, top->l = top->r = NULL; 39 return top++; 40 } 41 42 Node* merge(Node* a, Node* b) { 43 if (!a) return b; 44 if (!b) return a; 45 if (a->val > b->val) swap(a, b); 46 Node* p = newnode(a->val, a->ed); 47 p->l = a->l, p->r = a->r; 48 p->r = merge(p->r, b); 49 swap(p->l, p->r); 50 return p; 51 } 52 53 typedef class Status { 54 public: 55 int dist; 56 Node* p; 57 58 Status(int dist = 0, Node* p = NULL):dist(dist), p(p) { } 59 60 boolean operator < (Status b) const { 61 return dist > b.dist; 62 } 63 }Status; 64 65 typedef class Edge { 66 public: 67 int end, next, w; 68 69 Edge(int end = 0, int next = 0, int w = 0):end(end), next(next), w(w) { } 70 }Edge; 71 72 typedef class MapManager { 73 public: 74 int ce; 75 int* h; 76 Edge* es; 77 78 MapManager() { } 79 MapManager(int n, int m):ce(0) { 80 h = new int[(n + 1)]; 81 es = new Edge[(m + 5)]; 82 memset(h, 0, sizeof(int) * (n + 1)); 83 } 84 85 void addEdge(int u, int v, int w) { 86 es[++ce] = Edge(v, h[u], w); 87 h[u] = ce; 88 } 89 90 Edge& operator [] (int pos) { 91 return es[pos]; 92 } 93 }MapManager; 94 95 int n, m; 96 int s, t, k; 97 MapManager g; 98 MapManager rg; 99 boolean *vis; 100 int* f, *lase; 101 102 inline void init() { 103 scanf("%d%d", &n, &m); 104 g = MapManager(n, m); 105 rg = MapManager(n, m); 106 for (int i = 1, u, v, w; i <= m; i++) { 107 scanf("%d%d%d", &u, &v, &w); 108 g.addEdge(u, v, w); 109 rg.addEdge(v, u, w); 110 } 111 scanf("%d%d%d", &s, &t, &k); 112 } 113 114 queue<int> que; 115 void spfa(MapManager& g, int s) { 116 vis = new boolean[(n + 1)]; 117 f = new int[(n + 1)]; 118 lase = new int[(n + 1)]; 119 memset(f, 0x7f, sizeof(int) * (n + 1)); 120 memset(vis, false, sizeof(boolean) * (n + 1)); 121 que.push(s); 122 f[s] = 0, lase[s] = 0; 123 while (!que.empty()) { 124 int e = que.front(); 125 que.pop(); 126 vis[e] = false; 127 for (int i = g.h[e]; i; i = g[i].next) { 128 int eu = g[i].end, w = g[i].w; 129 if (f[e] + w < f[eu]) { 130 f[eu] = f[e] + w, lase[eu] = i; 131 if (!vis[eu]) { 132 vis[eu] = true; 133 que.push(eu); 134 } 135 } 136 } 137 } 138 } 139 140 Node** hs; 141 inline void rebuild() { 142 for (int i = 1; i <= n; i++) 143 for (int j = g.h[i]; j; j = g[j].next) { 144 int e = g[j].end; 145 if (lase[i] != j) 146 g[j].w += f[e] - f[i]; 147 } 148 149 hs = new Node*[(n + 1)]; 150 que.push(t); 151 hs[t] = NULL; 152 while (!que.empty()) { 153 int e = que.front(); 154 que.pop(); 155 if (lase[e]) 156 hs[e] = hs[g[lase[e]].end]; 157 for (int i = g.h[e]; i; i = g[i].next) 158 if (lase[e] != i && f[g[i].end] != 0x7f7f7f7f) 159 hs[e] = merge(hs[e], new Node(g[i].w, g[i].end, NULL, NULL)); 160 for (int i = rg.h[e]; i; i = rg[i].next) { 161 int eu = rg[i].end; 162 if (lase[eu] == i) 163 que.push(eu); 164 } 165 } 166 } 167 168 inline int kthpath(int k) { 169 if (s == t) 170 k++; 171 if (f[s] == 0x7f7f7f7f) 172 return -1; 173 if (k == 1) 174 return f[s]; 175 176 priority_queue<Status> q; 177 if (!hs[s]) 178 return -1; 179 180 q.push(Status(hs[s]->val, hs[s])); 181 while (--k && !q.empty()) { 182 Status e = q.top(); 183 q.pop(); 184 185 if(k == 1) 186 return e.dist + f[s]; 187 188 int eu = e.p->ed; 189 if (hs[eu]) 190 q.push(Status(e.dist + hs[eu]->val, hs[eu])); 191 if (e.p->l) 192 q.push(Status(e.dist - e.p->val + e.p->l->val, e.p->l)); 193 if (e.p->r) 194 q.push(Status(e.dist - e.p->val + e.p->r->val, e.p->r)); 195 } 196 return -1; 197 } 198 199 inline void solve() { 200 printf("%d\n", kthpath(k)); 201 } 202 203 int main() { 204 init(); 205 spfa(rg, t); 206 rebuild(); 207 solve(); 208 return 0; 209 }
特别鸣谢
YJQ
ZJC

