数据结构与算法（5）----->二叉树

1.  概念

　　二叉树节点的结构：

class Node{
    int value;　　　　　　    // value表示二叉树的节点值
    Node left;
    Node right;　　　　　    // left和right表示二叉树的两个孩子
    Node(int data){
       this.value = data;
    }
}

 　　　　　　如图：

 2.  二叉数的遍历

2.1  按顺序遍历二叉树

• 先序遍历：中、左、右
• 中序遍历：左、中、右
• 后序遍历：左、右、中
  • 以下图二叉树为例：
  • 

     

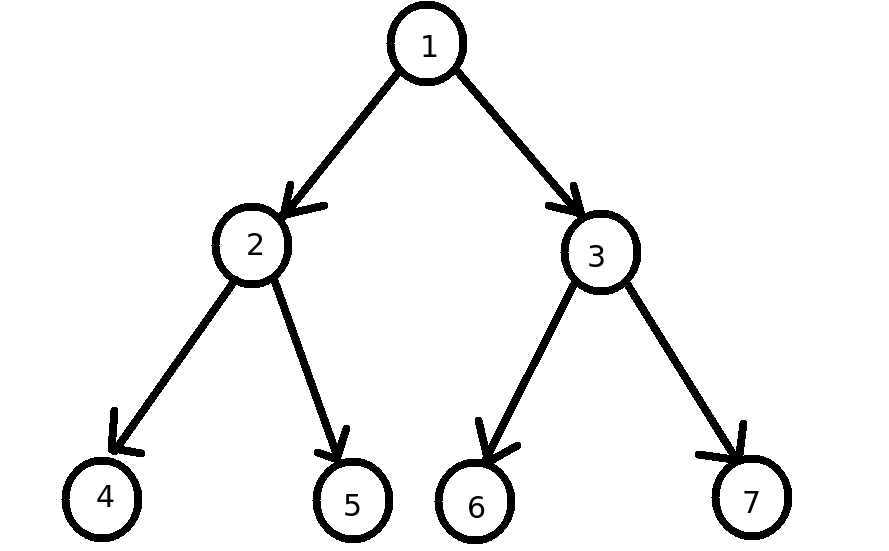
  • 先序遍历结果为： 1 ，2，4，5，3，6，7
  • 中序遍历结果为： 4，2，5，1，6，3，7
  • 后序遍历结果为： 4，5，2，6，7，3，1

2.2  按层遍历二叉树

1. 针对二叉树的宽度优先遍历;
2. 宽度优先遍历常使用队列结构;
3. （往往要求连同行号一起打印出来！！）

3.  平衡二叉树（AVL树）

　　概念：

1. 空树是平衡二叉树;
2. 如果一棵树不为空，并且其中所有的子树都满足各自的左子树与右子树的高度差都不超过1，是平衡二叉树;
   • 例如：
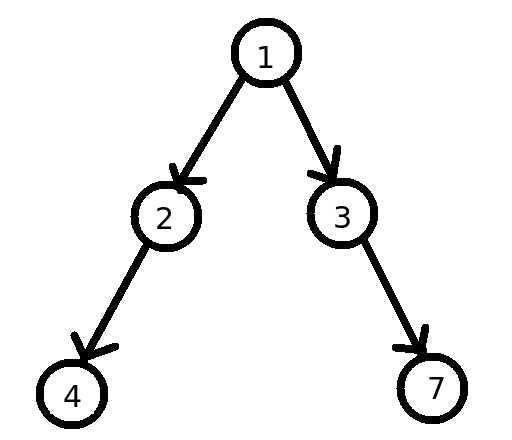   1. • • 　（平衡二叉树）

           

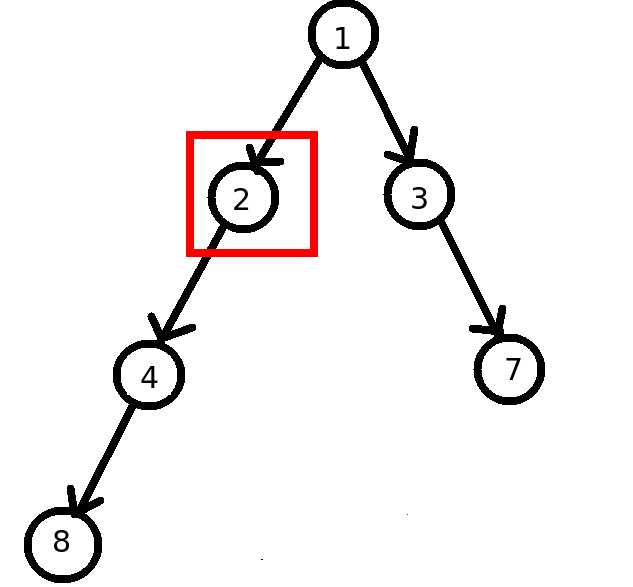        • （非平衡二叉树）
        • 因为，对于上图中，以2为节点的子树，其左子树为2，右子树为0，高度差大于1，我所以不是平衡二叉树;

4.  搜索二叉树

　　搜索二叉树的特征：

　　每棵子树的头节点的值都比各自左子树上的所有节点值要大，也要比各自右子树上的所有节点值要小．

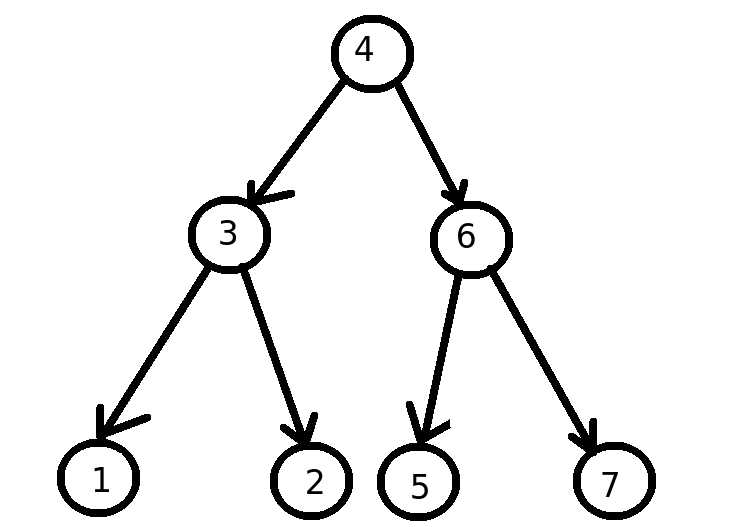
1. 搜索二叉树按照中序遍历得到的序列，一定是从小到大排列的．
2. 其中，红黑树/平衡二叉树（ＡＶＬ树）等，都是搜索二叉树的不同实现．

5.  满二叉树

　　概念：满二叉树是除了最后一层节点无任何子节点外，剩下每一层上的节点都有两个子节点．

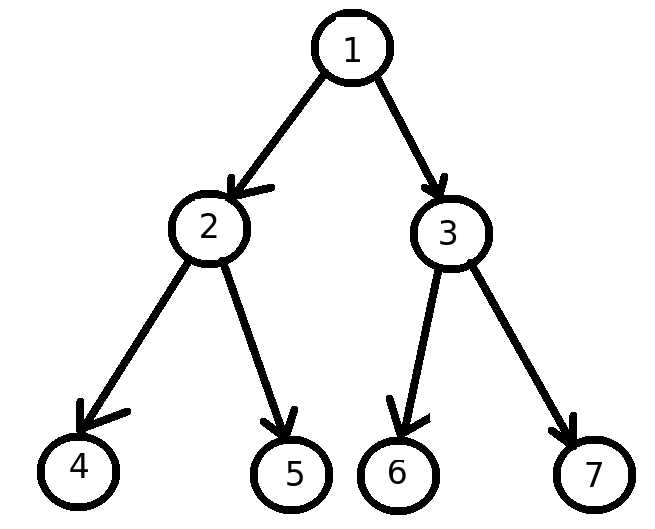
　　满二叉树的层数即为Ｌ，节点数即为Ｎ，则Ｎ＝2Ｌ－１；Ｌ＝log₂(N+1).

5.  完全二叉树

　　 概念：除了最后一层之外，其他每一层的节点数都是满的，最后一层如果也满了，是一颗满二叉树，也是完全二叉树．最后一层如果不满，缺少的节点也全部的集中右边，那也是一颗满二叉树．

　　如下，都是完全二叉树！！！