一、Bellman-Ford算法用到的“材料”:
1、一个结果数组dis,这个结果数组记录从源点到其他点的最短距离,如dis[10] 表示(加入开始节点标号为1)开始节点1到10号节点的最短距离。
2、C/C++中定义结构体Edge,表示边,内设变量from、to、cost,分别表示这条边的开始标号、终点标号、边长度
3、为了方便测验设置一个边的数组,C++定义:Edge edges[100];
二、Bellman-Ford算法图解
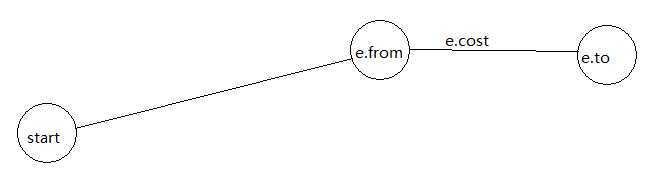
如图所示,针对一般情况分析,对一条边来说,我们想更新数组dis,让dis[i]变成从源点start到编号为index的点的最小值,所以就上图来说,当我们选择一条边e,如果start到e.from的距离可以估计(不是INF),那么start到to节点的距离就可以知道了,如果在之前dis[e.to]已经被更新过了,那么就要判断从start到e.from的距离加上e.cost的值 是否 小于 dis[e.to] 的值,如果小于就更新dis[e.to] = dis[e.from] + e.cost ,如果不是,那么就继续循环或跳出。
三、示例代码
#include<cstdio> #include<iostream> #include<cstring> #include<string> #define INF 0x7fffffff using namespace std; const int N = 100; typedef struct Edge{ int from; int to; int cost; }Edge; int dis[N]; Edge edges[N]; void init(int n,int st){ for(int i = 0 ;i <= n; ++i){ dis[i] = INF ; } dis[st] = 0 ; } void BellmanFord(int n, int m){ while(true){ bool update = false; //如果某一次循环没有更新dis数组,那么就代表这个图遍历完成了。时间复杂度O(V * E) for(int i = 0 ; i < m; ++i){ Edge e = edges[i]; if(dis[e.from] != INF && dis[e.from] + e.cost < dis[e.to]){ dis[e.to] = dis[e.from] + e.cost; update = true; } if(dis[e.to] != INF && dis[e.to] + e.cost < dis[e.from]){ dis[e.from] = dis[e.to] + e.cost; update = true; } } if(!update){ break; } } } void prt(int n){ for(int i = 1; i<= n; ++ i){ printf("%d ",dis[i]); } cout<<endl; } int main(){ int n , m; //n个顶点,m条边 while(cin>>n>>m){ init(n , 1); for(int i = 0 ; i< m ;++i){ cin>>edges[i].from>>edges[i].to>>edges[i].cost; } BellmanFord(n , m); prt(n); } return 0; } /* 测试 7 10 1 2 2 1 3 5 2 3 4 3 4 2 2 4 6 2 5 10 5 6 3 4 6 1 6 7 9 5 7 5 */
