一、动态规划算法
众所周知,递归算法时间复杂度很高为(2^n),而动态规划算法也能够解决此类问题,动态规划的算法的时间复杂度为(n^2)。动态规划算法是以空间置换时间的解决方式,一开始理解起来可能比较困,自己画画也许明白了很多。
二、动态规划算法分析
先举个例子:

{7,0,0,0,0},{3,8,0,0,0},{8,1,0,0,0},{2,7,4,4,0},{4,5,2,6,5} 这个二维数组,求一下,顶层到底层,只能通过两端来相加的最大值(也就是说这棵树的最长路径)。
分析:
(1)第一步:有底层向上层算起,因为这是一个金字塔的形状,底层向上算起,就可以最终到一个值,这个值就是最大值,
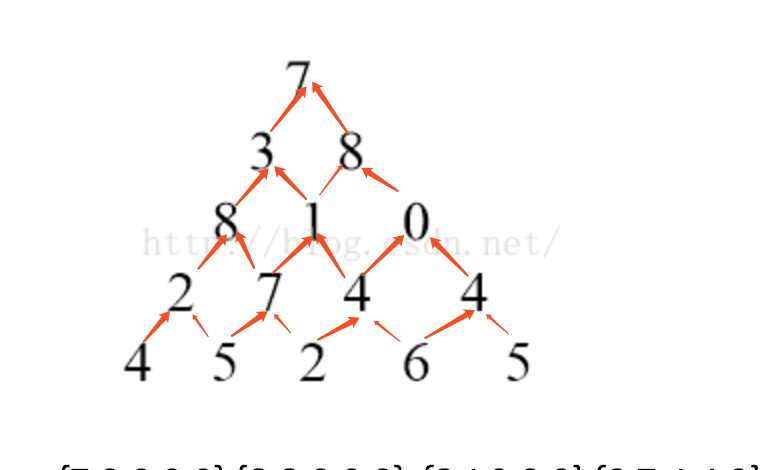
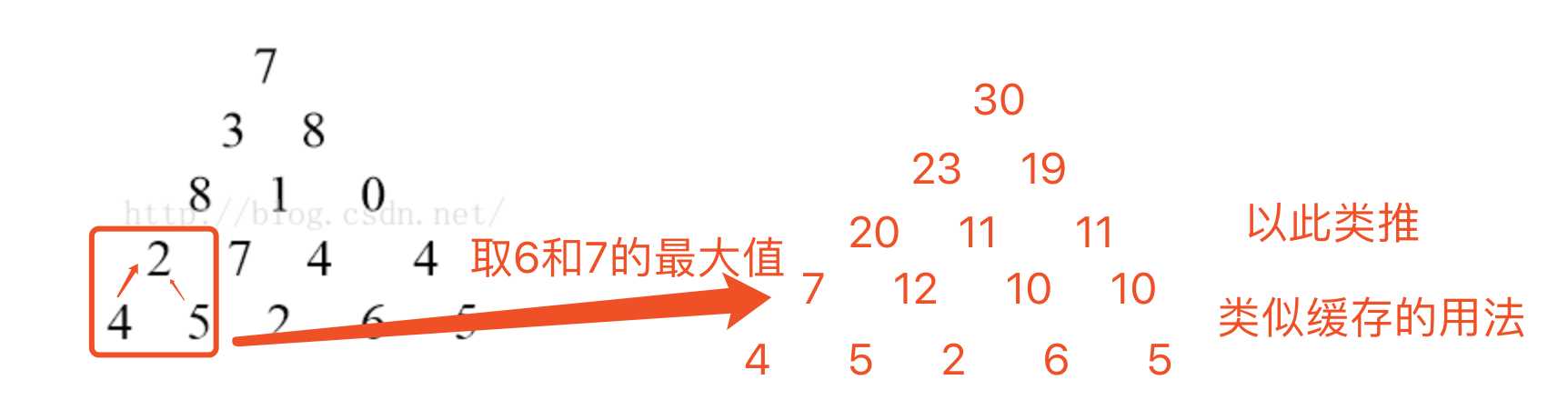
(2)每一层相加,然后比较取最大数。即:
三、代码实现
@Test public void test2(){ int[][] arr={ {7,0,0,0,0}, {3,8,0,0,0}, {8,1,0,0,0}, {2,7,4,4,0}, {4,5,2,6,5} }; int max = maxSumNew(arr,5); System.out.println(max); } /** * 动态规划 * @param arr * @param n * @param * @return */ public int maxSumNew(int arr[][],int n){ if(arr==null){ return 0; } int[][] max = new int[n][n]; for(int i = n-1; i >=0; i--){ for(int j = 0; j <= i; j++){ if(i==n-1){ max[n-1][j] = arr[n-1][j]; }else{ max[i][j] = Math.max(max[i+1][j],max[i+1][j+1]) + arr[i][j]; } } } return max[0][0]; }
以上是小弟的总结,如果有不正确的地方,还请大牛指正。
参考url:http://blog.csdn.net/baidu_28312631/article/details/47418773
