KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法,由他们的名字首字母组成)。
KMP算法的关键是利用已经部分匹配的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
在介绍KMP之前先说一说朴素解法,也就是最简单的暴力解法,朴素解法是采用穷举的方式一个一个对比达到查找的功能,子串与目标匹配失败后又要重新从子串的开头继续匹配,不考虑重复判断过的字符,所以效率非常的差劲。
下面是朴素解法的实现代码:
int sub_str_index(const char* s, const char* p) // s是源串,p是模式串、子串 { int ret = -1; // ret记录返回值,初始化为-1表示没有找到 int sl = strlen(s); int pl = strlen(p); int len = sl - pl; // len记录源串比子串长多少,用于判断子串最多可向后移动的位数,避免匹配过程中剩余源串长度不足 for(int i=0; (ret<0) && (i<=len); i++) // 如果没有找到匹配的,且源串还没有到越界下标 { bool equal = true; // equal用于记录临时的匹配情况,为了下面的循环,默认为真 for(int j=0; equal && (j<pl); j++) // 如果equal为真且子串没有越界就继续循环 equal = (s[i + j] == p[j]); // 如果当前源串的某个字符与子串对应的字符匹配,equal就为真 ret = (equal ? i : -1); // 如果子串全部匹配成功就返回匹配源串首字符的下标,否则返回-1表示失配 } return ret; }
接下来介绍KMP算法:
KMP算法是利用已知的信息减少无效匹配判断的一种算法。
这是阮一峰的讲解,我觉得非常好,供参考:http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
另外youtube上的黄浩杰也讲的不错,方便的朋友可以去看看。
下面这张图来自阮一峰博客,我做了一些修改,用它来举例子:

经过几次查找后,这里子串的D和源串的空格失配了,为了提高查找效率,我们发现直接把子串向后移动4位可以更高效的匹配,因为源串当前的3个字符都不能和子串匹配,从而省去了前面3次匹配的过程,实现效率的提升。
那我们如何知道要移动多少位呢,该如何计算呢。
这里就要用到KMP算法的部分匹配表了,部分匹配表用于记录『子串某个字符作为后缀的最后一个字符时』与『以子串第一个字符作为前缀』最多能匹配的字符个数;通过这个计数我们就能知道移动的位数了,因为它记录了当前字符最长匹配的字符个数,所以得出下面的公式:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
前缀是指除最后一个字符外所有的字符组合,而后缀则相反。例如上面的例子,对于子串而然:
由于我们匹配的时候是先匹配子串的第一个字符,成功匹配后向后移动匹配第二个,以此类推,所以我们的部分匹配表必须算出每个字符对应的部分匹配表。
下面来看一张图片
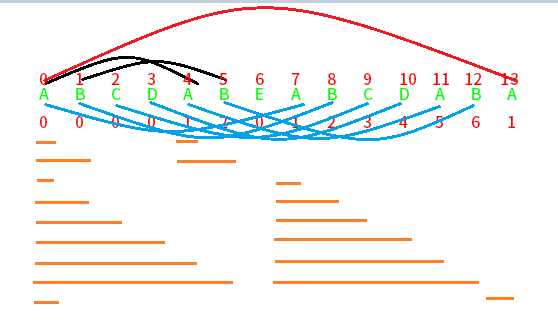
首先初始化匹配值为0,每次匹配的源串下标为上一个子串字符的部分匹配值,因为该值记录的永远是最长部分匹配值,所以只需要从已经匹配的源串后面继续即可,由于这个值是从1开始的,而下标是从0开始的,所以它指向的是已匹配源串字符的下一个。
下标0字符A没有可匹配的,所以直接设置为0。
下标1字符B没法和下标0字符匹配所以也是0。
下标2字符C不能和下标0字符匹配也不能以BC和AB匹配,所以也为0。
下标3字符D不能和下标0字符匹配,也不能CD与AB匹配,BCD和ABC也没法匹配,结果也是0。
下标4字符A可以和下标0字符匹配,所以匹配值加1,后续的组合再也不能匹配,所以第五个字符A的部分匹配值不再改变,结果为1。
下标5字符B因为之前的下标4字符匹配成功,所以要和下一个源串字符B进行匹配,这里匹配成功,匹配值在上一个字符匹配值的基础上加1变成2,而后续的组合不能再匹配,所以最终结果为2。
下标6字符E与前一个字符的部分匹配值2记录的字符(下标为部分匹配值-1)B不匹配,所以部分匹配值被重置为下标2-1处字符B的部分匹配值,也就是0;E与字符B的部分匹配值记录的字符A也不匹配,所以部分匹配值不变,仍为0。
以此类推下标7处的字符匹配成功,加1。。。。
最后下标13处的字符A与前一个字符B的部分匹配值记录的字符B(下标为6-1)不匹配,部分匹配值被重置为下标6-1处字符的部分匹配值2;下标13处字符A再与下标2处的字符C匹配又失败匹配值被重置为下标2处的部分匹配值0;下标13处字符A与下标0处的字符匹配成功,部分匹配值加1,最终结果为1。
网上很多人把这个部分匹配表写成next数组,我这里根据老师的代码写成了int类型的指针,用堆空间记录,长度与字符长度一致,每个单位为int类型,等效于int数组。
int* make_pmt(const char* p)· // 部分匹配表查找函数 { int len = strlen(p); int* ret = static_cast<int*>(malloc(sizeof(int) * len)); // 申请堆空间用于记录部分匹配表 if( ret != NULL ) // 只有堆空间申请成功才能操作 { int ll = 0; // ll==>longest length,最长部分匹配值 ret[0] = 0; // 第一个元素没有匹配的所以直接写为0 for(int i=1; i<len; i++) { while( (ll > 0) && (p[ll] != p[i]) ) // 部分匹配成功后又出现失败的 { ll = ret[ll-1]; // 把ll重置为上一个字符部分匹配值(也就是当前ll值)对应的字符(第ll个字符)的部分匹配值,注意下标从0开始所以要减1,注意小写ll和数字1的区别。 } if( p[ll] == p[i] ) { ll++; // 如果匹配成功,ll值加1; } ret[i] = ll; // 进入下一轮循环前要把ll值保存进部分匹配表 } } return ret; }
下面是kmp函数:
int String::kmp(const char* s, const char* p) { int ret = -1; int sl = strlen(s); int pl = strlen(p); int* pmt = make_pmt(p); // 获取子串的部分匹配表,注释该函数返回的是堆空间,用完需要释放 if( (pmt != NULL) && (0 < pl) && (pl <= sl) ) // 只有当部分匹配表获取成功、子串长度大于0且不超过源串长度的时候才需要计算 { for(int i=0, j=0; i<sl; i++) // for初始化i和j变量,i用于遍历每个源串,j用于记录已匹配的子串字符数 { while( (j > 0) && (s[i] != p[j]) ) // 有已匹配字符但是后续字符又匹配失败时 { j = pmt[j-1]; // 移动子串,使子串第一个字符对齐到源串下一个匹配的字符位置,这是一次性移动,不再是暴力搜索中的每次只移动一次 } if( s[i] == p[j] ) // 如果匹配成功,记录匹配子串字符个数的j加1 { j++; } if( j == pl ) // 如果匹配的子串字数与子串长度相等说明匹配成功 { ret = i + 1 - pl; // 返回匹配源串的第一个字符的下标并跳出循环结束寻找;此时i指向的是匹配的源串的最后一个字符,减去子串长度后等于第一个匹配的字符的前一个,所以要加1 break; } } } free(pmt); return ret; }
