投影方式- Unity3D游戏开发培训
作者:邓家海
2018-02-12 20:33:13
摘 要
透视投影是3D渲染的基本概念,也是3D程序设计的基础。掌握透视投影的原理对于深入理解其他3D渲染管线具有重要作用。本文详细介绍了透视投影的原理和算法实现,包括透视投影的标准模型、一般模型和屏幕坐标变换等,并通过VC实现了一个演示程序。
在Unity3D里面,投影方式决定了我们人眼看到的场景,投影方式一般分为透视投影和正交投影两种,透视投影相当于我们人的眼睛看到的东西。越远越小,越近越大。还会出现一个倒影。在物理学上面的小孔成像就是透视投影。正交投影是平行光源的投射,物体不会随着距离的改变而改变。在计算机三维图像里面,投影是可以看作是一种将三维坐标变成二维坐标的方法。
相机设置
透视投影:与人的视觉系统相似,多用在三维平面中对三维世界的呈现。模型是由视点E和视平面P两部分构成(要求E不在平面P上),视点就是观察者的位置,也就是三维世界的角度,视平面就是渲染三维对象的二维平面图,对于任意一点X,构造一条从E到X的射线R,R与平面P的交点X,p即是X点的透视投影结果。如图所示:
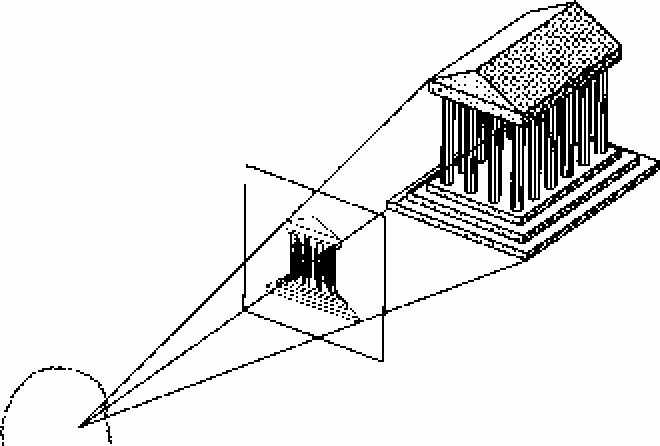
图 1-1
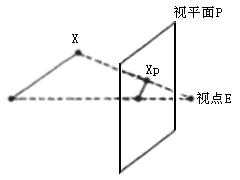
图 1-2
正交投影:用于二维世界的呈现。
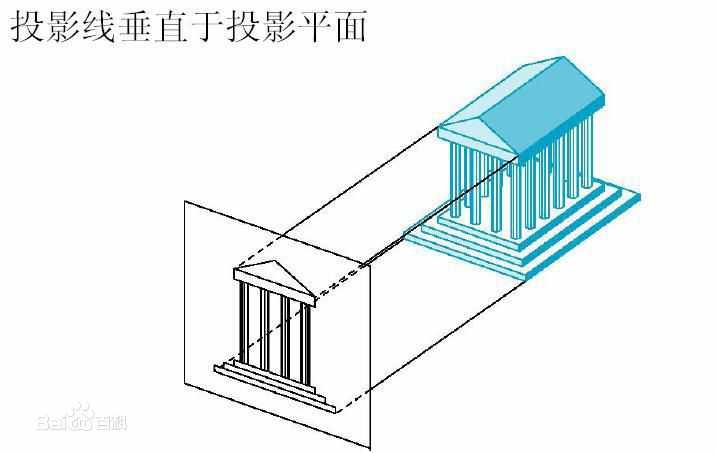
图 1-3
无论远近,大小是一样的
3D默认是透视投影(Perspective),2D默认是正交投影(Orthographic)。
透视投影的实现
6.1 载入3D模型
使用Matt Fairfax实现的Model_3DS类支持3DS模型文件的载入,该类的实现非常简单,而且很容易使用,具体可参考[7]。由于本文的DEMO只需要其中的模型载入功能,所以对源代码进行了删减,去掉了纹理加载(暂不需要)和渲染(我们自己实现)代码,在析构函数中添加了资源释放代码。
6.2 视图变换
为表示透视投影的一般模型,实现了KCamera类,除保存视点的位置和姿态,还保存视图变换矩阵m_kmView,随着视点位置和姿态的变化,视图矩阵也不断更新,更新算法详见第4节。对于世界坐标系中的任何一点v(x, y, z),通过v = m_kmView*v将其变换到透视投影的标准模型坐标系,详见KCamera::Transform函数。
6.3 透视变换
KFrustum类用来对透视投影的标准模型进行建模,其成员包括视平面的尺寸大小,以及近截面和远截面的z轴坐标。KFrustum通过Project函数将视图变换的结果变换为透视坐标。算法的原理见第3节,代码实现如下:
1 void KFrustum::Project(KVector3& v) 2 3 { 4 5 // xp = x*n/z, yp = y*n/z, zp = n. 6 7 float fFactor = GetNear()/v.z; 8 9 v.x *= fFactor; 10 11 v.y *= fFactor; 12 13 v.z = GetNear(); 14 15 }
6.4 屏幕变换
屏幕变换的算法通过宏实现,代码如下:
1 #define ToScreen(v, Ws, Hs) / 2 3 {/ 4 5 float x = (v.x/GetWidth()+0.5f)*(Ws-1);/ 6 7 float y = (v.y/GetHeight()+0.5f)*(Hs-1);/ 8 9 v.x = KMath::Round(x);/ 10 11 v.y = KMath::Round(y);/ 12 13 }
6.5 渲染
Demo中的渲染使用软件实现,没有使用任何第三方图形库,主代码在KCamera::Render函数中,它接收两次参数:Model_3DS和KSurface,对Model_3DS中的顶点进行透视投影,然后将结果绘制到Ksurface中。函数代码如下:
1 bool KCamera::Render(Model_3DS& m3DS, KSurface& kSurface) 2 3 { 4 5 kSurface.Fill(RGB(0,0,0)); // 背景为黑色 6 7 COLORREF crPen = RGB(255,0,0); // 用红色绘制模型 8 9 10 11 KMatrix4 m = m_kmView; 12 13 int Ws = kSurface.GetWidth(); 14 15 int Hs = kSurface.GetHeight(); 16 17 18 19 for(int i=0; i<m3DS.numObjects; i++) 20 21 { 22 23 Model_3DS::Object& obj = m3DS.Objects[i]; 24 25 26 27 for(int n=0; n<obj.numFaces; n+=3) 28 29 { 30 31 int index = obj.Faces[n]*3; 32 33 KVector4 v0(obj.Vertexes[index], obj.Vertexes[index+1], obj.Vertexes[index+2]); 34 35 index = obj.Faces[n+1]*3; 36 37 KVector4 v1(obj.Vertexes[index], obj.Vertexes[index+1], obj.Vertexes[index+2]); 38 39 index = obj.Faces[n+2]*3; 40 41 KVector4 v2(obj.Vertexes[index], obj.Vertexes[index+1], obj.Vertexes[index+2]); 42 43 44 45 Transform(v0, Ws, Hs); 46 47 Transform(v1, Ws, Hs); 48 49 Transform(v2, Ws, Hs); 50 51 52 53 // 绘制网线 54 55 kSurface.MoveTo(v0.x, v0.y); 56 57 kSurface.LineTo(v1.x, v1.y, crPen); 58 59 kSurface.LineTo(v2.x, v2.y, crPen); 60 61 kSurface.LineTo(v0.x, v0.y, crPen); 62 63 } 64 65 } 66 67 68 69 return true; 70 71 }
