1.队列:和栈中的情况不同,队列中的数据项不总是从数组下标0开始,移除一个数据项后,队头指针会指向下标较高的数据项,其特点:先入先出
2.图解
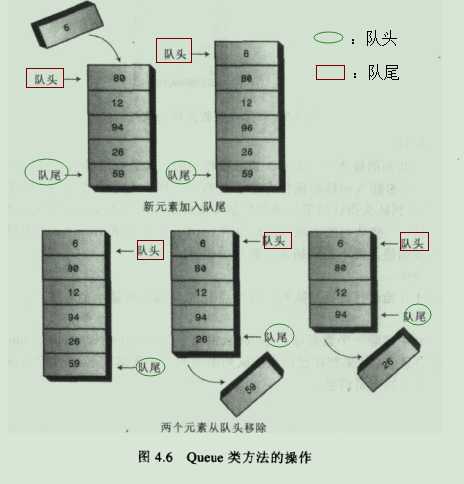
3.队列的实现代码:
3.1.Queue.java
1 package com.cn.queue; 2 /** 3 * 数据结构之队列实现 4 * @author Administrator 5 * 6 */ 7 public class Queue { 8 private int maxsize; 9 private long[] queuearray; 10 private int front; 11 private int rear; 12 private int nItems; 13 public Queue(int s){ 14 maxsize = s; 15 queuearray = new long[maxsize]; 16 front = 0; 17 rear = -1; 18 nItems = 0; 19 } 20 public void insert(long j){ 21 if (rear == maxsize - 1) 22 rear = -1; 23 queuearray[++ rear] = j; 24 nItems ++; 25 } 26 public long remove(){ 27 long temp = queuearray[front ++]; 28 if (front == maxsize) 29 front = 0; 30 nItems --; 31 return temp; 32 } 33 public long peekFront(){ 34 return queuearray[front]; 35 } 36 public boolean isEmpty(){ 37 return (nItems == 0); 38 } 39 public boolean isFull(){ 40 return (nItems == maxsize); 41 } 42 public int size(){ 43 return nItems; 44 } 45 46 }
3.2.QueueTest.java
1 package com.cn.queue; 2 3 public class QueueTest { 4 public static void main(String[] args) { 5 Queue q = new Queue(100); 6 q.insert(100); 7 q.insert(200); 8 q.insert(300); 9 while (q.size()!=0){ 10 System.out.print(q.remove()+" "); 11 } 12 System.out.println(""); 13 System.out.println(q.isEmpty()); 14 } 15 }
4.队列插入和删除的时间复杂度和栈的一样,都是O(1)
5.优先级队列:优先级队列是比栈和队列更加专用的数据结构,他有一个队头和队尾,并且也是从队头移除数据项,不过在优先级队列中,数据项按关键字的值有序,这样关键字最小的数据项总是在队头,而最大的就在队尾。做插入操作时会按照顺序插入到合适的位置以确保队列的顺序。除了可以快速访问最小关键值的数据项,优先队列还必须实现非常快的插入数据项,由此,优先级队列通常使用一种称为堆得数据结构实现。本程序暂时使用数组实现,该实现的插入比较慢,适用于数据量小,并且对速度要求并不高场景。
6.优先级队列的实现:
6.1.PriorityQ.java
1 package com.cn.queue; 2 /** 3 * 优先级队列的实现代码 4 * @author Administrator 5 * 6 */ 7 public class PriorityQ { 8 private int maxsize; 9 private long[] queuearray; 10 private int nItems; 11 public PriorityQ(int s){ 12 maxsize = s; 13 queuearray = new long[maxsize]; 14 nItems = 0; 15 } 16 public void insert(long item){ 17 int k; 18 if (nItems == 0) 19 queuearray[nItems ++] = item; 20 else{ 21 for(k = nItems - 1;k >= 0;k --){ 22 if (item > queuearray[k]) 23 queuearray[k + 1] = queuearray[k]; 24 else 25 break; 26 } 27 queuearray[k + 1] = item; 28 nItems ++; 29 } 30 } 31 public long remove(){ 32 return queuearray[-- nItems]; 33 } 34 public long peekmin(){ 35 return queuearray[nItems - 1]; 36 } 37 public boolean isEmpty(){ 38 return (nItems == 0); 39 } 40 public boolean isFull(){ 41 return (nItems == maxsize); 42 } 43 }
6.2图解
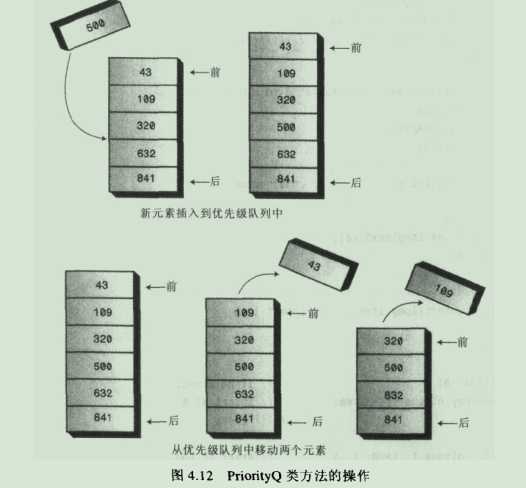
7.优先级队列的效率:插入操作时间复杂度位O(N),删除操作时间复杂度为O(1),后续堆数据结构将改进他。
