树上最近公共祖先（LCA）的算法

　　有错请大力指出【鞠躬】第一次写正经博客非常慌张

LCA（Least Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。

对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。

另一种理解方式是把T理解为一个无向无环图，而LCA(T,u,v)即u到v的最短路上深度最小的点。

——百度百科

LCA的四种算法：

• 记录dfs序转化为rmq问题（st表）
• tarjan算法
• 倍增算法
• 树链剖分

一、记录dfs序转化为rmq问题

　　1.dfs序是什么？

　　其实本人对dfs序的定义也不怎么清晰……望告知orz

　　首先我们需要一颗树……比如说它长这样：

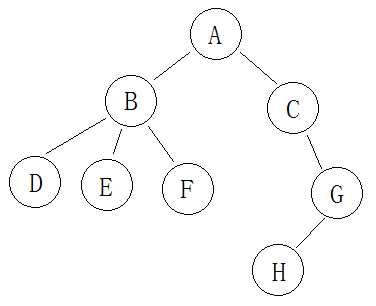
　　定义rt（root）为树根，则在这棵树中rt = 1。别说了我知道图上是A

　　本题需要用到的dfs序需在进入每个节点即搜完某一个儿子的时候记录这个节点。从rt开始进行dfs（深度优先搜索），则得到的dfs序列为A B D B E B F B A C G H G C A。

　　且让我们跟着跑一遍。

　　　　1.dfs(A) ， 序列为A

　　　　2.找到A的儿子B，dfs(B)，序列为A B

　　　　3.找到B的儿子D，dfs(D)，序列为A B D

　　　　4.发现D没有儿子，返回B，序列为A B D B

　　　　5.6.7.8. dfs(E)，返回B，dfs(F)，返回B，序列为A B D B E B F B

　　　　9.搜完B的儿子，返回A，序列为A B D B E B F B A

　　　　10.11.12. dfs(C)，dfs(G)，dfs(H)，序列为A B D B E B F B A C G H

　　　　13.14.15 返回G，返回C，返回A，序列为A B D B E B F B A C G H G C A

　　结束。

　　定义x为当前节点标号，dep为当前深度，h[i]为树高，in[i]为每个节点被访问到的序号，d[i]为dfs序。

　　代码如下：

void dfs(int x , int dep)
{
    d[++ cnt] = x ;
    h[x] = dep , in[x] = cnt ;
    for(int i = fst[x] ; i ; i = e[i].nx)
    {
        if(e[i].x == fa[x]) continue ;
        fa[e[i].x] = x ;
        dfs(e[i].x , dep + 1) ;
        d[++ cnt] = x ;
    }
}

View Code

 　　除了搜完根节点后结束dfs外，每个点被搜到和退出时均会在dfs序中加入一个数，因此该dfs序的长度为2 * n - 1。

　　设点u、点v的最近公共祖先为点x，并且u在v之前被dfs到。因为x为u、v的祖先，所以dfs时先找到x，再从x往下找到u，即dfs(u)时已经过了x。记录u后，返回到x再向下找到v。故在dfs序中，in[u]和in[v]之间必出现过x。而dfs(v)后返回时，x的子树还没有被搜完，所以不会出现x的祖先。这样即可保证在in[u]、in[v]中高度最小的点即为u、v的最近公共祖先。

　　这样我们有了一个正确的算法，但如果对于每个询问区间，都一位一位寻找最值，效率为O(mn)，显然不能接受。