卷积神经网络可谓是现在深度学习领域中大红大紫的网络框架,尤其在计算机视觉领域更是一枝独秀。CNN从90年代的LeNet开始,21世纪初沉寂了10年,直到12年AlexNet开始又再焕发第二春,从ZF Net到VGG,GoogLeNet再到ResNet和最近的DenseNet,网络越来越深,架构越来越复杂,解决反向传播时梯度消失的方法也越来越巧妙。新年有假期,就好好总结一波CNN的各种经典架构吧,领略一下CNN的发展历程中各路大神之间的智慧碰撞之美。
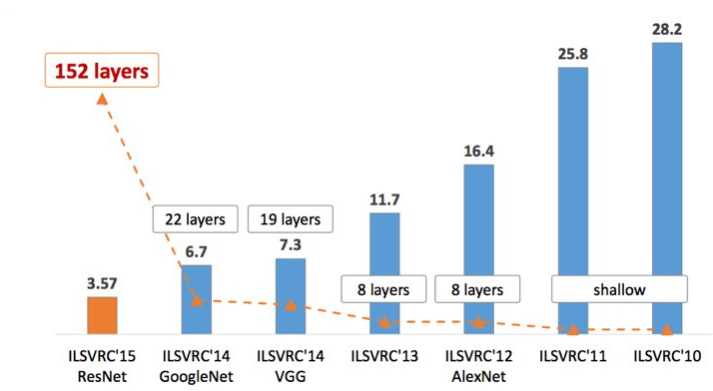
上面那图是ILSVRC历年的Top-5错误率,我们会按照以上经典网络出现的时间顺序对他们进行介绍。
本文将会谈到以下经典的卷积神经网络:
- LeNet
- AlexNet
- ZF
- VGG
- GoogLeNet
- ResNet
- DenseNet
开山之作:LeNet
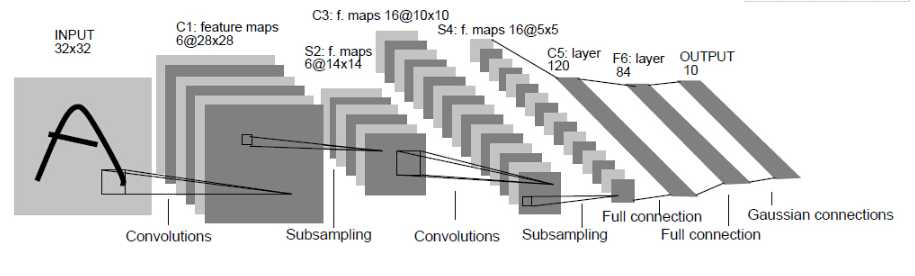
闪光点:定义了CNN的基本组件,是CNN的鼻祖。
LeNet是卷积神经网络的祖师爷LeCun在1998年提出,用于解决手写数字识别的视觉任务。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。如今各大深度学习框架中所使用的LeNet都是简化改进过的LeNet-5(-5表示具有5个层),和原始的LeNet有些许不同,比如把激活函数改为了现在很常用的ReLu。
LeNet-5跟现有的conv->pool->ReLU的套路不同,它使用的方式是conv1->pool->conv2->pool2再接全连接层,但是不变的是,卷积层后紧接池化层的模式依旧不变。

以上图为例,对经典的LeNet-5做深入分析:
- 首先输入图像是单通道的28*28大小的图像,用矩阵表示就是[1,28,28]
- 第一个卷积层conv1所用的卷积核尺寸为5*5,滑动步长为1,卷积核数目为20,那么经过该层后图像尺寸变为24,28-5+1=24,输出矩阵为[20,24,24]。
- 第一个池化层pool核尺寸为2*2,步长2,这是没有重叠的max pooling,池化操作后,图像尺寸减半,变为12×12,输出矩阵为[20,12,12]。
- 第二个卷积层conv2的卷积核尺寸为5*5,步长1,卷积核数目为50,卷积后图像尺寸变为8,这是因为12-5+1=8,输出矩阵为[50,8,8].
- 第二个池化层pool2核尺寸为2*2,步长2,这是没有重叠的max pooling,池化操作后,图像尺寸减半,变为4×4,输出矩阵为[50,4,4]。
- pool2后面接全连接层fc1,神经元数目为500,再接relu激活函数。
- 再接fc2,神经元个数为10,得到10维的特征向量,用于10个数字的分类训练,送入softmaxt分类,得到分类结果的概率output。
LeNet的Keras实现:
def LeNet():
model = Sequential()
model.add(Conv2D(32,(5,5),strides=(1,1),input_shape=(28,28,1),padding=‘valid‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,(5,5),strides=(1,1),padding=‘valid‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(100,activation=‘relu‘))
model.add(Dense(10,activation=‘softmax‘))
return model王者归来:AlexNet
AlexNet在2012年ImageNet竞赛中以超过第二名10.9个百分点的绝对优势一举夺冠,从此深度学习和卷积神经网络名声鹊起,深度学习的研究如雨后春笋般出现,AlexNet的出现可谓是卷积神经网络的王者归来。
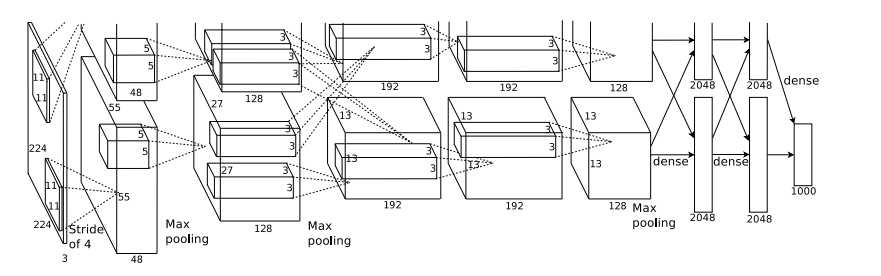
闪光点:
- 更深的网络
- 数据增广
- ReLU
- dropout
- LRN
以上图AlexNet架构为例,这个网络前面5层是卷积层,后面三层是全连接层,最终softmax输出是1000类,取其前两层进行详细说明。
AlexNet共包含5层卷积层和三层全连接层,层数比LeNet多了不少,但卷积神经网络总的流程并没有变化,只是在深度上加了不少。
AlexNet针对的是1000类的分类问题,输入图片规定是256×256的三通道彩色图片,为了增强模型的泛化能力,避免过拟合,作者使用了随机裁剪的思路对原来256×256的图像进行随机裁剪,得到尺寸为3×224×224的图像,输入到网络训练。
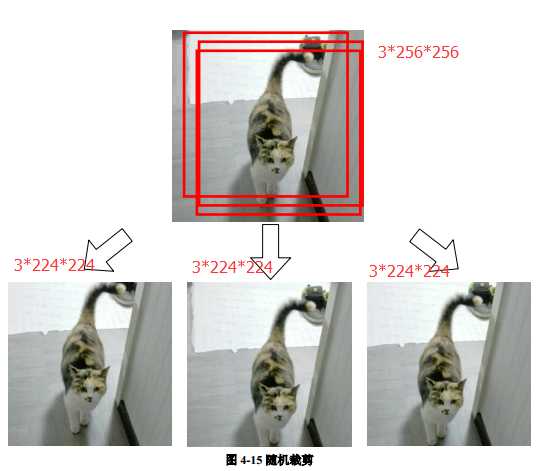
因为使用多GPU训练,所以可以看到第一层卷积层后有两个完全一样的分支,以加速训练。
- 针对一个分支分析:第一层卷积层conv1的卷积核尺寸为11×11,滑动步长为4,卷积核数目为48。卷积后得到的输出矩阵为[48,55,55]。这里的55是个难以理解的数字,作者也没有对此说明,如果按照正常计算的话(224-11)/4+1 != 55的,所以这里是做了padding再做卷积的,即先padiing图像至227×227,再做卷积(227-11)/4+1 = 55。这些像素层经过relu1单元的处理,生成激活像素层,尺寸仍为2组48×55×55的像素层数据
。然后经过归一化处理,归一化运算的尺度为5*5。第一卷积层运算结束后形成的像素层的规模为48×27×27。 输入矩阵是[48,55,55].接着是池化层,做max pooling操作,池化运算的尺度为3*3,运算的步长为2,则池化后图像的尺寸为(55-3)/2+1=27。所以得到的输出矩阵是[48,27,27]。后面层不再重复叙述。
AlexNet用到训练技巧:
- 数据增广技巧来增加模型泛化能力。
- 用ReLU代替Sigmoid来加快SGD的收敛速度
- Dropout:Dropout原理类似于浅层学习算法的中集成算法,该方法通过让全连接层的神经元(该模型在前两个全连接层引入Dropout)以一定的概率失去活性(比如0.5)失活的神经元不再参与前向和反向传播,相当于约有一半的神经元不再起作用。在测试的时候,让所有神经元的输出乘0.5。Dropout的引用,有效缓解了模型的过拟合。
- Local Responce Normalization:局部响应归一层的基本思路是,假如这是网络的一块,比如是 13×13×256, LRN 要做的就是选取一个位置,比如说这样一个位置,从这个位置穿过整个通道,能得到 256 个数字,并进行归一化。进行局部响应归一化的动机是,对于这张 13×13 的图像中的每个位置来说,我们可能并不需要太多的高激活神经元。但是后来,很多研究者发现 LRN 起不到太大作用,因为并不重要,而且我们现在并不用 LRN 来训练网络。
AlexNet的Keras实现:
def AlexNet():
model = Sequential()
model.add(Conv2D(96,(11,11),strides=(4,4),input_shape=(227,227,3),padding=‘valid‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Conv2D(256,(5,5),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Conv2D(384,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(384,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(256,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Flatten())
model.add(Dense(4096,activation=‘relu‘))
model.add(Dropout(0.5))
model.add(Dense(4096,activation=‘relu‘))
model.add(Dropout(0.5))
model.add(Dense(1000,activation=‘softmax‘))
return model
稳步前行:ZF-Net
ZFNet是2013ImageNet分类任务的冠军,其网络结构没什么改进,只是调了调参,性能较Alex提升了不少。ZF-Net只是将AlexNet第一层卷积核由11变成7,步长由4变为2,第3,4,5卷积层转变为384,384,256。这一年的ImageNet还是比较平静的一届,其冠军ZF-Net的名堂也没其他届的经典网络架构响亮。
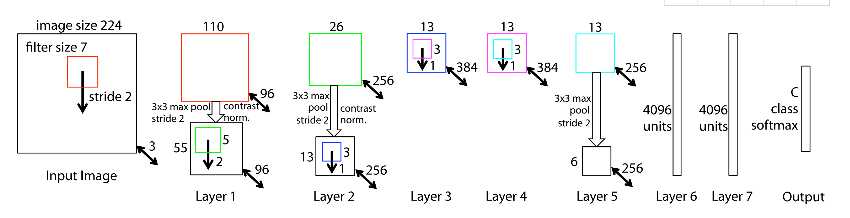
ZF-Net的Keras实现:
def ZF_Net():
model = Sequential()
model.add(Conv2D(96,(7,7),strides=(2,2),input_shape=(224,224,3),padding=‘valid‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Conv2D(256,(5,5),strides=(2,2),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Conv2D(384,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(384,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(256,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Flatten())
model.add(Dense(4096,activation=‘relu‘))
model.add(Dropout(0.5))
model.add(Dense(4096,activation=‘relu‘))
model.add(Dropout(0.5))
model.add(Dense(1000,activation=‘softmax‘))
return model
越走越深:VGG-Nets
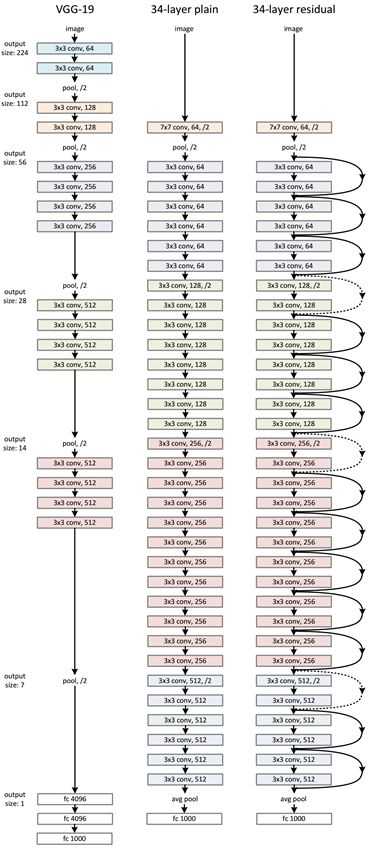
VGG-Nets是由牛津大学VGG(Visual Geometry Group)提出,是2014年ImageNet竞赛定位任务的第一名和分类任务的第二名的中的基础网络。VGG可以看成是加深版本的AlexNet. 都是conv layer + FC layer,在当时看来这是一个非常深的网络了,因为层数高达十多层,我们从其论文名字就知道了(《Very Deep Convolutional Networks for Large-Scale Visual Recognition》),当然以现在的目光看来VGG真的称不上是一个very deep的网络。
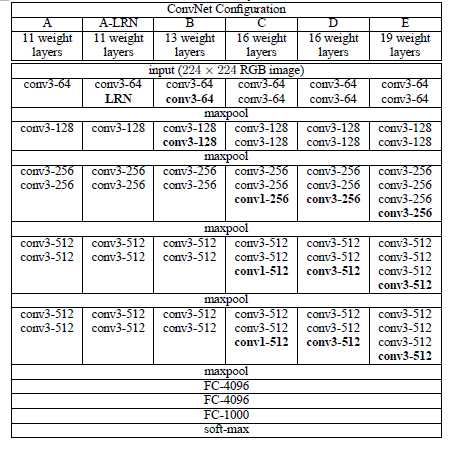
上面一个表格是描述的是VGG-Net的网络结构以及诞生过程。为了解决初始化(权重初始化)等问题,VGG采用的是一种Pre-training的方式,这种方式在经典的神经网络中经常见得到,就是先训练一部分小网络,然后再确保这部分网络稳定之后,再在这基础上逐渐加深。表1从左到右体现的就是这个过程,并且当网络处于D阶段的时候,效果是最优的,因此D阶段的网络也就是VGG-16了!E阶段得到的网络就是VGG-19了!VGG-16的16指的是conv+fc的总层数是16,是不包括max pool的层数!
下面这个图就是VGG-16的网络结构。
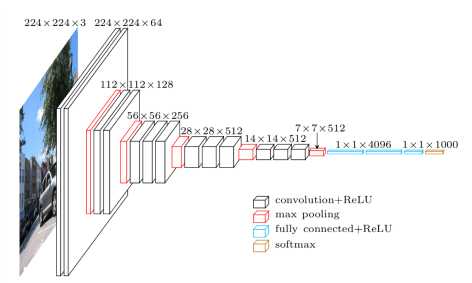
由上图看出,VGG-16的结构非常整洁,深度较AlexNet深得多,里面包含多个conv->conv->max_pool这类的结构,VGG的卷积层都是same的卷积,即卷积过后的输出图像的尺寸与输入是一致的,它的下采样完全是由max pooling来实现。
VGG网络后接3个全连接层,filter的个数(卷积后的输出通道数)从64开始,然后没接一个pooling后其成倍的增加,128、512,VGG的注意贡献是使用小尺寸的filter,及有规则的卷积-池化操作。
闪光点:
- 卷积层使用更小的filter尺寸和间隔
与AlexNet相比,可以看出VGG-Nets的卷积核尺寸还是很小的,比如AlexNet第一层的卷积层用到的卷积核尺寸就是11*11,这是一个很大卷积核了。而反观VGG-Nets,用到的卷积核的尺寸无非都是1×1和3×3的小卷积核,可以替代大的filter尺寸。
3×3卷积核的优点:
- 多个3×3的卷基层比一个大尺寸filter卷基层有更多的非线性,使得判决函数更加具有判决性
- 多个3×3的卷积层比一个大尺寸的filter有更少的参数,假设卷基层的输入和输出的特征图大小相同为C,那么三个3×3的卷积层参数个数3×(3×3×C×C)=27CC;一个7×7的卷积层参数为49CC;所以可以把三个3×3的filter看成是一个7×7filter的分解(中间层有非线性的分解)
1*1卷积核的优点:
- 作用是在不影响输入输出维数的情况下,对输入进行线性形变,然后通过Relu进行非线性处理,增加网络的非线性表达能力。
VGG-16的Keras实现:
def VGG_16():
model = Sequential()
model.add(Conv2D(64,(3,3),strides=(1,1),input_shape=(224,224,3),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(64,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(128,(3,2),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(128,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(256,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(256,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(256,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(512,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(512,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(512,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(512,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(512,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(Conv2D(512,(3,3),strides=(1,1),padding=‘same‘,activation=‘relu‘,kernel_initializer=‘uniform‘))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(4096,activation=‘relu‘))
model.add(Dropout(0.5))
model.add(Dense(4096,activation=‘relu‘))
model.add(Dropout(0.5))
model.add(Dense(1000,activation=‘softmax‘))
return model
大浪推手:GoogLeNet
GoogLeNet在2014的ImageNet分类任务上击败了VGG-Nets夺得冠军,其实力肯定是非常深厚的,GoogLeNet跟AlexNet,VGG-Nets这种单纯依靠加深网络结构进而改进网络性能的思路不一样,它另辟幽径,在加深网络的同时(22层),也在网络结构上做了创新,引入Inception结构代替了单纯的卷积+激活的传统操作(这思路最早由Network in Network提出)。GoogLeNet进一步把对卷积神经网络的研究推上新的高度。
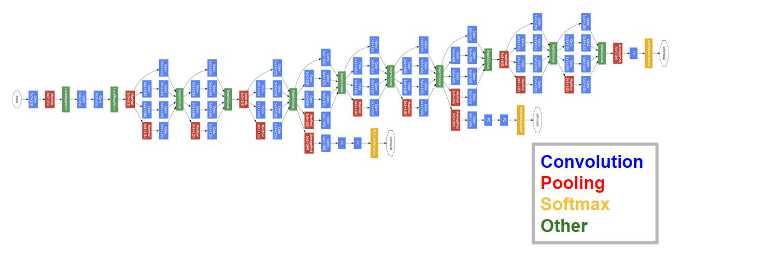
闪光点:
- 引入Inception结构
- 中间层的辅助LOSS单元
- 后面的全连接层全部替换为简单的全局平均pooling
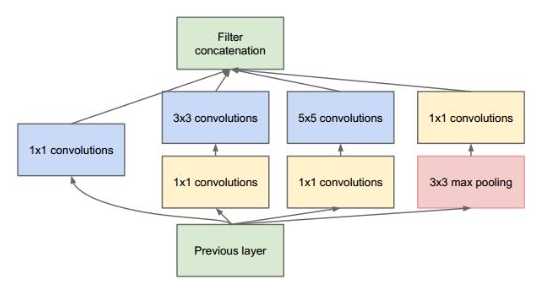
上图结构就是Inception,结构里的卷积stride都是1,另外为了保持特征响应图大小一致,都用了零填充。最后每个卷积层后面都立刻接了个ReLU层。在输出前有个叫concatenate的层,直译的意思是“并置”,即把4组不同类型但大小相同的特征响应图一张张并排叠起来,形成新的特征响应图。Inception结构里主要做了两件事:1. 通过3×3的池化、以及1×1、3×3和5×5这三种不同尺度的卷积核,一共4种方式对输入的特征响应图做了特征提取。2. 为了降低计算量。同时让信息通过更少的连接传递以达到更加稀疏的特性,采用1×1卷积核来实现降维。
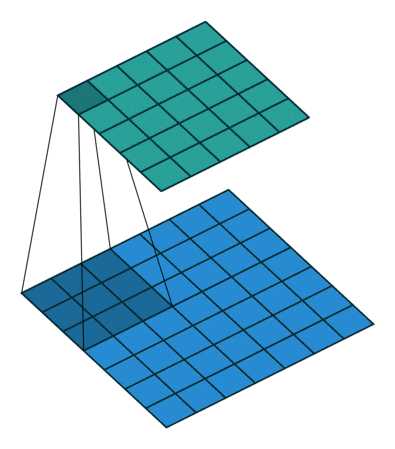
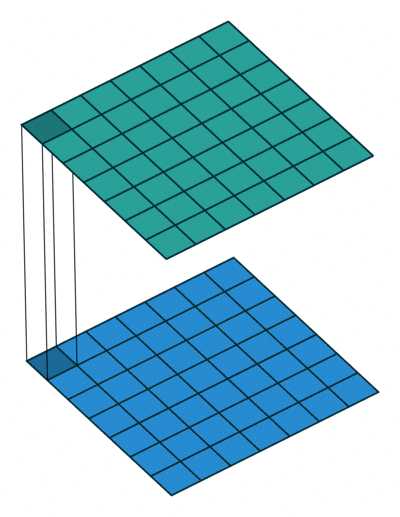
这里想再详细谈谈1×1卷积核的作用,它究竟是怎么实现降维的。下面图1是3×3卷积核的卷积,图2是1×1卷积核的卷积过程。对于单通道输入,1×1的卷积确实不能起到降维作用,但对于多通道输入,就不不同了。考虑[50,200,200]的矩阵输入,我们可以使用20个1×1的卷积核进行卷积,得到输出[20,200,200]。有人问,我用20个3×3的卷积核不是也能得到[20,200,200]的矩阵输出吗,为什么就1×1的可以降维?我们计算一下卷积参数就知道了,对于1×1的参数总数:20×200×200×(1×1),对于3×3的参数总数:20×200×200×(3×3),可以看出,使用1×1的参数总数仅为3×3的总数的九分之一!这就是降维!
GoogLeNet网络结构中有3个LOSS单元,这样的网络设计是为了帮助网络的收敛。在中间层加入辅助计算的LOSS单元,目的是计算损失时让低层的特征也有很好的区分能力,从而让网络更好地被训练。在论文中,这两个辅助LOSS单元的计算被乘以0.3,然后和最后的LOSS相加作为最终的损失函数来训练网络。
GoogLeNet还有一个闪光点值得一提,那就是将后面的全连接层全部替换为简单的全局平均pooling,在最后参数会变的更少。而在AlexNet中最后3层的全连接层参数差不多占总参数的90%,使用大网络在宽度和深度允许GoogleNet移除全连接层,但并不会影响到结果的精度,在ImageNet中实现93.3%的精度,而且要比VGG还要快。
GoogLeNet的Keras实现:
def Conv2d_BN(x, nb_filter,kernel_size, padding=‘same‘,strides=(1,1),name=None):
if name is not None:
bn_name = name + ‘_bn‘
conv_name = name + ‘_conv‘
else:
bn_name = None
conv_name = None
x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation=‘relu‘,name=conv_name)(x)
x = BatchNormalization(axis=3,name=bn_name)(x)
return x
def Inception(x,nb_filter):
branch1x1 = Conv2d_BN(x,nb_filter,(1,1), padding=‘same‘,strides=(1,1),name=None)
branch3x3 = Conv2d_BN(x,nb_filter,(1,1), padding=‘same‘,strides=(1,1),name=None)
branch3x3 = Conv2d_BN(branch3x3,nb_filter,(3,3), padding=‘same‘,strides=(1,1),name=None)
branch5x5 = Conv2d_BN(x,nb_filter,(1,1), padding=‘same‘,strides=(1,1),name=None)
branch5x5 = Conv2d_BN(branch5x5,nb_filter,(1,1), padding=‘same‘,strides=(1,1),name=None)
branchpool = MaxPooling2D(pool_size=(3,3),strides=(1,1),padding=‘same‘)(x)
branchpool = Conv2d_BN(branchpool,nb_filter,(1,1),padding=‘same‘,strides=(1,1),name=None)
x = concatenate([branch1x1,branch3x3,branch5x5,branchpool],axis=3)
return x
def GoogLeNet():
inpt = Input(shape=(224,224,3))
#padding = ‘same‘,填充为(步长-1)/2,还可以用ZeroPadding2D((3,3))
x = Conv2d_BN(inpt,64,(7,7),strides=(2,2),padding=‘same‘)
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding=‘same‘)(x)
x = Conv2d_BN(x,192,(3,3),strides=(1,1),padding=‘same‘)
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding=‘same‘)(x)
x = Inception(x,64)#256
x = Inception(x,120)#480
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding=‘same‘)(x)
x = Inception(x,128)#512
x = Inception(x,128)
x = Inception(x,128)
x = Inception(x,132)#528
x = Inception(x,208)#832
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding=‘same‘)(x)
x = Inception(x,208)
x = Inception(x,256)#1024
x = AveragePooling2D(pool_size=(7,7),strides=(7,7),padding=‘same‘)(x)
x = Dropout(0.4)(x)
x = Dense(1000,activation=‘relu‘)(x)
x = Dense(1000,activation=‘softmax‘)(x)
model = Model(inpt,x,name=‘inception‘)
return model里程碑式创新:ResNet
2015年何恺明推出的ResNet在ISLVRC和COCO上横扫所有选手,获得冠军。ResNet在网络结构上做了大创新,而不再是简单的堆积层数,ResNet在卷积神经网络的新思路,绝对是深度学习发展历程上里程碑式的事件。
闪光点:
- 层数非常深,已经超过百层
- 引入残差单元来解决退化问题
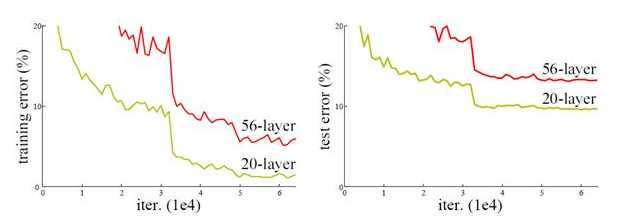
从前面可以看到,随着网络深度增加,网络的准确度应该同步增加,当然要注意过拟合问题。但是网络深度增加的一个问题在于这些增加的层是参数更新的信号,因为梯度是从后向前传播的,增加网络深度后,比较靠前的层梯度会很小。这意味着这些层基本上学习停滞了,这就是梯度消失问题。深度网络的第二个问题在于训练,当网络更深时意味着参数空间更大,优化问题变得更难,因此简单地去增加网络深度反而出现更高的训练误差,深层网络虽然收敛了,但网络却开始退化了,即增加网络层数却导致更大的误差,比如下图,一个56层的网络的性能却不如20层的性能好,这不是因为过拟合(训练集训练误差依然很高),这就是烦人的退化问题。残差网络ResNet设计一种残差模块让我们可以训练更深的网络。
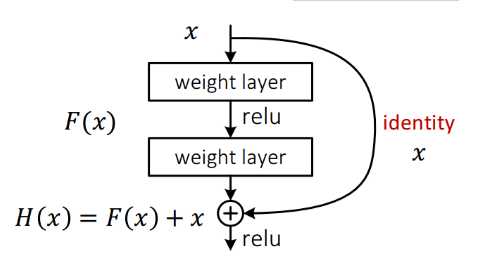
这里详细分析一下残差单元来理解ResNet的精髓。
从下图可以看出,数据经过了两条路线,一条是常规路线,另一条则是捷径(shortcut),直接实现单位映射的直接连接的路线,这有点类似与电路中的“短路”。通过实验,这种带有shortcut的结构确实可以很好地应对退化问题。我们把网络中的一个模块的输入和输出关系看作是y=H(x),那么直接通过梯度方法求H(x)就会遇到上面提到的退化问题,如果使用了这种带shortcut的结构,那么可变参数部分的优化目标就不再是H(x),若用F(x)来代表需要优化的部分的话,则H(x)=F(x)+x,也就是F(x)=H(x)-x。因为在单位映射的假设中y=x就相当于观测值,所以F(x)就对应着残差,因而叫残差网络。为啥要这样做,因为作者认为学习残差F(X)比直接学习H(X)简单!设想下,现在根据我们只需要去学习输入和输出的差值就可以了,绝对量变为相对量(H(x)-就是输出相对于输入变化了多少),优化起来简单很多。
考虑到x的维度与F(X)维度可能不匹配情况,需进行维度匹配。这里论文中采用两种方法解决这一问题(其实是三种,但通过实验发现第三种方法会使performance急剧下降,故不采用):
- zero_padding:对恒等层进行0填充的方式将维度补充完整。这种方法不会增加额外的参数
- projection:在恒等层采用1x1的卷积核来增加维度。这种方法会增加额外的参数
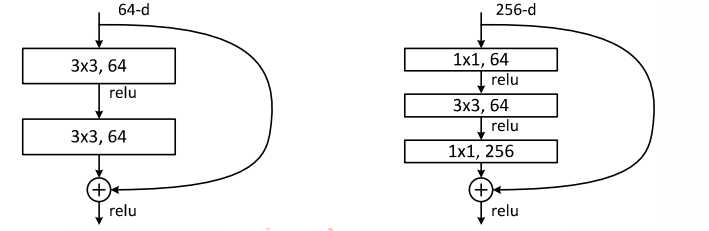
下图展示了两种形态的残差模块,左图是常规残差模块,有两个3×3卷积核卷积核组成,但是随着网络进一步加深,这种残差结构在实践中并不是十分有效。针对这问题,右图的“瓶颈残差模块”(bottleneck residual block)可以有更好的效果,它依次由1×1、3×3、1×1这三个卷积层堆积而成,这里的1×1的卷积能够起降维或升维的作用,从而令3×3的卷积可以在相对较低维度的输入上进行,以达到提高计算效率的目的。
ResNet-50的Keras实现:
def Conv2d_BN(x, nb_filter,kernel_size, strides=(1,1), padding=‘same‘,name=None):
if name is not None:
bn_name = name + ‘_bn‘
conv_name = name + ‘_conv‘
else:
bn_name = None
conv_name = None
x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation=‘relu‘,name=conv_name)(x)
x = BatchNormalization(axis=3,name=bn_name)(x)
return x
def Conv_Block(inpt,nb_filter,kernel_size,strides=(1,1), with_conv_shortcut=False):
x = Conv2d_BN(inpt,nb_filter=nb_filter[0],kernel_size=(1,1),strides=strides,padding=‘same‘)
x = Conv2d_BN(x, nb_filter=nb_filter[1], kernel_size=(3,3), padding=‘same‘)
x = Conv2d_BN(x, nb_filter=nb_filter[2], kernel_size=(1,1), padding=‘same‘)
if with_conv_shortcut:
shortcut = Conv2d_BN(inpt,nb_filter=nb_filter[2],strides=strides,kernel_size=kernel_size)
x = add([x,shortcut])
return x
else:
x = add([x,inpt])
return x
def ResNet50():
inpt = Input(shape=(224,224,3))
x = ZeroPadding2D((3,3))(inpt)
x = Conv2d_BN(x,nb_filter=64,kernel_size=(7,7),strides=(2,2),padding=‘valid‘)
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding=‘same‘)(x)
x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3),strides=(1,1),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3))
x = AveragePooling2D(pool_size=(7,7))(x)
x = Flatten()(x)
x = Dense(1000,activation=‘softmax‘)(x)
model = Model(inputs=inpt,outputs=x)
return model继往开来:DenseNet
自Resnet提出以后,ResNet的变种网络层出不穷,都各有其特点,网络性能也有一定的提升。本文介绍的最后一个网络是CVPR 2017最佳论文DenseNet,论文中提出的DenseNet(Dense Convolutional Network)主要还是和ResNet及Inception网络做对比,思想上有借鉴,但却是全新的结构,网络结构并不复杂,却非常有效,在CIFAR指标上全面超越ResNet。可以说DenseNet吸收了ResNet最精华的部分,并在此上做了更加创新的工作,使得网络性能进一步提升。
闪光点:
- 密集连接:缓解梯度消失问题,加强特征传播,鼓励特征复用,极大的减少了参数量
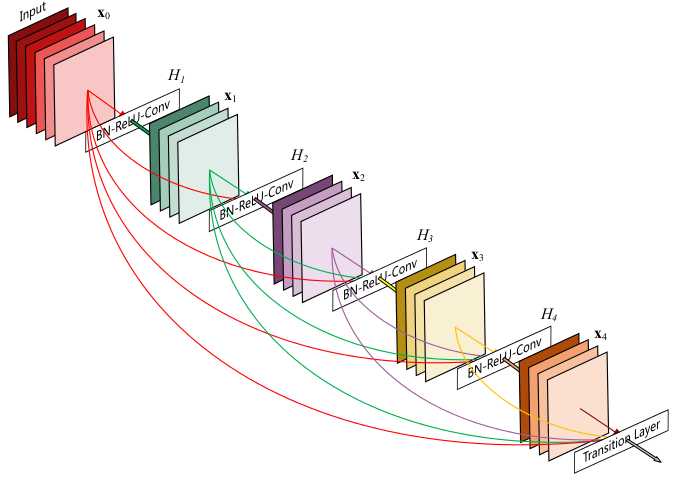
DenseNet 是一种具有密集连接的卷积神经网络。在该网络中,任何两层之间都有直接的连接,也就是说,网络每一层的输入都是前面所有层输出的并集,而该层所学习的特征图也会被直接传给其后面所有层作为输入。下图是 DenseNet 的一个dense block示意图,一个block里面的结构如下,与ResNet中的BottleNeck基本一致:BN-ReLU-Conv(1×1)-BN-ReLU-Conv(3×3) ,而一个DenseNet则由多个这种block组成。每个DenseBlock的之间层称为transition layers,由BN?>Conv(1×1)?>averagePooling(2×2)组成
密集连接不会带来冗余吗?不会!密集连接这个词给人的第一感觉就是极大的增加了网络的参数量和计算量。但实际上 DenseNet 比其他网络效率更高,其关键就在于网络每层计算量的减少以及特征的重复利用。DenseNet则是让l层的输入直接影响到之后的所有层,它的输出为:xl=Hl([X0,X1,…,xl?1]),其中[x0,x1,...,xl?1]就是将之前的feature map以通道的维度进行合并。并且由于每一层都包含之前所有层的输出信息,因此其只需要很少的特征图就够了,这也是为什么DneseNet的参数量较其他模型大大减少的原因。这种dense connection相当于每一层都直接连接input和loss,因此就可以减轻梯度消失现象,这样更深网络不是问题
需要明确一点,dense connectivity 仅仅是在一个dense block里的,不同dense block 之间是没有dense connectivity的,比如下图所示。

天底下没有免费的午餐,网络自然也不例外。在同层深度下获得更好的收敛率,自然是有额外代价的。其代价之一,就是其恐怖如斯的内存占用。
DenseNet-121的Keras实现:
def DenseNet121(nb_dense_block=4, growth_rate=32, nb_filter=64, reduction=0.0, dropout_rate=0.0, weight_decay=1e-4, classes=1000, weights_path=None):
‘‘‘Instantiate the DenseNet 121 architecture,
# Arguments
nb_dense_block: number of dense blocks to add to end
growth_rate: number of filters to add per dense block
nb_filter: initial number of filters
reduction: reduction factor of transition blocks.
dropout_rate: dropout rate
weight_decay: weight decay factor
classes: optional number of classes to classify images
weights_path: path to pre-trained weights
# Returns
A Keras model instance.
‘‘‘
eps = 1.1e-5
# compute compression factor
compression = 1.0 - reduction
# Handle Dimension Ordering for different backends
global concat_axis
if K.image_dim_ordering() == ‘tf‘:
concat_axis = 3
img_input = Input(shape=(224, 224, 3), name=‘data‘)
else:
concat_axis = 1
img_input = Input(shape=(3, 224, 224), name=‘data‘)
# From architecture for ImageNet (Table 1 in the paper)
nb_filter = 64
nb_layers = [6,12,24,16] # For DenseNet-121
# Initial convolution
x = ZeroPadding2D((3, 3), name=‘conv1_zeropadding‘)(img_input)
x = Convolution2D(nb_filter, 7, 7, subsample=(2, 2), name=‘conv1‘, bias=False)(x)
x = BatchNormalization(epsilon=eps, axis=concat_axis, name=‘conv1_bn‘)(x)
x = Scale(axis=concat_axis, name=‘conv1_scale‘)(x)
x = Activation(‘relu‘, name=‘relu1‘)(x)
x = ZeroPadding2D((1, 1), name=‘pool1_zeropadding‘)(x)
x = MaxPooling2D((3, 3), strides=(2, 2), name=‘pool1‘)(x)
# Add dense blocks
for block_idx in range(nb_dense_block - 1):
stage = block_idx+2
x, nb_filter = dense_block(x, stage, nb_layers[block_idx], nb_filter, growth_rate, dropout_rate=dropout_rate, weight_decay=weight_decay)
# Add transition_block
x = transition_block(x, stage, nb_filter, compression=compression, dropout_rate=dropout_rate, weight_decay=weight_decay)
nb_filter = int(nb_filter * compression)
final_stage = stage + 1
x, nb_filter = dense_block(x, final_stage, nb_layers[-1], nb_filter, growth_rate, dropout_rate=dropout_rate, weight_decay=weight_decay)
x = BatchNormalization(epsilon=eps, axis=concat_axis, name=‘conv‘+str(final_stage)+‘_blk_bn‘)(x)
x = Scale(axis=concat_axis, name=‘conv‘+str(final_stage)+‘_blk_scale‘)(x)
x = Activation(‘relu‘, name=‘relu‘+str(final_stage)+‘_blk‘)(x)
x = GlobalAveragePooling2D(name=‘pool‘+str(final_stage))(x)
x = Dense(classes, name=‘fc6‘)(x)
x = Activation(‘softmax‘, name=‘prob‘)(x)
model = Model(img_input, x, name=‘densenet‘)
if weights_path is not None:
model.load_weights(weights_path)
return model
def conv_block(x, stage, branch, nb_filter, dropout_rate=None, weight_decay=1e-4):
‘‘‘Apply BatchNorm, Relu, bottleneck 1x1 Conv2D, 3x3 Conv2D, and option dropout
# Arguments
x: input tensor
stage: index for dense block
branch: layer index within each dense block
nb_filter: number of filters
dropout_rate: dropout rate
weight_decay: weight decay factor
‘‘‘
eps = 1.1e-5
conv_name_base = ‘conv‘ + str(stage) + ‘_‘ + str(branch)
relu_name_base = ‘relu‘ + str(stage) + ‘_‘ + str(branch)
# 1x1 Convolution (Bottleneck layer)
inter_channel = nb_filter * 4
x = BatchNormalization(epsilon=eps, axis=concat_axis, name=conv_name_base+‘_x1_bn‘)(x)
x = Scale(axis=concat_axis, name=conv_name_base+‘_x1_scale‘)(x)
x = Activation(‘relu‘, name=relu_name_base+‘_x1‘)(x)
x = Convolution2D(inter_channel, 1, 1, name=conv_name_base+‘_x1‘, bias=False)(x)
if dropout_rate:
x = Dropout(dropout_rate)(x)
# 3x3 Convolution
x = BatchNormalization(epsilon=eps, axis=concat_axis, name=conv_name_base+‘_x2_bn‘)(x)
x = Scale(axis=concat_axis, name=conv_name_base+‘_x2_scale‘)(x)
x = Activation(‘relu‘, name=relu_name_base+‘_x2‘)(x)
x = ZeroPadding2D((1, 1), name=conv_name_base+‘_x2_zeropadding‘)(x)
x = Convolution2D(nb_filter, 3, 3, name=conv_name_base+‘_x2‘, bias=False)(x)
if dropout_rate:
x = Dropout(dropout_rate)(x)
return x
def transition_block(x, stage, nb_filter, compression=1.0, dropout_rate=None, weight_decay=1E-4):
‘‘‘ Apply BatchNorm, 1x1 Convolution, averagePooling, optional compression, dropout
# Arguments
x: input tensor
stage: index for dense block
nb_filter: number of filters
compression: calculated as 1 - reduction. Reduces the number of feature maps in the transition block.
dropout_rate: dropout rate
weight_decay: weight decay factor
‘‘‘
eps = 1.1e-5
conv_name_base = ‘conv‘ + str(stage) + ‘_blk‘
relu_name_base = ‘relu‘ + str(stage) + ‘_blk‘
pool_name_base = ‘pool‘ + str(stage)
x = BatchNormalization(epsilon=eps, axis=concat_axis, name=conv_name_base+‘_bn‘)(x)
x = Scale(axis=concat_axis, name=conv_name_base+‘_scale‘)(x)
x = Activation(‘relu‘, name=relu_name_base)(x)
x = Convolution2D(int(nb_filter * compression), 1, 1, name=conv_name_base, bias=False)(x)
if dropout_rate:
x = Dropout(dropout_rate)(x)
x = AveragePooling2D((2, 2), strides=(2, 2), name=pool_name_base)(x)
return x
def dense_block(x, stage, nb_layers, nb_filter, growth_rate, dropout_rate=None, weight_decay=1e-4, grow_nb_filters=True):
‘‘‘ Build a dense_block where the output of each conv_block is fed to subsequent ones
# Arguments
x: input tensor
stage: index for dense block
nb_layers: the number of layers of conv_block to append to the model.
nb_filter: number of filters
growth_rate: growth rate
dropout_rate: dropout rate
weight_decay: weight decay factor
grow_nb_filters: flag to decide to allow number of filters to grow
‘‘‘
eps = 1.1e-5
concat_feat = x
for i in range(nb_layers):
branch = i+1
x = conv_block(concat_feat, stage, branch, growth_rate, dropout_rate, weight_decay)
concat_feat = merge([concat_feat, x], mode=‘concat‘, concat_axis=concat_axis, name=‘concat_‘+str(stage)+‘_‘+str(branch))
if grow_nb_filters:
nb_filter += growth_rate
return concat_feat, nb_filter
