KMP算法
KMP算法的简介
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,简称KMP算法。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息,该算法时间复杂度为O(m+n)。
KMP算法的思路
例题:http://hihocoder.com/problemset/problem/1015

1 #include<cstdio> 2 #include<cstring> 3 using namespace std; 4 int n,l1,l2,j,ans; 5 char s1[1000001],s2[1000001]; 6 int main() 7 { 8 scanf("%d",&n); 9 while (n--) 10 { 11 scanf("%s%s",s2,s1); 12 l1=strlen(s1); 13 l2=strlen(s2); 14 ans=0; 15 for (int i=0;i<=l1-l2;i++) 16 for (int j=0;j<l2;j++) 17 if (s1[i+j]!=s2[j])break; 18 else 19 if (j==l2-1)ans++; 20 printf("%d\n",ans); 21 } 22 }
对于这个程序,显然是无法通过的,所以我们要对这个程序进行优化!模拟过程,我们可以发现一个浪费时间的地方: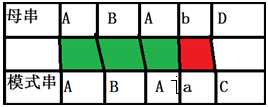
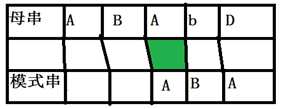
其中大写字母表示一段字符串,小写字母表示字符,此图中A为0-i最长相同前后缀,即不存在一个大于等于len(A)的k使得s2[0..k]==s2[i-k+1..i],我们设这个next[i]表示从0到i-1的相同前后缀的长度,这是需要与处理的。可以证明A必然可以如图2跳到该位置,具体证明详见后面。
KMP算法的过程
用i表示母串中匹配到第i个位置,子串中匹配到第j个位置,若s1[i]==s2[j]或j为0,i++,j++;反之则令j=next[j],继续进行判断(解释一下:相同显然要继续往下匹配,j就变成next[j],相当于做了后移操作)。
KMP算法预处理
KMP算法需要预处理next数组,暴力预处理时间复杂度需要n^2,显然不行。所以我们算next[i]要利用前面的next[j],所以我们假设前面的next都已经算好了,则若s[i-1]==s[next[i-1]],next[i]=next[i-1]+1;不同若s[i-1]==s[next[next[i-1]]],则next[i]=next[next[i-1]]+1;不同若s[i-1]==s[next[next[next[i-1]]]]……直到求出next[i]或者变成了0。
KMP算法的程序

1 #include<cstdio> 2 int n,l1,l2,ans,nex[10001]; 3 char s1[1000001],s2[10001]; 4 int calc(char *s,int k,char c) 5 { 6 for (;(k)&&(c!=s[k]);k=nex[k]); 7 return k+=(s[k]==c); 8 } 9 char seek(char *s) 10 { 11 nex[0]=nex[1]=0; 12 for (int i=1,j=0;s[i];i++)nex[i+1]=j=calc(s,j,s[i]); 13 } 14 void kmp(char *s1,char *s2) 15 { 16 for (int i=0,j=0;s1[i];i++) 17 if (!s2[j=calc(s2,j,s1[i])]) 18 { 19 ans++; 20 j=nex[j]; 21 } 22 } 23 int main() 24 { 25 scanf("%d",&n); 26 while (n--) 27 { 28 scanf("%s%s",s2,s1); 29 seek(s2); 30 ans=0; 31 kmp(s1,s2); 32 printf("%d\n",ans); 33 } 34 }

