感谢某位不知名dalao的博客,我才知道怎么解题....
最开始连题意都读错了....这个故事告诉我们要好好读题
描述 Description
图G是一个无向连通图,没有自环,并且两点之间至多只有一条边。我们定义顶点v,u最短路径就是从v到u经过边最少的路径。所有包含在v-u的最短路径上的顶点被称为v-u的Geodetic顶点,这些顶点的集合记作I(v, u)。
我们称集合I(v, u)为一个Geodetic集合。
例如下图中,I(2, 5)={2, 3, 4, 5},I(1, 5)={1, 3, 5},I(2, 4)={2, 4}。
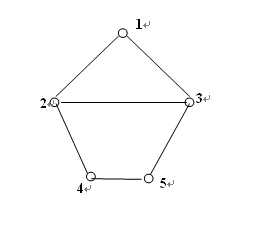
给定一个图G和若干点对v,u,请你分别求出I(v, u)。
输入格式 Input Format
第一行两个整数n,m,分别表示图G的顶点数和边数(顶点编号1-n)
下接m行,每行两个整数a,b表示顶点a和b之间有一条无向边。
第m+2行有一个整数k,表示给定的点对数。
下接k行,每行两个整数v,u。
输出格式 Output Format
共k行,每行对应输入文件中每一个点对v,u,按顶点编号升序输出I(v, u)。同一行的每个数之间用空格分隔。
样例输入 Sample Input
5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4
样例输出 Sample Output
2 3 4 5
1 3 5
2 4
思路挺简单,floyed一遍算出最短路径
然后再循环判断并记录集合内的点即可,然而实现看起来挺鬼畜!?感谢数据量不大吧.....
#include<bits/stdc++.h>
#define maxn 100
using namespace std;
struct node{
int x,y;
}a[10086];
int n,m,kk;
int fu[maxn][maxn],s[maxn][maxn];
int dis[maxn][maxn][maxn];
int main(){
cin>>n>>m;
memset(fu,10,sizeof(fu));
for(int i=1;i<=n;i++)
fu[i][i]=0;
for(int i=1;i<=m;i++){
int xx,yy;
cin>>xx>>yy;
fu[xx][yy]=1;fu[yy][xx]=1;
}
cin>>kk;
for(int i=1;i<=kk;i++){
cin>>a[i].x>>a[i].y;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(fu[i][k]+fu[k][j]<fu[i][j])//floyed求最短路
fu[i][j]=fu[i][k]+fu[k][j];
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(fu[i][k]+fu[k][j]==fu[i][j])//因为已经完成松弛,所以如果得出如此条件判断,说明是最短路径
dis[i][j][++s[i][j]]=k;//i,j固定位置,数组s[i][j]记录经过点的个数,dis数组存储顶点
for(int i=1;i<=kk;i++){
for(int j=1;j<=s[a[i].x][a[i].y];j++)//枚举集合内的点的个数
cout<<dis[a[i].x][a[i].y][j]<<‘ ‘;
cout<<endl;
}
return 0;
}
