归并排序算法实现:
#include<stdio.h>
#include<stdlib.h>
#define FatalError( Str ) fprintf( stderr, "%s\n", Str ), exit( 1 )
typedef int ElementType;
void Merge(ElementType A[],ElementType TmpArray[],int lpos,int rpos,int rightend)
{
int i,leftend,NumElements,TmpPos;
leftend=rpos-1;
TmpPos=lpos;
NumElements=rightend-lpos+1;
while(lpos<=leftend&&rpos<=rightend)
{
if(A[lpos]<=A[rpos])
TmpArray[TmpPos++]=A[lpos++];
else
TmpArray[TmpPos++]=A[rpos++];
}
while(lpos<=leftend)
TmpArray[TmpPos++]=A[lpos++];
while(rpos<=rightend)
TmpArray[TmpPos++]=A[rpos++];
//由于每次将临时数组中的元素复制回原来数组时,不能从第一个开始复制,只是从刚刚合并的那一部分复制,所以记录要合并的长度
for(i=0;i<NumElements;i++,rightend--)
A[rightend]=TmpArray[rightend];
}
void Msort(ElementType A[],ElementType TmpArray[],int left,int right)
{
int Center;
if(left<right)
{
Center=(left+right)/2;
Msort(A,TmpArray,left,Center);
Msort(A,TmpArray,Center+1,right);
Merge(A,TmpArray,left,Center+1,right);
}
}
void MergeSort(ElementType A[],int N)
{
ElementType *TmpArray;
TmpArray=malloc(sizeof(ElementType)*N);
if(TmpArray!=NULL)
{
Msort(A,TmpArray,0,N-1);
free(TmpArray);
}
else
FatalError("No space for tmp array[]");
}
void Print(int A[],int N)
{
int i;
for(i=0;i<N;i++)
printf(" %d ",A[i]);
}
int main()
{
int arr[10]={2,87,39,49,34,62,53,6,44,98};
Print(arr,10);
printf("\n");
MergeSort(arr,10);
Print(arr,10);
printf("\n");
return 0;
}
运行结果如下:
快速排序算法-C语言实现
注:本篇内容为翻译,之所以选择这篇进行翻译原因是该文章含有动画,能够更加直观地展示快速排序。同时,可以仔细看一下代码,代码中把结构化的思想给予了更加充分地表现。按照功能进行模块划分的思想得到了彻底地贯彻。
以下内容翻译自:
- http://cprogramminglanguage.net/quicksort-algorithm-c-source-code.aspx
译文:
在快速排序算法中,使用了分治策略。首先把序列分成两个子序列,递归地对子序列进行排序,直到整个序列排序结束。
步骤如下:
在序列中选择一个关键元素做为轴;
对序列进行重新排序,将比轴小的元素移到轴的前边,比轴大的元素移动到轴的后面。在进行划分之后,轴便在它最终的位置上;
递归地对两个子序列进行重新排序:含有较小元素的子序列和含有较大元素的子序列。
下面的动画展示了快速排序算法的工作原理。
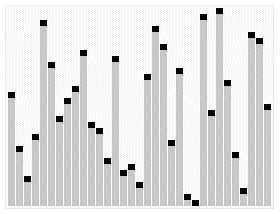
快速排序图示:可以图中在每次的比较选取的key元素为序列最后的元素。
#include <stdio.h>
#include <stdlib.h>
void swap(int *x,int *y)
{
int temp;
temp = *x;
*x = *y;
*y = temp;
}
int choose_pivot(int i,int j )
{
return((i+j) /2);
}
void quicksort(int list[],int m,int n)
{
int key,i,j,k;
if( m < n)
{
k = choose_pivot(m,n);
swap(&list[m],&list[k]);
key = list[m];
i = m+1;
j = n;
while(i <= j)
{
while((i <= n) && (list[i] <= key))
i++;
while((j >= m) && (list[j] > key))
j--;
if( i < j)
swap(&list[i],&list[j]);
}
// 交换两个元素的位置
swap(&list[m],&list[j]);
// 递归地对较小的数据序列进行排序
quicksort(list,m,j-1);
quicksort(list,j+1,n);
}
}
void printlist(int list[],int n)
{
int i;
for(i=0;i<n;i++)
printf("%d\t",list[i]);
}
void main()
{
const int MAX_ELEMENTS = 10;
int list[MAX_ELEMENTS];
int i = 0;
// 产生填充序列的随机数
for(i = 0; i < MAX_ELEMENTS; i++ ){
list[i] = rand();
}
printf("进行排序之前的序列:\n");
printlist(list,MAX_ELEMENTS);
// sort the list using quicksort
quicksort(list,0,MAX_ELEMENTS-1);
// print the result
printf("使用快速排序算法进行排序之后的序列:\n");
printlist(list,MAX_ELEMENTS);
}
改进版的快速排序
#include<stdio.h>
#include<stdlib.h>
typedef int ElementType;
#define Cutoff (3)
void swap(int *a,int *b)
{
int temp=*a;
*a=*b;
*b=temp;
}
void WithSentrySort(ElementType A[],int N)
{
int i,j;
for(i=2;i<N;i++)
{
A[0]=A[i];
for(j=i-1;A[j]>A[0];j--)
{
A[j+1]=A[j];
}
A[j+1]=A[0];
}
}
ElementType Median3(ElementType A[], int Left, int Right)
{
int Center = (Left + Right) / 2;
if (A[Left] > A[Center])
swap(&A[Left], &A[Center]);
if (A[Left] > A[Right])
swap(&A[Left], &A[Right]);
if (A[Center] > A[Right])
swap(&A[Center], &A[Right]);
swap(&A[Center], &A[Right - 1]);
return A[Right - 1];
}
void QSort(ElementType A[], int Left, int Right)
{
int i, j;
ElementType Pivot;
if (Left + Cutoff <= Right){
Pivot = Median3(A, Left, Right);
i = Left; j = Right - 1;
for (;;){
while (A[++i] < Pivot);
while (A[--j] > Pivot);
if (i < j)
swap(&A[i], &A[j]);
else
break;
}
swap(&A[i], &A[Right - 1]);
QSort(A, Left, i - 1);
QSort(A, i + 1, Right);
}
else
WithSentrySort(A + Left, Right - Left + 1);
}
void QuickSort(ElementType A[], int N)
{
QSort(A, 0, N -1);
}
void Print(int A[],int n)
{
int i;
for(i=0;i<n;i++)
printf("%d ",A[i]);
printf("\n");
}
int main()
{
const int MAX_ELEMENTS=10;
int list[MAX_ELEMENTS];
int i=0;
for(i=0;i<MAX_ELEMENTS;i++)
list[i]=rand();
printf("排序之前:");
Print(list,MAX_ELEMENTS);
QuickSort(list,MAX_ELEMENTS);
printf("排序之后:");
Print(list,MAX_ELEMENTS);
return 0;
}
运行结果:
不相交集(The Disjoint Set ADT)
0)引论
不相交集是解决等价问题的一种有效的数据结构,之所以称之为有效是因为,这个数据结构简单(几行代码,一个简单数组就可以搞定),快速(每个操作基本上可以在常数平均时间内搞定)。
首先我们要明白什么叫做等价关系,而在这个之前要先有一个关系(relation)的定义
Relation:定义在数据集S上的关系R是指,对于属于数据集S中的每一对元素(a,b),a R b要么是真要么是假。如果a R b为真,就说a related b,即a与b相关。
等价关系也是一种关系(Relation),只不过是要满足一些约束条件
a) a R a,对于所有属于S的a
b) a R b 当且仅当 b R a
c) a R b 并且 b R a 意味着 a R c
动态等价性问题:
定义在非空集合S上的关系R,对于任意属于数据集S中的每一对元素(a,b),确定a R b是否为真,也就是说a与b是否有关系。
而对于a与b是否有关系,我们只需要证明a与b是否在同一个等价类集合中。
1)基本结构
Find操作:返回给定元素的集合的名字,也就是检查a,b是否在同一个等价类中。对于Find运算,最重要的是判断Find(a,S) == Find(b,S)是否成立。
Union操作:如果a,b不在一个等价类中,可以用Union操作把这连个等价类合并为一个等价类。
我们可以用tree结构来表示一个集合,root可以表示集合的名字。由于仅有上面的两个操作而没有顺序信息,因此我们可以将所有的元素用1-N编号,编号可以用hashing方法。
进一步可以发现对于这两个操作无法使其同时达到最优,也就是说当Find以常数最坏时间运行时,Union操作会很慢,同理颠倒过来。因此就有了2种实现方式。
a)使Find运行快
在数组中保存每个元素的等价类的名字,将所有等价类的元素放到一个链表中
b)使Union运行快
使用树来表示每一个集合,根节点表示集合的名字。数组元素P[i]表示元素i的父亲,若i为root,则P[i]=0。
对于Union操作,相当于把连个树合并,也就是指针的移动,如下图所示:
typedef int DisjSet[NumSets+1];
typedef int SetType;
void initialize(DisjSet S)
{
int i;
for(i=NumSets;i>0;i--)
s[i]=0;
}
void SetUnion(DisjSet S, SetType Root1, SetType Root2)
{
S[Root2] = Root1;
}
SetType Find(ElementType X, DisjSet S)
{
if(S[x]<=0)
return x;
else
return Find(S[x],S);
}
对于Find操作就是一个不断返回父节点知道找到根节点的递归过程。
2)灵巧合并算法
上面的合并算法相当随意,它就是把第二棵树作为第一棵树的子树来完成合并操作。有一个简单的改进方法是总是让较小的树成为较大的树的子树,这种方法叫做Union-by-Size,如下图所示Union-by-Size可以降低树的深度,每个节点的深度都不会超过O(logN)。
为了实现这种方法,必须记录每一棵树的大小。我们可以另每一个根节点的数组元素表示树的大小的赋值,非根节点不变,依旧表示其父节点。这其实是把上面方法的数组中的0的位置做了一些利用。
另一种方法是Union-by-Height,也就是说我们把高度较浅的树作为高度较深的树的子树。亦即根节点记录的是树的高度的负值。
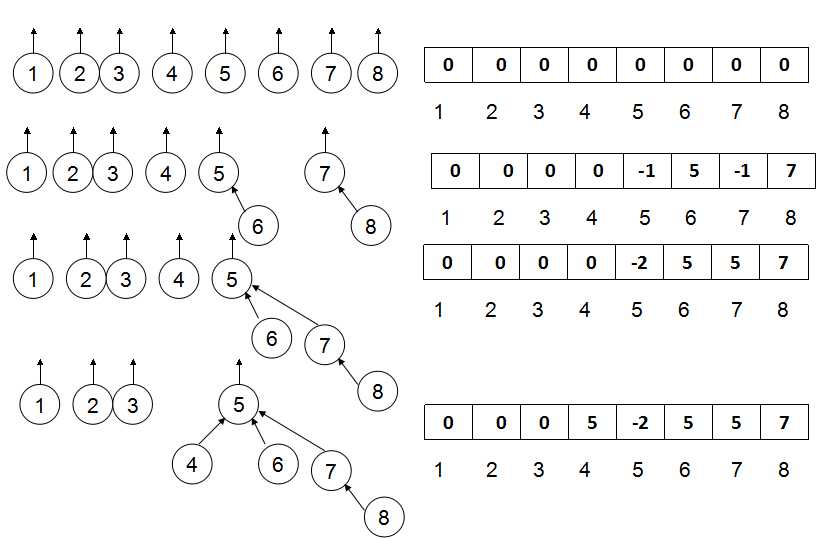
Union-by-Height的Union代码实现
void SetUnion(DisjSet S, SetType Root1, SetType Root2)
{
//add the low height tree to the high height tree.
if(S[Root2]<S[Root1])
S[Root1] = Root2;
else
{
if(S[Root1] = S[Root2]) //same height
S[Root1]--;
S[Root2] = Root1;
}
}
3)路径压缩
随着树的加深,Find操作的时间会增加。如果Find操作比Union操作多的多的话,那么运算时间会相当糟糕,比快速查找还要差。而且从上面可以看出,Union算法的改进比较困难,因此我们应该尝试去使Find更加高效。这就引入了path compression。
路径压缩:在Find操作期间执行与Union操作无关,路径压缩的效果是从X到根节点的路径上的每一个结点都使它的父节点成为根节点。
代码实现:
SetType Find(ElementType X, DisjSet S)
{
if(S[x]<=0)
return x;
else
return S[x] = Find(S[x],S);
}
和上面相比,代码只有一点点小修改。
路径压缩算法是与Union-by-Size相兼容的,与Union-by-Height并不完全兼容。
4)小应用
说了这么多,这个数据结构总要有点用处啊,否则就没有什么意义了。
一个例子是计算机网络和双向连接表,每一个连接将文件从一个计算机传递到另一个计算机。现在的问题是能否将文件从任意一个计算机传递到另一个任意的计算机,并且这个问题要on-line解决。
解决这个问题,就可以用到上面的数据结构。开始阶段我们可以把每一台计算机放到他自己的集合中,要求两台计算机传递文件当且仅当这两台计算机在同一个集合中。因此传输文件能力相当于一个等价关系。当我们需要传输文件时,检验两个计算机是否在同一个集合里,是的话就传输文件,否的话,就用Union方法把它们合并到一个集合中,然后传输文件。
5)总结
不相交集是一个非常简单的数据结构,仅用几行代码就可以搞定。对于Find操作,重要的是Find(a,S) == Find(b,S)为真还是假。Union操作有很多种实现,比较灵活。为了节省Find操作的时间,引入了路径压缩算法,这是自调整(self-adjustment)的最早形式之一。




















