1.定义:
回溯算法是一种在穷举查找基础上的增强变形。主要是在尝试搜索的过程中,每次只构造解的一个分量,当发现部分构造解满足求解条件时,就接受下一个分量所做的第一个合法选择;当发现部分构造解不满足求解条件时,就回溯返回,尝试另外的路径。这种走不通就回头的算法称为回溯算法。
主要思想:通过对所做的选择构造一颗状态空间树,按照深度优先的策略,从根开始深度搜索状态空间树。当搜索到某一结点,先判断该节点是否可以构成完整解,如果可以就继续向下搜索;否则就逐层返回回溯,尝试其他路径。(隐式图的深度优先搜索)
核心思想:个人以为,回溯法的核心是状态空间树的构造(可能是隐式构造的),一旦确立了状态空间树,就可以直接得出问题的解。状态空间树的构造思想是:按照深度优先的方式,如果当前节点的下一个分量所构造的部分解可以导致完整解,就生成节点的子女,并添加下一个分量的第一个合法选择;否则就回溯到该节点的父母,考虑部分解的下一个分量选择。
2.回溯算法的一般步骤(解决某些约束下的最优解):
(1)确定问题的解空间(包含所有解的一颗状态空间树),确定完全解的形式,以及部分构造解无法构成完全解的剪枝规则。( ps:问题的解空间(状态空间树)是在DFS的过程中动态生成的)
(2)确定节点(分量)的扩展规则,即下一个节点的选择规则。 (ps:如曼哈顿问题中,按照字母顺序选择下一个分量)
(3)以深度优先的方式搜索解空间,并在搜索的过程中用剪枝函数判断该节点是否可以生成完全解。如果可以,则进入该节点的子树下一步搜索(构造下一个分量);如果不能,则跳过该节点的子树(不再生成下一个分量),逐层回溯。(ps:剪枝函数包括约束函数和界限函数,分别剪去不满足约束的节点和不能得到最优解的函数)
3.回溯的算法框架:
(1)递归的方式:
int x[n]; void backtrack(int t) { if(t>n) //到达叶子节点,输出结果,x是可行解 output(x); else { for i = 1 to k //该节点的子节点(分量的所有下一个分量) { x[t] = value(i); //取出子节点的值 if(constraint(t) && bount(t) ) //剪枝函数:判断约束和界限 backtrack(t+1); //可以生成完全解,继续递归下去 } } }
特点:思路简单,设计简单,但算法时间效率很差。
(2)递推的方式:
void backtrack() { int t=1; while(t>0) { if(existSubNode(t)) //存在子节点:该结点还有可以构造的节点(下一个分量) { for i = 1 to k { x[t] = value(i); //相当于在此处建立一个结点 if(constraint(t) && bount(t) ) //剪枝函数判断约束和界限 { if(isResult(t) ) //得到了一个结果,输出 output(x); else //还没有得到结果,继续向下搜索 t++; } else { eraseSubNode(t) //该结点无法构成完全解,故删去该结点,并设该结点不可再作为子节点。 } } } else { eraseSubNode(t); //该结点没有子结点,也不能完全解,所以删去该结点。 t--; //进行回溯 } } }
特点:设计复杂,但算法时间效率很高。
4.用回溯的思想实现背包问题:
用回溯算法解决01背包问题,步骤:
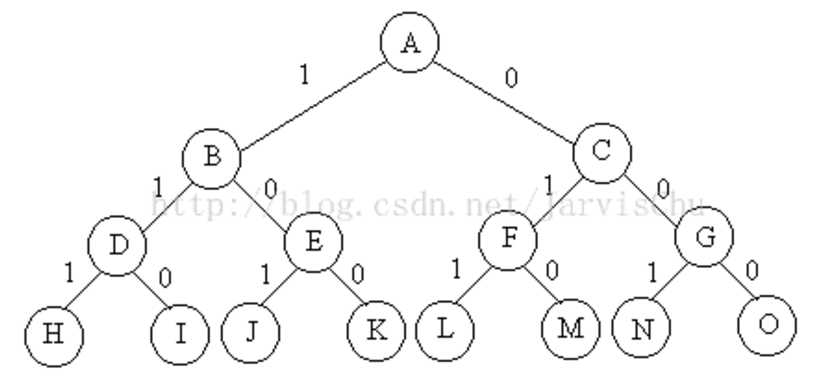
(1)问题的解空间是子集树,节点表示前 t 个物品的存放状态,树枝的值表示第 t 个物品有没有放入背包。完全解的形式是01组成的N个数,避免无法构造完全解的约束剪枝规则是:当前背包的物品重量CurWeight加新增的物品重量不能超过背包的承重C(CurWeight+w[t]<C)。
当物品数为3时,解空间(状态空间树)如下:

(2)节点扩展规则:数字递增顺序,也就是说第t个物品放入背包和没有放入背包的状态,即 0 和 1.
(3)回溯搜索:如果搜索到叶子节点,表示一条路径搜索结束,如果存在更优解则记录。
如果没有搜索到叶子节点,则遍历其子节点,满足剪枝条件时继续向下搜索,不满足时回溯。
#include <iostream> using namespace std; #define N 4 //物品总数 #define C 5 //背包的承重 int w[N] = {2,1,3,2}; //物品重量 int v[N] = {12,10,20,15}; //物品价值 int CurWeight = 0; //当前总重量 int CurValue = 0; //当前总价值 int x[N] ={0,0,0}; //当前的背包选取情况(1表示选取,0表示不选取) int MaxValue = 0; //最大价值 int MaxPack[N] = {0,0,0}; //最大价值下的背包选取情况(1表示选取,0表示不选取) void backtrack(int t) { if(t >= N) //到达叶子处,说明已经求得一个满足约束的完全解,接下来判断是否最优 { if(CurValue > MaxValue) { MaxValue = CurValue; for(int i=0;i<N;i++) MaxPack[i] = x[i]; } } else //没到叶子处,还要继续向下搜索下去 { for(int i=0;i<=1;i++) { x[t] = i; //01背包问题中,每个物品的存放状态是 0 或 1。此处表示第 t 个物品在背包中的状态为 0 或 1。 if(x[t] == 0) //第 t 个物品没有放入背包,不进行剪枝判断 { backtrack(t+1); } else //第 t 个物品放入背包,要进行剪枝判断 { if(CurWeight + w[t] <= C) //剪枝判断为满足约束条件 { CurWeight += w[t]; //当前结点满足约束,则增加结点的值到当前值中 CurValue += v[t]; backtrack(t+1); //继续向下搜索 CurWeight -= w[t]; //为了回溯到父节点的状态,要将子节点新增的内容删掉 CurValue -= v[t]; } } } } } int main() { backtrack(0); cout<<"the max value pack combination: "; for(int i=0; i<N; i++) cout<<MaxPack[i]<<" "; cout<<"\nthe max value: "<<MaxValue<<endl; }
