最近在用Java刷剑指offer(第二版)的面试题。书中原题的代码采用C++编写,有些题的初衷是为了考察C++的指针、模板等特性,这些题使用Java编写有些不合适。但多数题还是考察通用的算法、数据结构以及编程思想等,与语言本身无太大关系。因此在选择编程语言时,我还是选择了Java。好吧,主要是我C++不怎么会,仅仅是曾经学过俩月,使用Java顺手一些。后续可能再用Python刷一遍。
面试题3 数组中重复的数字
题目一:找出数组中重复的数字
- 描述:在长度为n的数组里所有数字都在0~n-1范围内。数组中某些数字是重复的,请找出任意一个重复的数字。如数组{2, 3, 1, 0, 2, 5, 3},输出的重复的数字为2或3。
- 思路:利用数组的索引在0~n-1这个范围的性质,将数字i移至索引i的位置。
- 考点:对数组的理解以及对问题的分析能力。
题目二:不修改数组找出重复的数字
- 描述:在长度为n+1的数组里所有数字都在1~n范围内。找出重复的数字,但不修改数组。
- 思路:当然可完全利用题目一的方法,只是需要辅助空间。不需要辅助空间是最好的了。这里使用二分法,对数组进行计数,逐渐缩小重复的数字所处的范围。
- 考点:对二分查找的灵活应用,毕竟写出正确无误的二分法时有些难度的。同时要重视与面试官的沟通,明确需求,如是否能更改数组,是否可以使用辅助空间等。
package sword_offer; //page 39 数组中重复的数字 public class Solution3 { //题目1 //输出数组中重复的数字,空间复杂度O(1),时间复杂度O(n) //数组长度为n,数字在0~n-1范围内 public static int duplicate(int[] arr) { for (int i = 0; i < arr.length; i++) { //System.out.println(i); while (arr[i] != i) { if (arr[i] == arr[arr[i]]) return arr[i]; else { int temp = arr[i]; arr[i] = arr[temp]; arr[temp] = temp; //System.out.println(Arrays.toString(arr)); } } } return -1; } //题目2 //输出数组中重复的数字,空间复杂度O(1),时间复杂度O(nlog(n)) //数组长度为n+1,数字在1~n范围内,要求不修改数组,并不使用辅助空间 public static int myGetDuplication(int[] arr) { int start = 1; int middle = arr.length / 2; int end = middle; while(end >= start) { //System.out.println("" + start + end); int count = 0; for (int i = 0; i < arr.length; i++) { if (arr[i] >= start && arr[i] <= end) count++; } if (end == start) { if (count > 1) return start; else break; } if (count > end - start + 1) { middle = (start + end) / 2; end = middle; } else { start = middle + 1; end = arr.length - 1; } } return -1; } //输出数组中重复的数字,空间复杂度O(1),时间复杂度O(nlog(n)) //数组长度为n+1,数字在1~n范围内,要求不修改数组,并不使用辅助空间 //比上一个函数逻辑清晰一点 public static int getDuplication(int[] arr) { int start = 1; int end = arr.length - 1; while(end >= start) { int middle = (end - start) / 2 + start; int count = getCount(arr, start, middle); if (end == start) { if (count > 1) return start; else break; } if (count > middle - start + 1) { end = middle; } else start = middle + 1; } return -1; } //计算数组arr元素处在[start, end]范围内元素个数 private static int getCount(int[] arr, int start, int end) { int count = 0; for (int i = 0; i < arr.length; i++) { if (arr[i] >= start && arr[i] <= end) count++; } return count; } //测试 public static void main(String[] args) { int[] arr = {1, 2, 3, 1}; System.out.println(duplicate(arr)); int[] arr2 = {2, 3, 5, 4, 3, 2, 6, 7}; System.out.println(myGetDuplication(arr2)); int[] arr3 = {2, 3, 5, 4, 3, 2, 6, 7}; System.out.println(getDuplication(arr3)); } }
面试题4 二维数组中的查找
- 描述:二维数组中,数字按从左到右、从上到下的顺序递增。给定一个整数,判断该数组中是否含有该整数。
- 思路:从数组的右上角或左下角开始进行查找数据,缩小可能包含该数的范围。
- 考点:画图分析问题,寻求问题的突破口。并能正确编写程序,避免死循环等问题。
例如,从二维数组$\left[ {\begin{array}{*{20}{c}}
{1}&{2}&{8}&9 \\
{1}&{4}&{9}&{12} \\
{4}&{7}&{10}&{13} \\
{6}&{8}&{11}&{15}
\end{array}} \right]$中寻找是否包含数字7。
从右上角查找时,逐渐向左下方缩小范围。红色的代表包含目标值7的区域,过程如下:
$$\left[ {\begin{array}{*{20}{c}}
{\color{red}1}&{\color{red}2}&{\color{red}8}&9 \\
{\color{red}1}&{\color{red}4}&{\color{red}9}&{12} \\
{\color{red}4}&{\color{red}7}&{\color{red}{10}}&{13} \\
{\color{red}6}&{\color{red}8}&{\color{red}{11}}&{15}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{\color{red}1}&{\color{red}2}&{8}&9 \\
{\color{red}1}&{\color{red}4}&{9}&{12} \\
{\color{red}4}&{\color{red}7}&{10}&{13} \\
{\color{red}6}&{\color{red}8}&{11}&{15}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{1}&{2}&{8}&9 \\
{\color{red}1}&{\color{red}4}&{9}&{12} \\
{\color{red}4}&{\color{red}7}&{10}&{13} \\
{\color{red}6}&{\color{red}8}&{11}&{15}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{1}&{2}&{8}&9 \\
{1}&{4}&{9}&{12} \\
{\color{red}4}&{\color{red}7}&{10}&{13} \\
{\color{red}6}&{\color{red}8}&{11}&{15}
\end{array}} \right]$$
从左下角查找时,逐渐向右上方缩小范围。过程如下:
$$\left[ {\begin{array}{*{20}{c}}
{1}&{\color{red}2}&{\color{red}8}&{\color{red}9} \\
{1}&{\color{red}4}&{\color{red}9}&{\color{red}{12}} \\
{4}&{\color{red}7}&{\color{red}{10}}&{\color{red}{13}} \\
{6}&{\color{red}8}&{\color{red}{11}}&{\color{red}{15}}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{1}&{\color{red}2}&{\color{red}8}&{\color{red}9} \\
{1}&{\color{red}4}&{\color{red}9}&{\color{red}{12}} \\
{4}&{\color{red}7}&{\color{red}{10}}&{\color{red}{13}} \\
{6}&{8}&{11}&{15}
\end{array}} \right]$$
package sword_offer; //page 44 二维数组中的查找 public class Solution4 { //从右上角的元素开始查找,逐渐缩小范围 public static boolean findNum(int[][] arr, int target) { boolean found = false; int row = 0; int col = arr[0].length - 1; while (col > 0 && row <= arr.length) { int diff = arr[row][col] - target; if (diff == 0) { found = true; break; } else if (diff > 0) col--; else row++; } return found; } //测试 public static void main(String[] args) { int[][] arr = {{1,2,8,9},{2,4,9,12},{4,7,10,13},{6,8,11,15}}; System.out.println(findNum(arr, 9)); } }
面试题5 替换空格
- 描述:将字符串中的每个空格替换成%20。如输入"we are fine",输出"we%20are%20fine"。
- 思路:原题考察了C++中指针的操作。Java里数组不可变,因此本题变得没有难度了。利用String对象的.charAt函数遍历每个字符,并使用StringBuilder构建新的字符串。
- 考点:对字符串的处理。
package sword_offer; //page 51 替换空格 public class Solution5 { //在Java中字符串时不可变的,因而只能构造一个新的字符串。原文中该题的难点也无法体现出来了。 public static String replaceBlank(String str) { StringBuilder strb = new StringBuilder(); for (int i = 0; i < str.length(); i++) { if (str.charAt(i) == ‘ ‘) { strb.append("%20"); } else strb.append(str.charAt(i)); } return strb.toString(); } //测试 public static void main(String[] args) { String str = "We are happr."; System.out.println(replaceBlank(str)); } }
面试题6 从尾到头打印链表
- 描述:输入一个链表的头节点,从尾到头打印每个节点的值。
- 思路:从尾到头打印,即为“先进后出”,则可以使用栈来处理;考虑递归的本质也是一个栈结构,可递归输出。
- 考点:对链表、栈、递归的理解。
package sword_offer; //page 58 从尾到头打印链表 import java.util.Stack; //链表类 class ListNode{ ListNode next = null; int value; } public class Solution6 { //方法1:使用Stack栈的先push后pop public static void printListReverse(ListNode listNode) { Stack<ListNode> stack = new Stack<ListNode>(); while(listNode != null) { stack.push(listNode); listNode = listNode.next; } while(!stack.isEmpty()) { System.out.println(stack.pop().value); } } //方法2:使用递归的方式,相当于从内部往外部推 public static void printListReverse_rec(ListNode listNode) { if(listNode != null) { if (listNode.next != null) printListReverse_rec(listNode.next); System.out.println(listNode.value); } } //测试 public static void main(String[] args) { ListNode ln1 = new ListNode(); ListNode ln2 = new ListNode(); ListNode ln3 = new ListNode(); ln1.next = ln2; ln2.next = ln3; ln1.value = 1; ln2.value = 2; ln3.value = 3; printListReverse_rec(ln1); printListReverse(ln1); } }
面试题7 重建二叉树
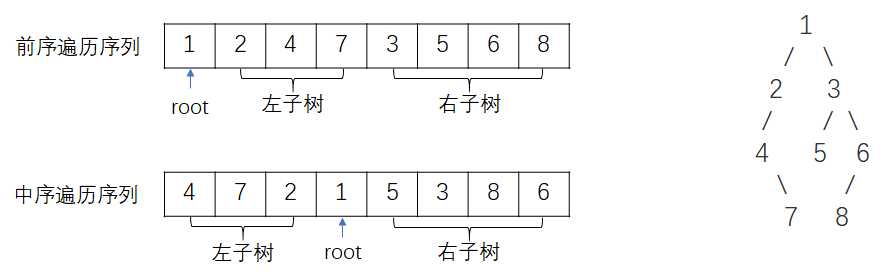
- 描述:输入某二叉树的前序遍历和中序遍历结果,重建该二叉树。假设前序遍历或中序遍历的结果中无重复的数字。
- 思路:前序遍历的第一个元素为根节点的值,据此将中序遍历数组拆分为左子树+root+右子树,前序遍历数组拆分为root+左子树+右子树。再对左右子树进行同样的操作。
- 考点:对二叉树不同遍历方法的掌握。
package sword_offer; //page 62 重建二叉树 //二叉树类,包含左右子树,以及用于查看的方法 class BinaryTreeNode { int value; BinaryTreeNode leftNode; BinaryTreeNode rightNode; //中序遍历输出查看 public void printList() { if (leftNode != null) leftNode.printList(); System.out.println(value); if (rightNode != null) rightNode.printList(); } } public class Solution7 { //重建二叉树函数 public static BinaryTreeNode rebultTree(int[] preorder, int[] inorder) { BinaryTreeNode root = rebultTree(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1); return root; } //重写函数 private static BinaryTreeNode rebultTree(int[] preorder, int startPre, int endPre, int[] inorder, int startIn, int endIn) { if (startPre > endPre || startIn > endIn) return null; BinaryTreeNode root = new BinaryTreeNode(); root.value = preorder[startPre]; for (int i = startIn; i <= endIn; i++) { if (inorder[i] == preorder[startPre]) { root.leftNode = rebultTree(preorder, startPre + 1, startPre + i - startIn, inorder, startIn, i - 1); root.rightNode = rebultTree(preorder, startPre + i - startIn + 1, endPre, inorder, i + 1, endIn); } } return root; } //测试 public static void main(String[] args) { int[] preorder = { 1, 2, 4, 7, 3, 5, 6, 8 }; int[] inorder = { 4, 7, 2, 1, 5, 3, 8, 6 }; BinaryTreeNode root = rebultTree(preorder, inorder); //System.out.println(root.leftNode.rightNode.value); root.printList(); } }
面试题8 二叉树的下一个节点
- 描述:给定一棵二叉树和其中的一个节点,找出中序遍历序列的下一个节点。树中应定义指向左节点、右节点、父节点的三个变量。
- 思路:该节点若存在右节点,右子树的最左节点则为下一节点;若不存在右节点,则向上遍历,直至找到是父节点的左节点的那个节点,该节点的父节点则为下一节点。
- 考点:对中序遍历的理解。
package sword_offer; //page 65 二叉树的下一个节点 //定义二叉树类,包含左右子树、父节点,以及用于查看的函数 class TreeNode { char value; TreeNode left; TreeNode right; TreeNode father; //中序遍历输出查看 public void printList() { if (left != null) left.printList(); System.out.println(value); if (right != null) right.printList(); } } public class Solution8 { public static TreeNode findNext(TreeNode node) { //有右节点,找到右子树的最左节点 if (node.right!= null) { node = node.right; while(node.left != null) node = node.left; return node; } //无右节点,则向上遍历,直至找到节点为父节点的左子节点 while(node.father != null) { if (node.father.left == node) return node.father; node = node.father; } return null; } public static void main(String[] args) { //建立一个二叉树节点的数组,并tree[i].value赋值 TreeNode[] tree = new TreeNode[9]; char[] chars = {‘a‘, ‘b‘, ‘c‘, ‘d‘, ‘e‘, ‘f‘, ‘g‘, ‘h‘, ‘i‘}; for (int i = 0; i < tree.length; i++) { tree[i] = new TreeNode(); tree[i].value = chars[i]; } /* * a * / * b c * / \ / * d e f g * / * h i */ //左右节点关系 tree[0].left = tree[1]; tree[0].right = tree[2]; tree[1].left = tree[3]; tree[1].right = tree[4]; tree[2].left = tree[5]; tree[2].right = tree[6]; tree[4].left = tree[7]; tree[4].right = tree[8]; //父节点关系 tree[1].father = tree[0]; tree[2].father = tree[0]; tree[3].father = tree[1]; tree[4].father = tree[1]; tree[5].father = tree[2]; tree[6].father = tree[2]; tree[7].father = tree[4]; tree[8].father = tree[4]; tree[0].printList(); } }
面试题9 两个栈实现队列
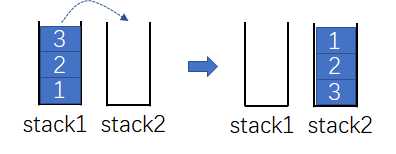
- 描述:使用两个栈实现一个队列。队列中实现尾部插入和头部删除函数。
- 思路:栈结构“先进后出”,插入数据时进入第一个栈;删除数据时,将第一个栈的所有数据都弹出到第二个栈,这时原先先插入的数据位于栈的顶端。即可满足队列的“先进先出”。
- 考点:对栈和队列的理解;对泛型的使用等。
package sword_offer; //page 68 两个栈实现队列 import java.util.Stack; //队列类,包含两个栈、两个操作队列的方法 class Queue <T>{ Stack<T> stack1 = new Stack<>(); Stack<T> stack2 = new Stack<>(); //插入节点 public void appendTail(T element) { stack1.push(element); } //删除节点 public T deleteHead(){ if (stack2.isEmpty()) { while(!stack1.isEmpty()) { T data = stack1.pop(); stack2.push(data); } } //为空时,输出异常 if (stack2.isEmpty()) throw new IllegalArgumentException("queue is empty"); return stack2.pop(); } } public class Solution9 { //测试 public static void main(String[] args) { Queue<Integer> queue = new Queue<>(); queue.appendTail(1); queue.appendTail(2); queue.appendTail(3); System.out.println(queue.deleteHead()); System.out.println(queue.deleteHead()); queue.appendTail(4); System.out.println(queue.deleteHead()); System.out.println(queue.deleteHead()); System.out.println(queue.deleteHead()); } }
