时间序列:可以用来预测未来的参数,
1.生成时间序列对象
1 sales <- c(18, 33, 41, 7, 34, 35, 24, 25, 24, 21, 25, 20, 2 22, 31, 40, 29, 25, 21, 22, 54, 31, 25, 26, 35) 3 # 1.生成时序对象 4 tsales <- ts(sales,start = c(2003,1),frequency = 12) 5 plot(tsales) 6 # 2.获得对象信息 7 start(tsales) 8 end(tsales) 9 frequency(tsales) 10 # 3.对相同取子集 11 tsales.subset <- window(tsales,start=c(2003,5),end=c(2004,6)) 12 tsales.subset
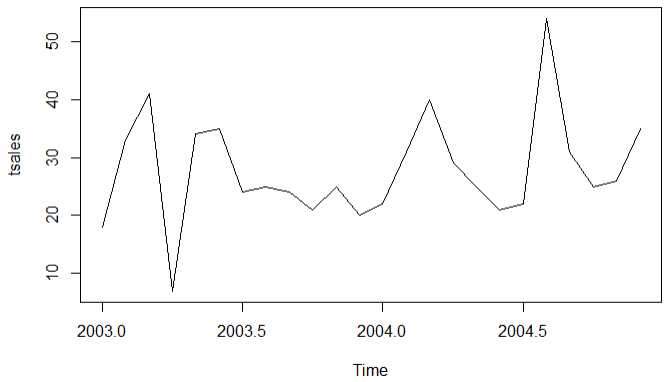
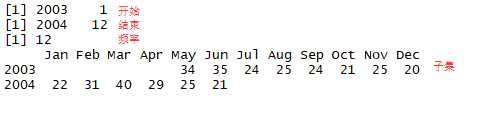
结论:手动生成的时序图
2.简单移动平均
案例:尼罗河流量和年份的关系
1 library(forecast) 2 opar <- par(no.readonly = T) 3 par(mfrow=c(2,2)) 4 ylim <- c(min(Nile),max(Nile)) 5 plot(Nile,main=‘Raw time series‘) 6 plot(ma(Nile,3),main = ‘Simple Moving Averages (k=3)‘,ylim = ylim) 7 plot(ma(Nile,7),main = ‘Simple Moving Averages (k=3)‘,ylim = ylim) 8 plot(ma(Nile,15),main = ‘Simple Moving Averages (k=3)‘,ylim = ylim) 9 par(opar)
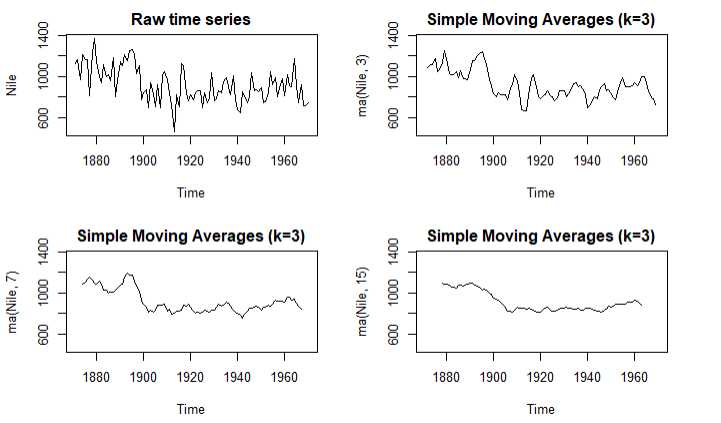
结论:随着K值的增大,图像越来越平滑我们需要找到最能反映规律的K值
3.使用stl做季节性分解
案例:Arirpassengers年份和乘客的关系
1 # 1.画出时间序列 2 plot(AirPassengers) 3 lAirpassengers <- log(AirPassengers) 4 plot(lAirpassengers,ylab = ‘log(Airpassengers)‘) 5 # 2.分解时间序列 6 fit <- stl(lAirpassengers,s.window = ‘period‘) 7 plot(fit) 8 fit$time.series 9 par(mfrow=c(2,1)) 10 # 3.月度图可视化 11 monthplot(AirPassengers,xlab=‘‘,ylab=‘‘) 12 # 4.季度图可视化 13 seasonplot(AirPassengers,year.labels = T,main = ‘‘)
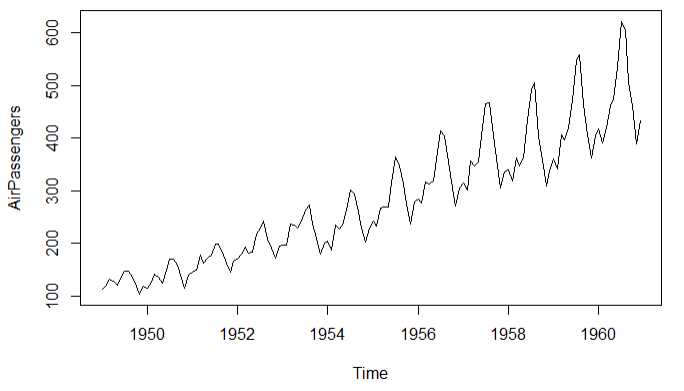
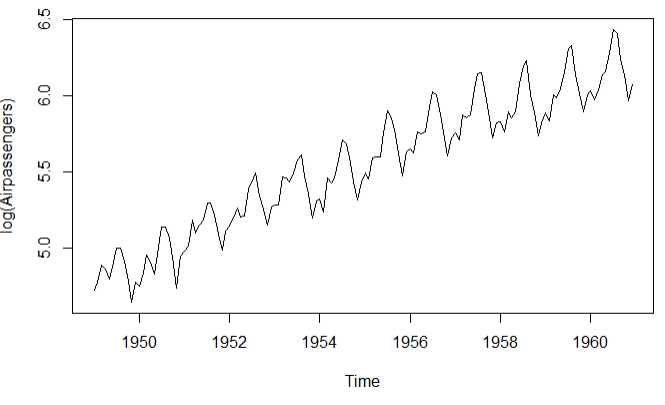
原始图 对数变换
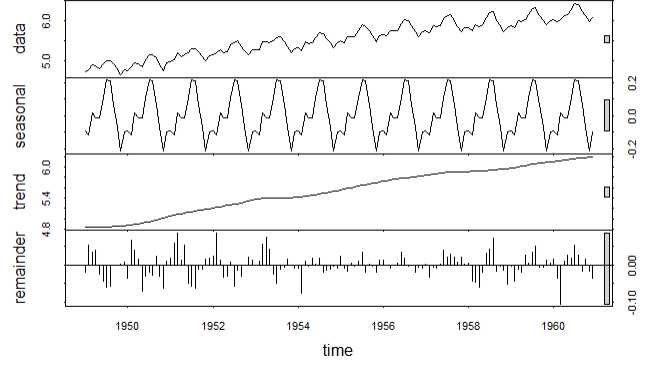
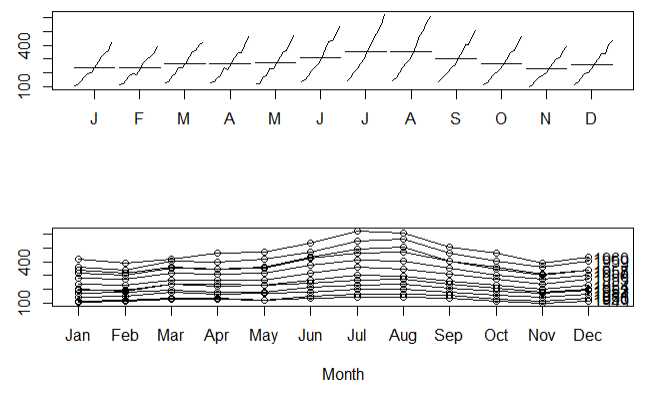
总体趋势图 月度季度图
4.指数预测模型
4.1单指数平滑
案例:预测康涅狄格州的气温变化
# 1.拟合模型 fit2 <- ets(nhtemp,model = ‘ANN‘) fit2 # 2.向前预测 forecast(fit2,1) plot(forecast(fit2,1),xlab = ‘Year‘, ylab = expression(paste("Temperature (",degree*F,")",)), main="New Haven Annual Mean Temperature") # 3.得到准确的度量 accuracy(fit2)
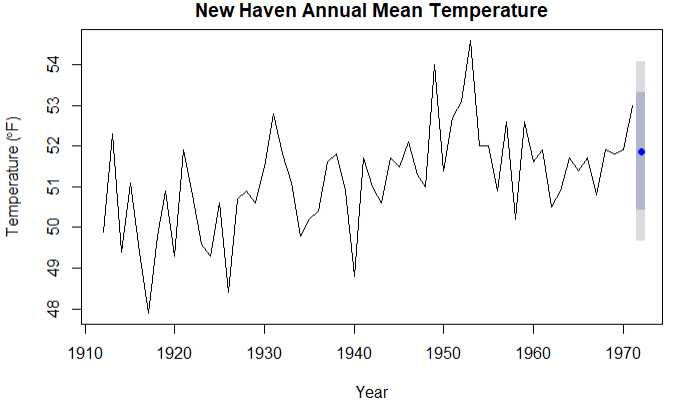
结论:浅灰色是80%的置信区间,深灰色是95%的置信区间
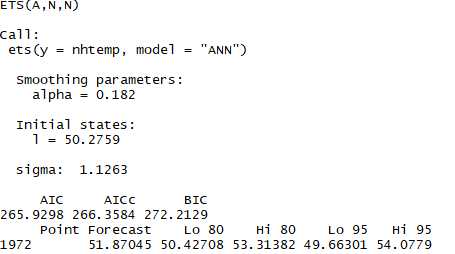
4.2有水平项,斜率和季节项的指数模型
案例:预测5个月的乘客流量
1 # 1.光滑参数 2 fit3 <- ets(log(AirPassengers),model = ‘AAA‘) 3 accuracy(fit3) 4 # 2.未来值预测 5 pred <- forecast(fit3,5) 6 pred 7 plot(pred,main=‘Forecast for air Travel‘,ylab = ‘Log(Airpassengers)‘,xlab = ‘Time‘) 8 # 3.使用原始尺度预测 9 pred$mean <- exp(pred$mean) 10 pred$lower <- exp(pred$lower) 11 pred$upper <- exp(pred$upper) 12 p <- cbind(pred$mean,pred$lower,pred$upper) 13 dimnames(p)[[2]] <- c(‘mean‘,‘Lo 80‘,‘Lo 95‘,‘Hi 80‘,‘Hi 95‘) 14 p
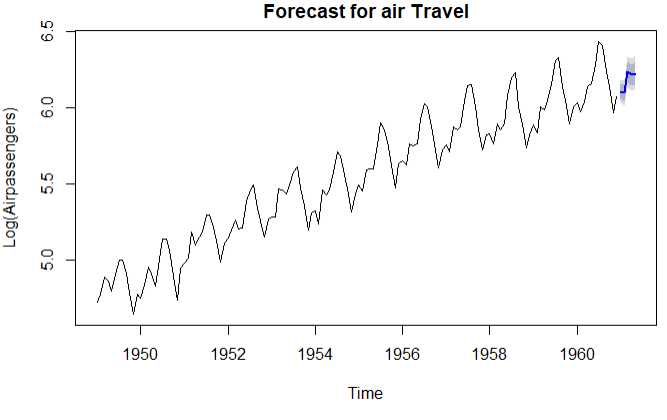

结论:从表格中可知3月份的将会有509200乘客,95%的置信区间是[454900,570000]
4.3ets自动预测
案例:自动预测JohnsonJohnson股票的趋势
1 fit4 <- ets(JohnsonJohnson) 2 fit4 3 plot(forecast(fit4),main=‘Johnson and Johnson Forecasts‘, 4 ylab="Quarterly Earnings (Dollars)", xlab="Time")
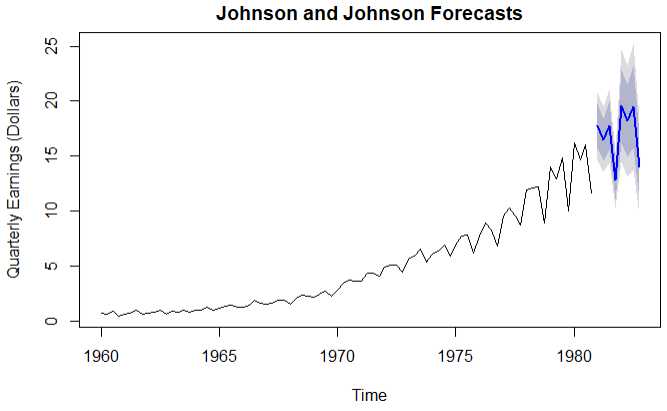
结论:预测值使用蓝色线表示,浅灰色表示80%置信空间,深灰色表示95%置信空间
5.ARIMA预测
步骤:
1.确保时序是平稳的
2.找出合理的模型(选定可能的p值或者q值)
3.拟合模型
4.从统计假设和预测准确性等角度评估模型
5.预测
library(tseries) plot(Nile) # 1.原始序列差分一次 ndiffs(Nile) dNile <- diff(Nile) # 2.差分后的图形 plot(dNile) adf.test(dNile) Acf(dNile) Pacf(dNile) # 3.拟合模型 fit5 <- arima(Nile,order = c(0,1,1)) fit5 accuracy(fit5) # 4.评价模型 qqnorm(fit5$residuals) qqline(fit5$residuals) Box.test(fit5$residuals,type = ‘Ljung-Box‘) # 5.预测模型 forecast(fit5,3) plot(forecast(fit5,3),xlab = ‘Year‘,ylab = ‘Annual Flow‘)
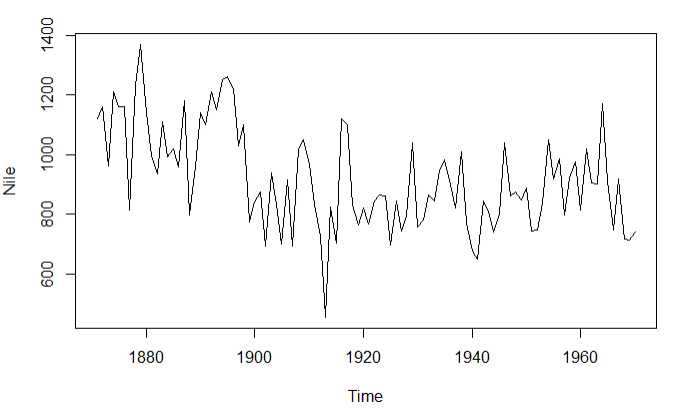
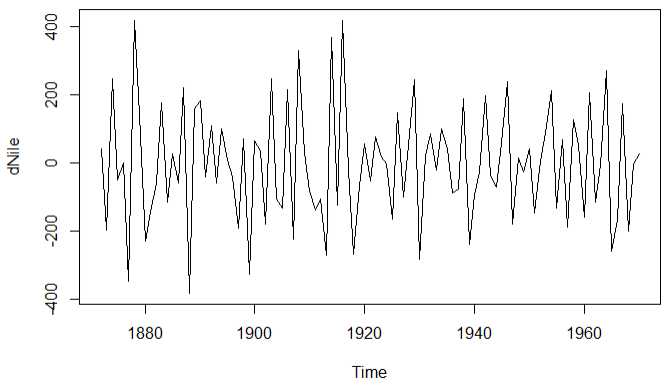
原始图 一次差分图形
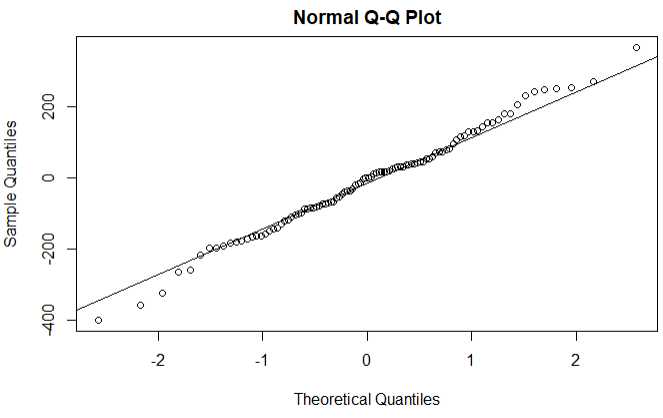
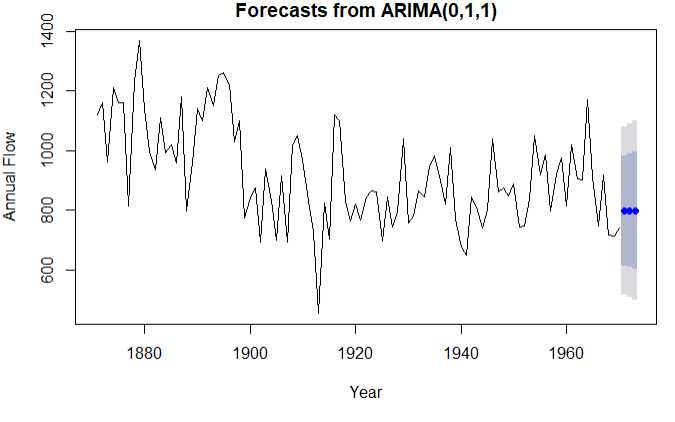
正态Q-Q图(如果满足正态分布,点会落在图中的线上) 使用Arima(0,1,1)模型的预测值
Arima自动预测
案例:预测3个月之后的太阳黑子
1 fit6 <- auto.arima(sunspots) 2 fit6 3 forecast(fit6,3) 4 accuracy(fit6) 5 plot(forecast(fit6,3), xlab = "Year", 6 ylab = "Monthly sunspot numbers")
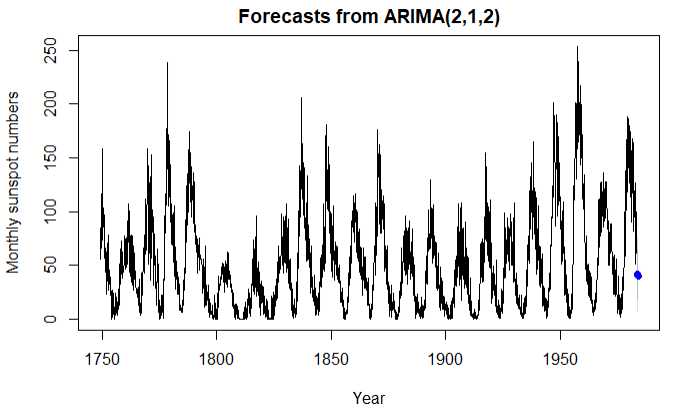
结论:函数自动选定(2,1,2)与其他模型相比,AIC的值最小,预测结果更准确
